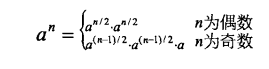【剑指offer】数值的整数次方
版权声明:本文为博主原创文章,未经博主同意不得转载。
https://blog.csdn.net/mmc_maodun/article/details/25506085
转载请注明出处:http://blog.csdn.net/ns_code/article/details/25506085
剑指offer上的第十一题,九度OJ上測试通过。
- 题目描写叙述:
-
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
- 输入:
-
输入可能包括多个測试例子。
对于每一个输入文件,第一行输入一个整数T,表示測试案例的数目。接下来的T行每行输入一个浮点数base和一个整数exponent。两个数中间用一个空格隔开。
- 输出:
-
相应每一个測试案例,
输出一个浮点数代表答案,保留两位小数就可以。
- 例子输入:
-
- 5
- 1.0 10
- 0.0 -5
- 1.0 0
- 1.2 5
- 2.0 -1
- 5
- 例子输出:
-
- 1.00e+00f
- INF
- 1.00e+00f
- 2.49e+00f
- 5.00e-01f
- 1.00e+00f
- 提示:
-
请特别注意不同的编译器对于科学计数法格式输出中指数位数的区别。
建议使用九度Online Judge所使用的编译环境。
这里採用递归求次方的方法来写代码,思路例如以下:
AC代码例如以下:
#include<stdio.h>#include<math.h>#include<stdbool.h>bool flag = true;//求base的正数absExp次幂double PowerAbs(double base,unsigned int absExp){//递归退出的条件if(absExp == 0)return 1.0;if(absExp == 1)return base;//递归求次方double result = PowerAbs(base,absExp>>1);result *= result;//推断奇偶性if(absExp&1 == 1)result *= base;return result;}//求base的exp次方double Power(double base,int exp){//底数为0。指数为负数的情况if(fabs(base-0.0)<0.0000001 && exp<=0){flag = false;return 0.0;}unsigned int absExp = (unsigned int)abs(exp);double result = PowerAbs(base,absExp);if(exp<0)result = 1.0/result;return result;}int main(){int n,exp;double base;while(scanf("%d",&n) != EOF){int i;for(i=0;i<n;i++){//每次都要先将flag置为trueflag = true;scanf("%lf %d",&base,&exp);double result = Power(base,exp);if(flag)printf("%.2ef\n",result);elseprintf("INF\n");}}return 0;}
/************************************************************** Problem: 1514 User: mmc_maodun Language: C Result: Accepted Time:80 ms Memory:912 kb****************************************************************/【剑指offer】数值的整数次方的更多相关文章
- 剑指Offer 数值的整数次方
题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 思路: 要考虑边界,0,负数 AC代码: class Solution ...
- 剑指Offer——数值的整数次方
题目描述: 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 分析: 快速幂,简单解释下, 当e的二进制为1001011, b^e=b^( ...
- 用js刷剑指offer(数值的整数次方)
题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 保证base和exponent不同时为0 牛客网链接 思路 快速幂算法,举个例 ...
- 剑指offer--6.数值的整数次方
时间限制:1秒 空间限制:32768K 热度指数:362909 题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. class S ...
- (原) 剑指offer--之数值的整数次方
题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 初次看题觉得这题好简单,直接用库函数power()不就行了,仔细想了想,万 ...
- 剑指Offer-12.数值的整数次方(C++/Java)
题目: 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 保证base和exponent不同时为0 分析: 注意base为0和expo ...
- 10-剑指offer: 数值的整数次方
题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 代码 class Solution { public: double Powe ...
- 剑指Offer09 数值的整数次方
/************************************************************************* > File Name: 09_Power. ...
- 【剑指 Offer II 001. 整数除法】同leedcode 29.两数相除
剑指 Offer II 001. 整数除法 解题思路 在计算的时候将负数转化为正数,对于32位整数而言,最小的正数是-2^31, 将其转化为正数是2^31,导致溢出.因此将正数转化为负数不会导致溢出. ...
- 剑指offer之关于整数的处理
首先是整数次方的处理 在这处理的时候有几个细节主义处理 1.当指数是负数的时候 2.当指数式0的时候 3.当不满足条件的时候要抛出异常 再一个就是常用的将一个树化为二进制的形式,或者是求整数的幂或者矩 ...
随机推荐
- Entity framework 6.0 简明教程 ef6
http://www.entityframeworktutorial.net/code-first/entity-framework-code-first.aspx Ef好的教程 Entity Fra ...
- Spring基础(1) : 自动装配
1.自动装配 1.1 byType 1.1.1根据类型自动匹配,若当前没有类型可以注入或者存在多个类型可以注入,则失败.必须要有对于的setter方法 public class Person{ pub ...
- Collection集合的带All功能的测试
public class Demo4_CollectionAll { public static void main(String[] args) { // Demo1(); // Demo2(); ...
- Codeforces675D(SummerTrainingDay06-J)
D. Tree Construction time limit per test:2 seconds memory limit per test:256 megabytes input:standar ...
- H5添加禁止缩放功能
<meta name="viewport" content="width=device-width, initial-scale=1.0, maximum-scal ...
- JavaScript--表单处理(27)
一 表单介绍 // 在HTML中,表单是由<form>元素来表示的,而在JavaScript中,表单对应的则是HTMLFormElement类型; // HTMLFormElement继承 ...
- python学习之老男孩python全栈第九期_day010知识点总结
def qqxing(l = []): # 可变数据类型 l.append(1) print(l)qqxing() # [1]qqxing([]) # [1]qqxing() # [1, 1]qqxi ...
- 随手记:tomcat 与JDK 安装与配置
写了3年的JAVA 每次遇到配置JDK 与按照tomcat的时候都要去网上找一下,太丢人了,所以还是记一下比较好,虽然都知道要配置哪些,但每次都还是有些不确定的感觉~ JDK : 1.安装官网 htt ...
- 小程序通过用户授权获取手机号之getPhoneNumber
小程序有一个获取用户很便捷的api,就是通过getPhoneNumber获取用户的已经绑定微信的手机号码.有一点要大家注意,现在微信和注重用户体验,有些方法都是需要用户主动去触发才能调用的,比如get ...
- MongoDB数据库在centos下的操作
简介 MongoDB是一个基于分布式文件存储的数据库.由C++语言编写.旨在为WEB应用提供可扩展的高性能数据存储解决方案. MongoDB是一个介于关系数据库和非关系数据库之间的产品,是非关系数据库 ...