4951: [Wf2017]Money for Nothing 决策单调性 分治

Bzoj4951:决策单调性 分治

国际惯例题面: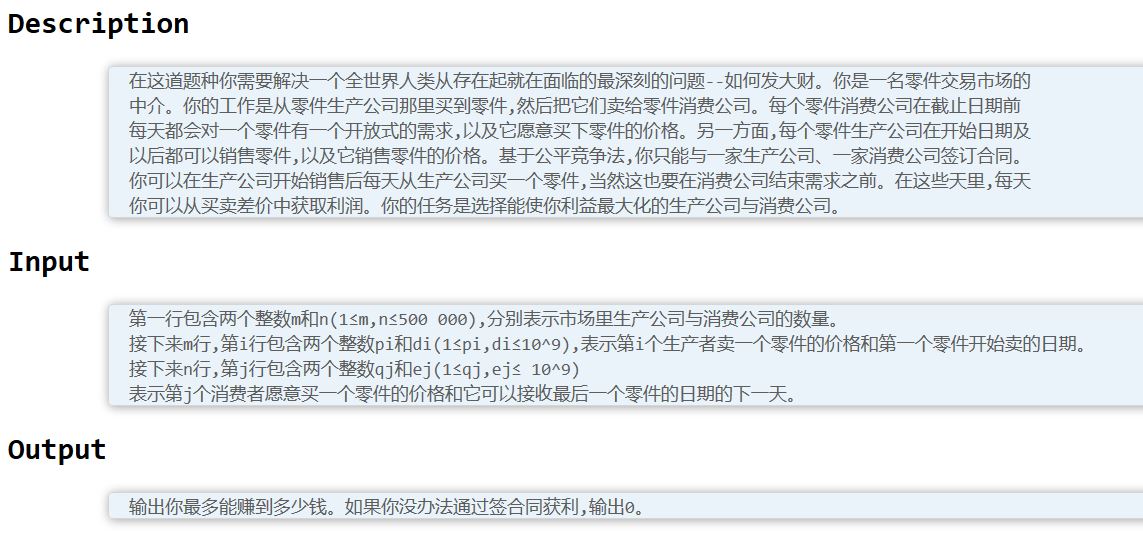

一句话题面:
供应商出货日期为Ei，售价为Pi；用户收购截止日期为Si，收购价格为Gi。我们要求max((Si-Ej)*(Gi-Pj))。
显然如果我们把这两者都按照Ei，Si递增排序，则Pi，Gi都是单调降的。
为什么？如果一个供应商生产时间后且价格高，显然你不会选择他；如果一个用户购买时间短且收购价格低，显然你也不会选择他。
然后我们会写n^2暴力了。考虑优化。

这种DP要么斜率+数据结构优化，要么就是决策单调性。
考虑斜率优化，发现这是一个三维凸包问题，不会做。
考虑决策单调性，我们猜想，对于Si递增的用户，采用的最有供货商的Ei也是单调增的。
如何证明，考虑反证法。
我们假设两个供货商出货日期为E1,E2，价格为P1,P2。
两个用户截止日期为S1,S2，收购价格为G1,G2。
不妨令E1<E2,P1>P2且S1<S2,G1>G2。
如果不满足决策单调性，我们有:
(E1-S2)*(P1-G2)>(E1-S1)*(P1-G1)
(E2-S1)*(P2-G1)>(E2-S1)*(P2-G2)
整理得:
S2*G2-S1*G1>P1*(S2-S1)+E1*(G2-G1)
P2*(S2-S1)+E2*(G2-G1)>S2*G2-S1*G1
根据不等号的传递性，我们有:
P2*(S2-S1)+E2*(G2-G1)>P1*(S2-S1)+E1*(G2-G1)
整理得:
(E2-E1)*(G2-G1)>(S2-S1)*(P1-P2)
根据我们的前提条件，E2-E1>0,G2-G1<0,S2-S1>0,P1-P2>0。
这样的话，左式((E2-E1)*(G2-G1))<0，右式((S2-S1)*(P1-P2))>0。
显然一个<0的数大于一个>0的数是不可能的，所以假设不成立，原结论成立，决策单调性得证。

然后就是代码实现的问题了，我用的是经典的分治写法，就是对于每一个用户区间的中点，找到最优供货商，然后再分离区间递归计算。
注意如果乘法的时候两边都是负数，我们应该特判掉并返回-inf(因为这个状态不合法，不能更新答案)，但是只有一边是负数的时候，我们应该计算出他的值(虽然这个状态不能更新答案，但是这个状态能更新决策)。
我一开始看到<0就返回-inf，WA了不知道多少发，身败名裂。

代码:

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 typedef long long int lli;
 const int maxn=5e5+1e2;
 const lli inf=0x3f3f3f3f3f3f3f3fll;

 struct Point {
     int x,y;
     friend bool operator < (const Point &a,const Point &b) {
         return a.x != b.x ? a.x < b.x : a.y < b.y;
     }
 }pro[maxn],usr[maxn];

 inline int fix(Point* dst,int len,bool tpe) { // tpe = 0 solve provider by pushing stack , cmp = 1 solve user by poping stack .
     static Point stk[maxn];
     std::sort(dst+,dst++len);
     int top = ;
     if( !tpe ) {
         for(int i=;i<=len;i++) if( !top || stk[top].y > dst[i].y ) stk[++top] = dst[i];
     } else {
         for(int i=;i<=len;i++) {
             while( top && stk[top].y <= dst[i].y ) --top;
             stk[++top] = dst[i];
         }
     }
     memcpy(dst+,stk+,sizeof(Point)*top);
     return top;
 }

 lli ans;

 inline lli calc(const Point &pro,const Point &usr) {
     if( usr.x < pro.x && usr.y < pro.y ) return -inf;
     return (lli) ( usr.x - pro.x ) * ( usr.y - pro.y );
 }
 inline void solve(int pl,int pr,int ul,int ur) {
     if( pl == pr || ul == ur ) {
         for(int i=pl;i<=pr;i++) for(int j=ul;j<=ur;j++) ans = std::max( ans , calc(pro[i],usr[j]) );
         return;
     }
     int pmid = pl , umid = ( ul + ur ) >> ;
     lli cur = -inf, cal;
     for(int i=pl;i<=pr;i++)
         if( ( cal = calc(pro[i],usr[umid]) ) > cur ) cur = cal , pmid = i;
     ans = std::max( ans , cur );
     if( ul < umid ) solve(pl,pmid,ul,umid-);
     if( umid < ur ) solve(pmid,pr,umid+,ur);
 }

 int main() {
     static int n,m;
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%d%d",&pro[i].x,&pro[i].y);
     for(int i=;i<=m;i++) scanf("%d%d",&usr[i].x,&usr[i].y);
     n = fix(pro,n,) , m = fix(usr,m,);
     solve(,n,,m) , printf("%lld\n",ans);
     return ;
 }

作为业界良心的我还是附送官方数据吧(Lemon格式打包):
链接：https://pan.baidu.com/s/1jbjZ6OvS5Wf5Ls46nvrRNg 密码：434d

祈る事を諦めた
我已经放弃了向神祈祷
透き通る空の朝
在那透明澄澈的清晨中
どんな気持ち抱えてても
无论怀抱着怎样的心绪
誰にも届かないなんて
也完全无法向他人传递
まるで私はエコー
仿佛只是自身在不断回响