poj4474 Scout YYF I（概率dp+矩阵快速幂）

Scout YYF I

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 4100		Accepted: 1051

Description

YYF is a couragous scout. Now he is on a dangerous mission which is to penetrate into the enemy's base. After overcoming a series difficulties, YYF is now at the start of enemy's famous "mine road". This is a very long road, on which there are numbers of mines. At first, YYF is at step one. For each step after that, YYF will walk one step with a probability of  p, or jump two step with a probality of 1- p. Here is the task, given the place of each mine, please calculate the probality that YYF can go through the "mine road" safely.

Input

The input contains many test cases ended with  EOF.
Each test case contains two lines.

The First line of each test case is 
N (1 ≤ 
N ≤ 10) and 
p (0.25 ≤ 
p ≤ 0.75) seperated by a single blank, standing for the number of mines and the probability to walk one step.

The Second line of each test case is N integer standing for the place of N mines. Each integer is in the range of [1, 100000000].

Output

For each test case, output the probabilty in a single line with the precision to 7 digits after the decimal point.

Sample Input

1 0.5
2
2 0.5
2 4

Sample Output

0.5000000
0.2500000

Source

POJ Monthly Contest - 2009.08.23, Simon

第一次接触矩阵快速幂，矩阵要专门看，快速幂单独看看

显然，如果k 号位有雷，那么安全通过这个雷只可能是在 k-1 号位选择走两步到 k+1 号位。因此，可以得到如下结论：在第 i 个雷的安全通过的概率就是从 a[i-1]+1 号位到 a[i]+1 号位的概率。于是，可以用 1 减去就可以求出安全通过第 i 个雷的概率，最后乘起来即可，比较悲剧的是数据很大，所以需要用到矩阵快速幂……

类似斐波那契数列，ans[i]=p*ans[i-1]+(1-p)*ans[i-2] ，构造矩阵为

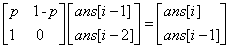
#include <iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
int s[20];
double q,p;
struct node
{
	double dp[2][2];//矩阵
};
node mult(node a,node b)//矩阵乘法
{
	int i,j,n,k;
	node temp;
	for(i=0;i<2;i++)
	{
		for(j=0;j<2;j++)
		{
			temp.dp[i][j]=0;
			for(k=0;k<2;k++)
				temp.dp[i][j]+=a.dp[i][k]*b.dp[k][j];
		}
	}
	return temp;
}
node cal(int N)//快速幂
{
	node a,res;
	a.dp[0][0]=p;
	a.dp[0][1]=q;
	a.dp[1][0]=1;
	a.dp[1][1]=0;
	res.dp[0][0]=1;
	res.dp[0][1]=0;
	res.dp[1][0]=0;
	res.dp[1][1]=1;
	while(N)
	{
		if(N&1)
		{
			res=mult(res,a);
		}
		a=mult(a,a);
		N>>=1;
	}
	return res;
}
int main()
{
    int i,j,n,m,max,flag;
    double tempqn;
	node temp,a;
    while(scanf("%d%lf",&n,&p)!=EOF)
    {
        q=1-p;
		s[0]=0;
        for(i=1;i<=n;i++)
        {
            cin>>s[i];
        }
        sort(s+1,s+1+n);
        for(i=1,flag=1;i<n;i++)
        {
            if(s[i]+1==s[i+1])
		flag=0;
        }
	if(!flag||s[1]==1)
	{
		puts("0.0000000");
continue;
	}
	a.dp[0][0]=1;
	a.dp[0][1]=0;
	a.dp[1][0]=0;
	a.dp[1][1]=0;
	for(i=1;i<=n;i++)
	{
		temp=cal(s[i]-s[i-1]-2);
		a=mult(temp,a);
		a.dp[0][0]=a.dp[0][0]*q;
		a.dp[0][1]=0;
		a.dp[1][0]=0;
		a.dp[1][1]=0;
	}
        printf("%.7f\n",a.dp[0][0]);
    }
    return 0;
}