《University Calculus》-chape6-定积分的应用-求体积
定积分一个广泛的应用就是在求解一些“看似不规则”的几何体的体积,之所以说看似不规则,是因为不规则之下还是有一定的“规则性”可言的,我们就是需要抓住这些线索进行积分运算得到体积。
方法1:切片法。

这里由于处理的方法思想和典型的离散的黎曼和到连续的积分的过程类似,因此这里不再重复推导,直接给出如何应用以及实例。
基于这条定理,我们能够直接介绍一下卡瓦列里原理。卡瓦列里原理表明,高度相同并且在每个高度上的横截面积相同的几何体的体积相同,直观的理解,就像下面这两堆“叠硬币”图。

下面我们看一些实例。
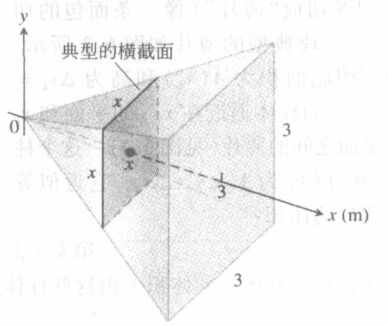
利用这种方法的计算体积具有较为严苛的限制,其中最重要的一点是,这个不规则几何体的横截面A(x)是典型的几何图形,利用这种方法计算体积能够归纳成如下的算法流程:
- 画出立体和典型的横截面草图
- 求典型横截面面积A(x)
- 求积分限
- 利用微积分基本定理求A(x)的积分
那么对于这个例子,基于草图的基础上,能够列出如下的定积分式:
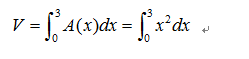
再来看一个稍微有挑战性的图。

选择横截面是有技巧的,一个关键原则是选择的这个横截面沿积分变量所在的坐标轴移动的时候,横截面需要一直保持是典型平面图形的形式。依旧将x作为积分变量,则横截面A(x)是矩形,于是我们能够列出如下的式子:
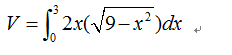
方法2:
处理旋转体的圆盘方法。
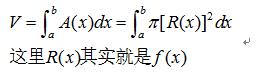
其实这种方法本质上讲是一种处理旋转体的切片法。在介绍这种方法之前,有必要先介绍一下什么是旋转体:将某平面图形绕坐标轴旋转一周形成的空间几何体我们称之为旋转体。
旋转体非常的有规律可循,假设我们旋转是曲线f(x)和x轴围成的曲边梯形,我们能够发现,将x视为积分变量,横截面处处是典型的图形——圆,而半径恰好可以通过曲线f(x)给出。
让我们看几个实例。
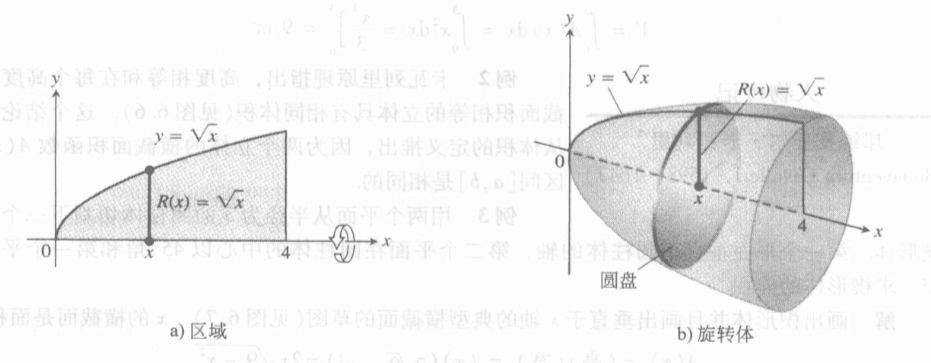
容易列出如下的定积分式。
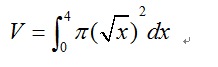
《University Calculus》-chape6-定积分的应用-求体积的更多相关文章
- 《University Calculus》-chape5-积分法-微积分基本定理
定积分中值定理: 积分自身的定义是简单的,但是在教学过程中人们往往记得的只是它的计算方法,在引入积分的概念的时候,往往就将其与计算方法紧密的捆绑在一起,实际上,在积分简单的定义之下,微积分基本定理告诉 ...
- 《University Calculus》-chaper13-多重积分-二重积分的引入
这一章节我们开始对多重积分的研究. 在此之前,我们首先来回忆起积分的过程,在平面中,面临求解不规则图形的面积(常叫曲边梯形)的时候,我们可以采取建立直角坐标系,然后通过得到不规则图形边界的函数表达式f ...
- 《University Calculus》-chape10-向量与空间几何学-向量夹角
点积.向量夹角: 无论对于空间向量还是平面向量,我们所熟知的是:给出任意两个向量,我们都能够根据公式计算它们的夹角,但是这个夹角必须是将两个向量的起点重合后所夹成的小于等于π的角,可是,这是为什么呢? ...
- 《University Calculus》-chape4-极坐标与圆锥曲线-极坐标系下的面积与弧长
极坐标系下的面积: 在直角坐标系下一样,这里在极坐标系下,我们面临一个同样的问题:如何求解一个曲线围成的面积?虽然两种情况本质上是一样的,但是还是存在一些细小的区别. 在直角坐标系下中,我们是讨论一条 ...
- 《University Calculus》-chape8-无穷序列和无穷级数-欧拉恒等式
写在前面:写在前面的当然是对大天朝教材的吐槽啦. 曾记否,高中所学虚数和复平面的概念,如此虚无的概念到了大学一门叫<模拟电子技术>的课程中居然明目张胆的开始进行计算! 曾记否,高中的指对运 ...
- 《University Calculus》-chape8-无穷序列和无穷级数-基本极限恒等式
基于基本的极限分析方法(诸多的无穷小以及洛必达法则),我们能够得到推导出一些表面上看不是那么显然的式子,这些极限恒等式往往会在其他的推导过程中用到,其中一个例子就是概率论中的极限定理那部分知识.
- 《University Calculus》-chape12-偏导数-基本概念
偏导数本质上就是一元微分学向多元函数的推广. 关于定义域的开域.闭域的推广: 其实这个定义本质上讲的就是xoy面上阴影区域的最外面的一周,只不过这里用了更加规范的数学语言. 二次函数的图形.层曲线(等 ...
- 《University Calculus》-chape3-微分法-基本概念、定理
所谓微分法其实就是我们所熟悉的导数,它是一种无限分割的方法,同积分法一样,它们是处理曲线和曲面的有利工具,也是一门很伟大的自然语言.微分方程就是一种名副其实的描述自然的语言. 同样这里如果取单侧导数, ...
- 《University Calculus》-chape6-定积分的应用-平面曲线长度
平面曲线的长度: 积分的重要作用体现在处理曲线和曲面. 在这里我们讨论平面中一条用参数形式表达的曲线:x=f(t),y=g(t),a≤t≤b. 如图. y=f(x)形式的弧长计算: 之前我们讨论过平面 ...
随机推荐
- ubuntu vim之php函数提示
参考文献:http://www.feiyan.info/32.html 折腾半天 原来是phpfunclist.txt不正确...... vim的配置在~/.vimrc (既你的home主目录 ,例如 ...
- Android中图片的异步加载
转: 1. 为什么要异步加载图片 下载图片比较费时,先显示文字部分,让加载图片的过程在后台,以提升用户体验 2. SoftReference的作用 栈内存—引用 堆内存—对象 Eg: Object ...
- php提取背景图片
preg_match_all('/background\s*-\s*+image\s*:\s*url\s*\("*([^"]*)"*\)/i', $content,$ma ...
- 记录一下学习VC的初步过程.
有需要把状态栏图标缓存清空. 找到DELPHI和E语言的例子.最近学VC所以要改成VC的. 做控件的时候发现函数不能直接控制控件.在网上找了半天相关资料,都是说要包含"resource.h& ...
- C语言实现的顺序表
顺序表是用一段地址连续的存储单元依次存储数据元素的线性结构.顺序表可分为静态存储和动态存储,静态顺序表比较简单,数据空间固定,而动态顺序表可以动态增容,便于存放大量数据,现主要把动态的基本实现一下~此 ...
- NET Portability Analyzer
NET Portability Analyzer 分析迁移dotnet core 大多数开发人员更喜欢一次性编写好业务逻辑代码,以后再重用这些代码.与构建不同的应用以面向多个平台相比,这种方法更加容易 ...
- WebComponent
WebComponent 前言 最近加入到新项目组负责前端技术预研和选型,一直偏向于以Polymer为代表的WebComponent技术线,于是查阅各类资料想说服老大向这方面靠,最后得到的结果是:& ...
- jquery 判断是否 ie6 ie7 ie8
var isIE = !!window.ActiveXObject; var isIE6 = isIE && !window.XMLHttpRequest; var isIE8 = ...
- Img图片超过了DIV的最大宽度 解决方案
在该图片所在的div限定一下里边所有的图片的最大长度,这个长度的值可以是div的长度的略小即可. 例如: <div class="content" style="w ...
- 【USACO 2012 Open】Running Laps(树状数组)
53 奶牛赛跑 约翰有 N 头奶牛,他为这些奶牛准备了一个周长为 C 的环形跑牛场.所有奶牛从起点同时起跑,奶牛在比赛中总是以匀速前进的,第 i 头牛的速度为 Vi.只要有一头奶牛跑完 L 圈之后,比 ...
