数据结构（线段树）：CodeForces 85D Sum of Medians

D. Sum of Medians

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a₁, a₂, ..., a_k}, where a₁ < a₂ < a₃ < ... < a_k, will be understood by as

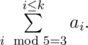
The 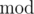operator stands for taking the remainder, that is 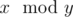stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 10⁵), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 10⁹.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

Examples

Input

6
add 4
add 5
add 1
add 2
add 3
sum

Output

3

Input

14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum

Output

5
11
13

　　这道题目不难，注意去重，还要防止爆int。

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdio>
 using namespace std;
 const int maxn=;
 int hsh[maxn],tot,Q;
 long long ans[maxn<<][];
 int sum[maxn<<],tp[maxn],num[maxn];

 void Push_up(int x){
     int l=x<<,r=x<<|;
     sum[x]=sum[l]+sum[r];
     for(int i=;i<=;i++)
         ans[x][i]=ans[l][i]+ans[r][((i-sum[l])%+)%];
 }

 void Insert(int x,int l,int r,int g,int d){
     if(l==r){
         ans[x][]+=hsh[l]*d;
         sum[x]+=d;
         return;
     }
     int mid=(l+r)>>;
     if(mid>=g)Insert(x<<,l,mid,g,d);
     else Insert(x<<|,mid+,r,g,d);
     Push_up(x);
 }

 char op[];
 int main(){
     scanf("%d",&Q);
     for(int q=;q<=Q;q++){
         scanf("%s",op);
         if(op[]=='a')tp[q]=;
         else if(op[]=='d')tp[q]=-;
         else continue;
         scanf("%d",&num[q]);
         if(tp[q]==){++tot;hsh[tot]=num[q];}
     }

     sort(hsh+,hsh+tot+);
     tot=unique(hsh+,hsh+tot+)-hsh-;

     for(int q=;q<=Q;q++){
         if(tp[q]==){
             int p=lower_bound(hsh+,hsh+tot+,num[q])-hsh;
             Insert(,,tot,p,);
         }
         else if(tp[q]==-){
             int p=lower_bound(hsh+,hsh+tot+,num[q])-hsh;
             Insert(,,tot,p,-);
         }
         else
             printf("%I64d\n",ans[][]);
     }
     return ;
 }