洛谷P4180【Beijing2010组队】次小生成树Tree

题目描述:

小C最近学了很多最小生成树的算法，Prim算法、Kurskal算法、消圈算法等等。正当小C洋洋得意之时，小P又来泼小C冷水了。小P说，让小C求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说：如果最小生成树选择的边集是$E_M$，严格次小生成树选择的边集是$E_S$，那么需要满足：($value(e)$表示边e的权值)

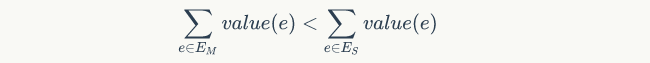
这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。

输入输出格式:

输入格式:

第一行包含两个整数N和M，表示无向图的点数与边数。接下来M行，每行3个数 x y z 表示，点x和点y之间有一条边，边的权值为z。

输出格式:

包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)

输入输出样例:

输入样例:

1 2 3 4 5 6 7

5 6 1 2 1 1 3 2 2 4 3 3 5 4 3 4 3 4 5 6

输出样例:

1

11

说明:

数据中无向图无自环
50%的数据$N≤2000,;M≤3000$
80%的数据$N≤50000,;M≤100000$
100%的数据$N≤100000,;M≤300000$, 边权值非负且不超过$10^9$。

SOL:

首先求出最小生成树，然后将最小生成树的边依次断开，换成指定的一条边，
求出这个环中最长的一条边，换掉即可。

Code:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155

#include<bits/stdc++.h> #define RG register #define file(x) freopen(#x".in", "r", stdin);freopen(#x".out", "w", stdout); #define for_edge(i, x) for(RG int i=head[x];i;i=e[i].next) #define clear(x, y) memset(x, y, sizeof(x)); using namespace std; template<typename T> inline T read() { T data=0, w=1; char ch=getchar(); while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar(); if(ch=='-') w=-1, ch=getchar(); while(ch>='0'&&ch<='9') data=(data<<3)+(data<<1)+(ch^48), ch=getchar(); return data*w; } const int maxn(100010), maxm(300010); struct edge { int next, to; long long dis; } e[maxn << 1]; int head[maxn], e_num; inline void add_edge(int from, int to, long long dis) { e[++e_num]={head[from], to, dis}; head[from]=e_num; } struct edge_k { int from, to; long long dis; } edg[maxm]; inline bool cmp(const edge_k &a, const edge_k &b) { return a.dis<b.dis; } int fa[ma 大专栏  洛谷P4180【Beijing2010组队】次小生成树Treexn], n, m; long long value; bool use[maxm]; inline int find(const int &x) { return fa[x] == x ? x : fa[x]=find(fa[x]); } inline void mst() { long long ans=0; for(RG int i=1;i<=n;i++) fa[i]=i; for(RG int i=1;i<=m;i++) { int x=find(edg[i].from), y=find(edg[i].to); if(x!=y) { fa[max(x, y)]=min(x, y); ans+=edg[i].dis; use[i]=true; add_edge(edg[i].from, edg[i].to, edg[i].dis); add_edge(edg[i].to, edg[i].from, edg[i].dis); } } value = ans; } long long fst[maxn][18], sec[maxn][18], ANS=0; int f[maxn][18], deep[maxn]; inline void dfs(int x) { for_edge(i, x) { int to=e[i].to; long long ds=e[i].dis; if(to==f[x][0]) continue; f[to][0]=x; fst[to][0]=sec[to][0]=ds; deep[to]=deep[x]+1; dfs(to); } } inline void get_sec(long long &sec, long long a, long long b, long long c, long long d, long long _max) { if(a<_max) sec=a; if(b<_max) sec=max(sec, b); if(c<_max) sec=max(sec, c); if(d<_max) sec=max(sec, d); } inline void init() { dfs(1); for(RG int j=1;j<18;j++) for(RG int i=1;i<=n;i++) { f[i][j]=f[f[i][j-1]][j-1]; long long f1=fst[i][j-1], f2=fst[f[i][j-1]][j-1], s1=sec[i][j-1], s2=sec[f[i][j-1]][j-1]; fst[i][j]=max(f1, f2); get_sec(sec[i][j], f1, f2, s1, s2, fst[i][j]); } } inline long long query(int a, int b, long long dis) { if(deep[a]<deep[b]) swap(a, b); long long fsa=-1, sca=-1, fsb=-1, scb=-1; int d=deep[a]-deep[b]; for(RG int i=0;(1<<i)<=d;i++) { if((1<<i)&d) { long long tmp=sca; get_sec(sca, fsa, fst[a][i], tmp, sec[a][i], max(fsa, fst[a][i])); fsa=max(fsa, fst[a][i]); a=f[a][i]; } } if(a==b) { long long tmp=sca; get_sec(sca, fsa, fsb, tmp, scb, max(fsa, fsb)); if(dis==max(fsa, fsb)) return value-sca+dis; else return value-max(fsa, fsb)+dis; } for(RG int i=17;~i;i--) { if(f[a][i]!=f[b][i]) { long long tmp=sca; get_sec(sca, fsa, fst[a][i], tmp, sec[a][i], max(fsa, fst[a][i])); fsa=max(fsa, fst[a][i]); a=f[a][i]; tmp=scb; get_sec(scb, fsb, fst[b][i], tmp, sec[b][i], max(fsb, fst[b][i])); fsb=max(fsb, fst[b][i]); b=f[b][i]; } } long long tmp=sca; get_sec(sca, fsa, fst[a][0], tmp, sec[a][0], max(fsa, fst[a][0])); fsa=max(fsa, fst[a][0]); a=f[a][0]; tmp=scb; get_sec(scb, fsb, fst[b][0], tmp, sec[b][0], max(fsb, fst[b][0])); fsb=max(fsb, fst[b][0]); b=f[b][0]; tmp=sca; get_sec(sca, fsa, fsb, tmp, scb, max(fsa, fsb)); if(dis==max(fsa, fsb)) return value-sca+dis; else return value-max(fsa, fsb)+dis; } const long long I(9223372036854775807ll); int main() { n=read<int>(); m=read<int>(); for(RG int i=1;i<=m;i++) edg[i].from=read<int>(), edg[i].to=read<int>(), edg[i].dis=read<long long>(); sort(edg+1, edg+m+1, cmp); mst(); init(); ANS=I; for(RG int i=1;i<=m;i++) if(!use[i]) ANS=min(ANS, query(edg[i].from, edg[i].to, edg[i].dis)); printf("%lldn", ANS); return 0; }