题目分享L
题意:n个人围成一个环,每个人初始有一些金币,每个人可以把金币递给相邻的人,问最少传递多少金币使每个人金币数相同?
分析:首先在保证最优的情况下不可能会出现相邻的两个人互相送金币,因为这样他们公共的部分等于没送,那么我们就可以用bi来表示i号人往左边送的金币,可以为负,为负就表示左边送回来,那么,如果设p为金币相等时每人的金币数(总金币的平均数),ai为i号人原始的金币数,那么很容易得到:
a1-b1+b2=p
a2-b2+b3=p
……
an-bn+b1=p
而我们要求的是bi的绝对值之和,所以再转化一下
b2=p-a1+b1
b3=p-a2+b2
……
bn=p-an+bn-1
然后将所有右试中b2-bn-1代换为b1即
b2=p-a1+b1
b3=p-a2+(p-a1+b1)=p-a1+p-a2+b1
……
bn=p-a1+p-a2+……+p-an-1+b1
而p,a1-an都是常数,输入都给了,所以我们把它写成c使我们看起来方便一些
|b1|=|b1| //这里也可以写成 |b1|=|b1-c1| ,c1=0
|b2|=|b1-c2| ,c2=a1-p
|b3|=|b1-c3| ,c3=a1-p+a2-p
……
|bn|=|b1-cn| ,cn=a1-p+a2-p+……+an-1-p
为什么要写成b1-ci的形式呢?
因为|a-b|相当于在数轴上a与b的距离
所以最终的结果是 |b1| + |b2| + |b3| + …… + |bn| =|b1-c1| + |b2-c2| + …… + |bn-cn|
而只有b1是未知数,所以其实最终结果就是在数轴上离c1,c2,……,cn距离之和的最小值
而这应该初中的时候都学过
将这n个点在数轴上表示出来
这时的c1-cn我将它看做原c数组从小到大排完序后的数组
那么显然为了保证|b1-c1|+|b1-cn|的值最小,b1应该在c1-cn之间
为保证|b1-c2|+|b1-cn-1|的值最小,b1应该在c2-cn-1之间
……
最后如果n是偶数的话,b1取cn/2到cn/2+1之间的值都可以
如果n是奇数的话,b1只能取c(n+1)/2
为了方便我们之间让b1=c(n+1)/2就可以了
这里求c(n+1)/2可以用nth_element() O(n) 有兴趣可以去cplusplus学一下,当然sort也是可以的
最后将b1的值带去原式子中计算就行
代码: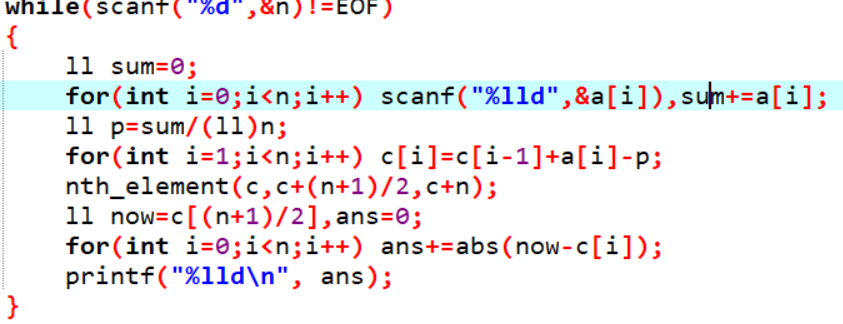
题目分享L的更多相关文章
- 题目分享C 二代目
题意:一个数列是由 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6.....组成,也就是1-1,1-2,1-3......并且如果遇到多位数也要拆成数字比如1-10 ...
- 题目分享X
题意:一张票有n位数,如果这张票的前一半数字的和等于后一半数字的和(n一定是偶数),就称这张票为快乐票.有些数被擦除了,标记为’?’(’?‘的个数也是偶数),现在Monocarp 和 Bicarp 进 ...
- 2019年腾讯PHP程序员面试题目分享
有需要学习交流的友人请加入交流群的咱们一起,有问题一起交流,一起进步!前提是你是学技术的.感谢阅读! 点此加入该群jq.qq.com 1. php 的垃圾回收机制 PHP 可以自动进行内存管理,清除 ...
- 20190924-LeetCode解数独题目分享
解决数独 题目描述 编写一个程序,通过已填充的空格来解决数独问题. 一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次. 数字 1-9 在每一列只能出现一次. 数字 1-9 在每一个以 ...
- 题目分享H 二代目
题意:有m个限制,每个限制l1,r1,l2,r2四个数,限制了一个长度为n的数第l1到r1位要与第l2到r2相同,保证r1-l1=r2-l2,求在限制下一共有多少种数 分析: 暴力的话肯定是从l1-r ...
- 题目分享E 二代目
题意:一棵点数为n的树,每个节点有点权,要求在树中中找到一个最小的x,使得存在一个点满足max(该点点权,该点相邻的点的点权+1,其他点的点权+2)=x 分析:首先要能把题目转化为上述题意 首先题目让 ...
- 题目分享D 二代目
题意:给定一个T条边的无向图,求S到E恰好经过N条边的最短路径 T≤100 N≤1000000 分析:(据说好像假期学长讲过) 首先很容易想到的是dp[i][j][k]表示从i到j经过k条边的最短路径 ...
- 题目分享V
题意:现在两个人做游戏,每个人刚开始都是数字1,谁赢了就能乘以k^2,输的乘以k(k可以是任意整数,每次不一定相同)现在给你最终这两个人的得分,让你判断是否有这个可能,有可能的话Yes,否则No. 分 ...
- 题目分享T
题意:蛐蛐国里现在共有n只蚯蚓(n为正整数).每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为a_i(i=1,2,...,n),并保证所有的长度都是非负整数(即:可 能存在长度为0的蚯蚓).每一秒,神刀手会 ...
随机推荐
- springboot httpsession.getAtt....is null
1.开始怀疑是 @RequestMapping("") public String loginIndex() { return "admin/login"; } ...
- vue(element)中使用codemirror实现代码高亮,代码补全,版本差异对比
vue(element)中使用codemirror实现代码高亮,代码补全,版本差异对比 使用的是vue语言,用element的组件,要做一个在线编辑代码,要求输入代码内容,可以进行高亮展示,可以切换各 ...
- mysql命令行参数 --- 这些参数不同于 mysqldump 后的 那些参数(下边文章开头有链接) :2种类型的参数 含义是不一样的
mysql命令行参数 --- 这些参数不同于 mysqldump 后的 那些参数 :2种类型的参数 含义是不一样的 一,mysql命令行参数 Usage: mysql [OPTIONS] [ ...
- uni-app同步缓存值 设置 读取 删除
A页面 <view class="go-to-tab" @tap="gotologin"> 去login页面 </view> msg : ...
- webWMS开发过程记录(六)- 详细设计之系统管理
一.功能说明 1. 权限管理 (参考“权限管理-百度百科") 定义:一般指根据系统设置的安全规则或安全策略,用户可以访问而且只能访问自己被授权的资源,不多不少. 分类:从控制力度来看,通常分 ...
- 你知道如何自动保存 Spring Boot 应用进程号吗
1. 前言 欢迎阅读 Spring Boot 2 实战 系列文章. PID 对于系统运维来说并不陌生,但是对于一些开发者特别是新手还是要简单介绍一下的.它是 Process ID 的简称,是系统分配给 ...
- cucumber学习索引
Cucumber(1) —— 环境配置 Cucumber(2)——目录结构以及基本语法 Cucumber(3)——命令以及日志 Cucumber(4)——jenkins的集成
- Linux学习笔记(八)权限管理命令
权限管理命令 权限位含义 chmod chown chgrp umask默认权限 权限位含义 第1位代表文件类型 "-":普通文件 "b":块设备文件 &quo ...
- 嵌入css方式
总体见思维导图 . 嵌入css方式 1 内联式 内联式css样式表就是把css代码直接写在现有的HTML标签中,如下面代码: <p style="color:red"> ...
- [git] github上传项目(使用git)、删除项目、添加协作者
来源:http://www.cnblogs.com/sakurayeah/p/5800424.html (怕链接失败,所以直接就就复制过来啦,感谢作者) 一.注册github账号 github网址ht ...
