Pop Sequence 题解

Pop Sequence（PAT）

https://www.nowcoder.com/pat/5/problem/4090

前言：

PAT上一道Stack的应用题，简化版的有《信息学一本通·普及篇》的车厢调度

题目简述：

输入依次给定三个不大于1000的整数：m,n,k

其中m是栈的最大长度，有n个元素，进行k种出栈猜测

以下k行，输入出栈猜测，针对每种猜测，判断是否可行，可行则输出“YES”，反之输出“NO”

---

思路：

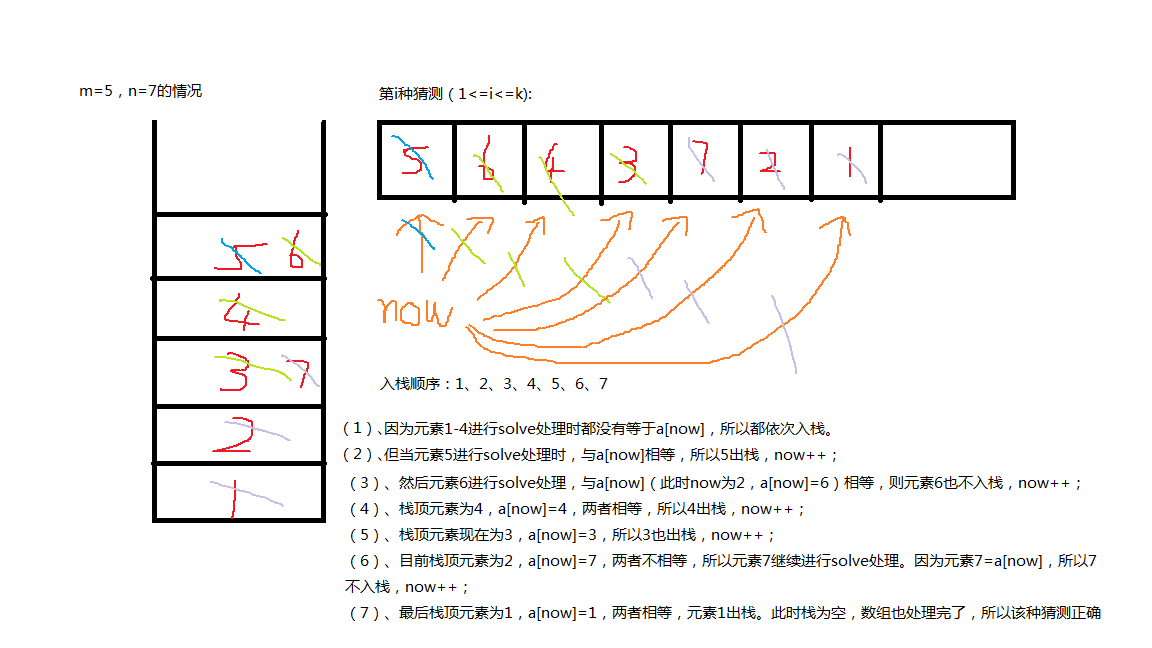
将每次给定的出栈猜测当做数组a，然后将元素从1-n依次进行入栈再进行solve处理。

处理规则：

（1）、设数组当前下标为now。从a[1]-a[now]判断a[i]是否等于栈顶元素，如果有，则弹出当前元素，并将a[i]标记为用过；如果不等于，则跳出循环不考虑后面的a[i]（联系栈的特征“后进先出”——上面出去下面才能出去，便于理解）

（2）、如果当前栈的size超过了m，则说明栈满了，直接打标记最后输出“NO”

（3）、所有solve处理完后，判断当前栈是否为空，如果为空则说明第i种出栈猜测（1<=i<=k）正确，输出“YES”；如果不为空则说明不正确，输出“NO”

因为感觉自己没有讲得很清楚，现在给出草图帮助大家理解（如果还不是很清楚，可以结合代码哦qwq）

---

代码Code：

#include <bits/stdc++.h>
using namespace std;
int n,m,k,a[1001],b[1001];
stack<int> num;

inline int solve(int now,int last) {
	int lasts=last; //相当于标记哪些i用过
	for(register int i=last;i<=now;i++) {
		if(num.empty()) break; //如果为空直接跳出
		if(num.top()==a[i]) { //相等就弹出栈，并标记当前i用过
			lasts++;
			num.pop();
		}
		else break; //因为是栈，所以不相等就跳出
	}
	return lasts;
}

int main() {
	scanf("%d%d%d",&m,&n,&k);
	for(register int i=1;i<=k;i++) {
		int start=1;
		bool p=true; //标记是否size>m
		for(register int j=1;j<=n;j++) {
			scanf("%d",&a[j]); //输入一个就处理一个
			num.push(j);
			if(num.size()>m) p=false;
			else start=solve(j,start);
		}
		//cout<<num.size()<<" ";
		if(!num.empty()||p==false) puts("NO");
		else puts("YES");
		while(!num.empty()) num.pop(); //因为是多种操作，所以记得清空
	}
	return 0;
}

---

再讲一下简化版的车厢调度吧，因为只有一种猜测，所以程序只需要主程序更改一点就可以A掉，主程序如下：

int main() {
	scanf("%d",&n);
	int start=1;
	bool p=true;
	for(register int j=1;j<=n;j++) {
		scanf("%d",&a[j]);
		num.push(j);
		start=solve(j,start);
	}
	if(!num.empty()||p==false) puts("NO");
	else puts("YES");
	return 0;
}

---