ODEINT 求解常微分方程（1）

An example of using ODEINT is with the following differential equation with parameter k=0.3, the initial condition y0=5 and the following differential equation.

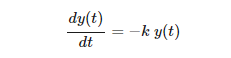
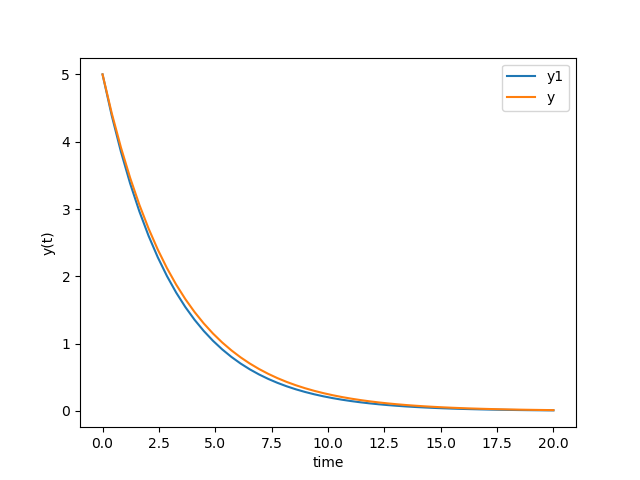
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dy/dt
def model(y,t):
    k = 0.3
    dydt = -k * y
    return dydt

# initial condition
y0 = 5

# time points
[t,dt] = np.linspace(0,20,retstep=True)

# solve ODE
y = odeint(model,y0,t)

# another way to do
y1=np.empty_like(t)
y1[0]=y0

for i in range(len(t)-1):
    y1[i+1]=y1[i]+dt*model(y1[i],t)

# plot results
plt.plot(t,y1,label='y1')
plt.plot(t,y,label='y')
plt.xlabel('time')
plt.ylabel('y(t)')
plt.legend(loc='best')
plt.show()