numpy ndarray可用的常规函数

该部分位于numpy - ref - 1.14.5中的2.8 available ufuncs

1 数学运算

1.1 元素级加法 add

加法规则：

numpy.add(x1, x2, /, out=None, *, where=True, casting=’same_kind’, order=’K’, dtype=None, subok=True[, signature, extobj]) = <ufunc 'add'>

x1 ，x2 - number，ndarray，Iterable 均可，实际上一般为ndarray。

out - 存储结果的位置，如果提供，其必须事具有输入广播的形状，如果无或者不提供，则返回新分配的数组；元组（可能仅作为关键字参数）的长度必须等于输出的数量。

余下参数略，不做说明，实际上记住 numpy.add(x1, x2） 即可，余下参数用的不多

示例一：一个ndarray + 数字

将数字与ndarray中的每一个元素相加

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.add(a,2)
print(b)
# [[3 4]
#  [5 6]]

示例二：两个同shape的ndarray相加

对应元素相加

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.arange(0,4).reshape(2,2)
print(b)
# [[0 1]
#  [2 3]]
c = np.add(a,b)
print(c)
# [[1 3]
#  [5 7]]

示例三：两个shape不全相等的ndarray相加

此时相当于 广播

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.arange(0,2)
print(b)
# [0 1]
c = np.add(a,b)
print(c)
# [[1 3]
#  [3 5]]

示例四：两个shape不全相等的ndarray相加

此时 与 广播 等价

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.arange(0,2).reshape(-1,1)
print(b)
# [[0]
#  [1]]
c = np.add(a,b)
print(c)
# [[1 2]
#  [4 5]]

示例五：两个shape不全相等的ndarray相加

此时相当于广播

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.arange(0,4).reshape(1,2,2)
print(b)
# [[[0 1]
#   [2 3]]]
c = np.add(a,b)
print(c)
# [[[1 3]
#   [5 7]]]

示例六：x1 x2的shape值不符合广播规则时，无法add

numpy 广播

a = np.arange(1,5).reshape(2,2)
print(a)
# [[1 2]
#  [3 4]]
b = np.arange(0,4)
print(b)
# [0 1 2 3]
c = np.add(a,b)
print(c)
# ValueError: operands could not be broadcast together with shapes (2,2) (4,) 

a = np.arange(1,7).reshape(2,3)
print(a)
# [[1 2 3]
#  [4 5 6]]
b = np.arange(0,4).reshape(2,2)
print(b)
# [[0 1]
#  [2 3]]
c = np.add(a,b)
print(c)
# ValueError: operands could not be broadcast together with shapes (2,3) (2,2) 

综上：当x1.shape != x2.shape 时，x1 x2 必须可广播到一个通用形状（可能是其中一个或另一个形状shape）they must be broadcastable to a common shape (which may be the shape of one or the other)。

1.2 元素级减法 subtract(x1, x2)

相减，该算法与加法相似，略

1.3 元素级乘法 multiply(x1,x2)

乘法，示例

# a = np.arange(1,5).reshape(2,2)
a = np.arange(1,5)
print(a)
# [1 2 3 4]
b = np.arange(0,4).reshape(-1,1)
print(b)
# [[0]
#  [1]
#  [2]
#  [3]]
c = np.multiply(a,b)
print(c)
# [[ 0  0  0  0]
#  [ 1  2  3  4]
#  [ 2  4  6  8]
#  [ 3  6  9 12]]

1.4 元素级除法 divide(x1, x2)、floor_divide(x1, x2)、floor_divide(x1, x2)

a = np.arange(1,5)
print(a) #[1 2 3 4]

b = np.divide(a,2)
print(b)
# [0.5 1.  1.5 2. ]

c = np.true_divide(a,2)
print(c)
# [0.5 1.  1.5 2. ]

d = np.floor_divide(a,2)
print(d)
# [0 1 1 2]

print(a/2)
# [0.5 1.  1.5 2. ]

print(a//2)
# [0 1 1 2]

注解：

（1）divide(x1, x2)、  true_divide、 / 是等价的，为真除

（2）floor_divide(x1, x2) 、// 是等价的，为地板除

1.5 元素级 幂指数和的对数计算 logaddexp(x1, x2)、logaddexp2(x1, x2)

logaddexp(x1, x2) 等价于 log(exp(x1) + exp(x2)) ，

logaddexp2(x1, x2) 等价于 log2(2**x1 + 2**x2)

该函数在统计学方面是非常有用的，其计算的时间概率非常小，甚至超过了正常浮点数的范围。

a = np.arange(0,3)
print(a)
# [0 1 2]
b = np.arange(1,4)
print(b)
# [1 2 3]
c = np.logaddexp(a,b)
print(c)
# [1.31326169 2.31326169 3.31326169]

1.6 元素级 指数函数exp(x)、exp2(x)、expm1(x)

exp(x) - 计算所有元素的对数（以自然对数 e - 2.718281为底）

exp2(x) - 计算所有元素的对数（以2为底）

expm(x) - 计算数组中所有元素的 exp(x) - 1

a = np.arange(0,3)
print(a)
# [0 1 2]

b = np.exp(a)
print(b)
# [1.         2.71828183 7.3890561 ]

c = np.expm1(a)
print(c)
# [0.         1.71828183 6.3890561 ]

d = np.exp2(a)
print(d)
# [1. 2. 4.]

1.7 元素级 自然对数 log(x)、log2(x)、log10(x)、log1p(x)

log(x) - 自然对数，以自然数e为底的x的对数

log2(x) - 2为底的对数

log10(x) - 10为底的对数

log1p(x) - 计算 log(1 + x).

a = np.arange(0,3)
print(a)
# [0 1 2]

b = np.exp(a)
print(b)
# [1.         2.71828183 7.3890561 ]

c = np.log(b)
print(c)
# [0. 1. 2.]

d = np.log1p(b)
print(d)
# [0.69314718 1.31326169 2.12692801]

 

1.8 相反数negative(x)

取x的相反数，类似函数 y = -x

a = np.array([0,-1,2,-3)
b = np.negative(a)
print(b)
# [ 0 1 -2 3]

1.9 positive(x)

返回 y (= +x) ，略

1.10 元素级 幂 power(x1, x2)

类似函数 y = x1 ** x2 ，

第一个array elements x1 raised to powers 从第二个 array 中

a = range(6)
print(a)
# range(0, 6)

b = np.power(a,2)
print(b)
# [ 0  1  4  9 16 25]

示例二

a = range(6)
print(a)
# range(0, 6)

b = [6.0, 5.0, 4.0, 3.0, 2.0, 1.0]
c = np.power(a,b)
print(c)
# [ 0.  1. 16. 27. 16.  5.]

示例三（the effect of broadcasting 广播的作用）

a = range(6)
print(a)
# range(0, 6)

b = np.array([[6, 5, 4, 3, 2, 1], [6, 5, 4, 3, 2, 1]])
c = np.power(a,b)
print(c)
# [[ 0  1 16 27 16  5]
#  [ 0  1 16 27 16  5]]

1.11 余数remainder(x1, x2)

示例一

a = np.array([1,2,3,4])
c = np.remainder(a,2)
print(c)
# [1 0 1 0]

示例二

a = np.remainder([4,7],[2,3])
print(a) #[0 1]

对于余数，其实 remainder() 余数计算是 floor_divide() 的地板除计算的 complementary。

示例三

a = np.remainder(
    [4, 7, -7, 7, -7],
    [2, 3, 3, -3, -3]
#   [0  1  2  -2  -1] a的值
)
print(a)

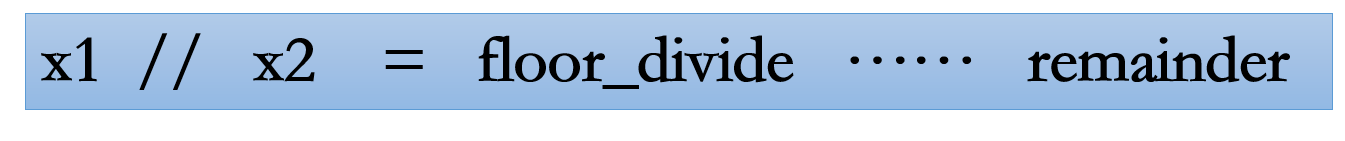
1.12 模运算mod(x1, x2)、fmod(x1, x2)、divmod(x1,x2)

mod(x1, x2) - mod函数与remainder函数的功能完全一致

fmod(x1, x2) - fmod函数所得余数值得正负由被除数决定，与除数得正负无关，此与mod、remainder、%处理负数的方式不同。

a = np.mod(
    [4, 7, -7, 7, -7],# 被除数
    [2, 3, 3, -3, -3] # 除数
#   [0  1  2  -2  -1] mod 余数正负由被除数 除数一起决定
)
print(a)

b = np.fmod(
    [4, 7, -7, 7, -7], # 被除数
    [2, 3, 3, -3, -3]  # 除数
#   [0  1  -1  1  -1]  fmod余数正负由被除数决定，与除数正负无关
)
print(b)

divmod(x1,x2) - 函数所得余数正负与 mod 函数相同，其会返回一个包含 floor_divide 和 mod 的元组，

a = np.divmod(
    [4, 7, -7, 7, -7],# 被除数
    [2, 3, 3, -3, -3] # 除数
#   (array([ 2,  2, -3, -3,  2], dtype=int32),该结果值与floor_divide类似
#    array([ 0,  1,  2, -2, -1], dtype=int32)) 该结果值与mod类似
)
print(a)

1.13 绝对值 absolute(x)、fabs(x)

absolute(x) - 绝对值（返回值为整型）

fabs(x) - 绝对值（返回值浮点类型）

a = np.array([0,-1,2,-3,4])
b = np.absolute(a)
print(b) #[0 1 2 3 4]

c = np.fabs(a)
print(c) # [0. 1. 2. 3. 4.]

1.14 四舍五入 rint(x)

将数组中的元素舍入到最接近的整数。

a = np.array([1.4, 1.5, 1.6, 2.4, 2.5, 2.6])
c = np.rint(a)
print(c)   # [ 1.  2.   2.   2.   2.   3.]

四舍五入：四舍六入五留双

1.15 数学标志符号 sign(x)

返回一个数字符号的元素指示

对于实数而言

x < 0    return   -1

x == 0  return    1

 x > 0    return    1

 

对于虚数 complex 而言

x.real  !=  0    return sign( x.real ) + 0 j

x.real == 0     return sign( x.imag ) + 0 j

注：real为实部，imag为虚部

a = np.array([-5,5])
b = np.sign(a)
print(b)#[-1  1]

c = np.sign(5-2j)
print(c)#(1+0j)

d = np.sign(-2j)
print(d)#(-1+0j)

1.16 分段函数 heaviside(x1, x2)

                    0   if x1 < 0
heaviside(x1, x2) = x2  if x1 == 0
                    1   if x1 > 0 

示例：

a = np.heaviside([-1.5, 0, 2.0], 0.5)
print(a)# [0.  0.5 1. ]

a = np.heaviside([-1.5, 0, 2.0], 1)
print(a) # [0. 1. 1.]

1.17 复共轭 conj(x)

复数的复共轭是通过改变其虚部的符号来获得的。

a = np.conjugate(2+2j)
print(a)# (2-2j)

1.18 算术平方根sqrt(x)、立方根 cbrt(x)

a = np.arange(0,4)
print(a)
# [0 1 2 3]

b = np.sqrt(a)
print(b)
# [0. 1. 1.41421356 1.73205081]

c = np.cbrt([0,1,8,27])
print(c)
# [0. 1. 2. 3.]

1.19 平方 square(x)

a = np.square([0,1,2,3])
print(a)
# [0 1 4 9]

1.20 倒数 reciprocal(x)

a = np.reciprocal([1,2,3])
print(a)
# [1 0 0]

b = np.reciprocal([1.,2.,3.])
print(b)
# [1.  0.5   0.33333333]

备注，倒数与原数的数据类型一致。