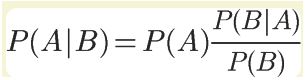ML(3): 贝叶斯方法

对于分类问题，我们每个人每天都在执行分类操作，只是我们没有意识到罢了。例如，当你看到一个陌生人，你的脑子下意识判断TA是男是女；你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱、那边有个非主流”之类的话，其实这就是一种分类操作。为更好理解Bayes原理，转载参考下面的文章：

① http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html

② http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

目录：

• 贝叶斯定理
• 全概率公式
• 贝叶斯推断的含义
• 朴素贝叶斯分类的原理

贝叶斯定理

---

      贝叶斯定理（Bayes' theorem）是英国数学家托马斯·贝叶斯（Thomas Bayes）在1763年发表的一篇论文中提出的，它是贝叶斯推断的应用。贝叶斯推断（Bayesian inference）是一种统计学方法，用来估计统计量的某种性质。 贝叶斯定理实际上就是计算"条件概率"的公式。

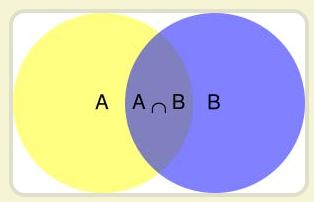
     "条件概率"（Conditional probability）: 就是指在事件B发生的情况下，事件A发生的概率，用P(A|B)来表示。

• 

根据文氏图，可以很清楚地看到在事件B发生的情况下，事件A发生的概率就是P(A∩B)除以P(B)

全概率公式

---

假定样本空间S，是两个事件A和A'的和

• 

上图中，红色部分是事件A，绿色部分是事件A'，它们共同构成了样本空间S。这种情况下，事件B可以划分为两个部分。

• 

这就是全概率公式。它的含义是：如果A和A‘构成样本空间的一个划分，那么事件B的概率，就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。将这个公式代入上一节的条件概率公式，就得到了条件概率的另一种写法：

• 

贝叶斯推断的含义

---

   对条件概率公式进行变形，可以得到如下形式：

• 

把P(A)称为”先验概率“，即在B事件发生之前，我们对A事件概率的一个判断。P(A|B)称为”后验概率“，即在事件B发生之后，我们队A事件的重新评估。P(B|A)/P(B)称为”可能性函数“，这是一个调整因子，使得预估概率更接近真实概率。所以，条件概率可以理解为下面的式子：

• 

这就是贝叶斯推断的含义。我们先预估一个”先验概率“，然后加入实验结果，看这个实验到底是增强还是消弱了”先验概率“，由此得到更接近事实的”后验概率“。
  在这里，如果”可能性函数“P(B|A)/P(B)>1，意味着”先验概率“增强，事件A的发生的可能性变大；如果”可能性函数“P(B|A)/P(B)=1，意味着B事件无助于事件A的可能性；如果”可能性函数“P(B|A)/P(B)<1，意味着”先验概率“被消弱，事件A发生的可能性变小。

水果糖问题示例

---

为了加深对贝叶斯推断的理解，我们看下面例子

• 

两个一模一样的碗，一号碗有30颗水果糖和10颗巧克力糖，二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗，从中摸出一颗糖，发现是水果糖。请问这颗水果糖来自一号碗的概率有多大？
    我们假定，H1表示一号碗，H2表示二号碗。由于这两个碗是一样的，所以P(H1)=P(H2)，也就是说，再取出水果糖之前，这两个碗被选中的概率相同。因此，P(H1)=0.5，我们把这个概率叫做”先验概率“，即没有做实验之前，来自一号碗的概率是0.5。
    再假定，E表示水果糖，所以问题就变成了在已知E的情况下，来自一号碗的概率有多少？即求P(H1|E)。我们把这个概率叫做”后验概率“，即在事件E发生之后，对P(H1)的修正。
    根据条件概率公式，得到：

• 

朴素贝叶斯分类的原理

---

      朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

朴素贝叶斯分类的正式定义如下：

1、设为一个待分类项，而每个a为x的一个特征属性。

2、有类别集合。

3、计算。

4、如果，则。

根据上述分析，朴素贝叶斯分类的流程可以由下图表示

可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

估计类别下特征属性划分的条件概率及Laplace校准

---

       由上文看出，计算各个划分的条件概率P(a|y)是朴素贝叶斯分类的关键性步骤，当特征属性为离散值时，只要很方便的统计训练样本中各个划分在每个类别中出现的频率即可用来估计P(a|y)，下面重点讨论特征属性是连续值的情况。

当特征属性为连续值时，通常假定其值服从高斯分布（也称正态分布）。即：

而

因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差，代入上述公式即可得到需要的估计值。

另一个需要讨论的问题就是当P(a|y)=0怎么办，当某个类别下某个特征项划分没有出现时，就是产生这种现象，这会令分类器质量大大降低。为了解决这个问题，我们引入Laplace校准，它的思想非常简单，就是对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。