洛谷P3368 【模板】树状数组 2-(区间修改,单点查询)

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 x；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含 N 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 M 行每行包含 2 或 4个整数，表示一个操作，具体如下：

操作 1： 格式：1 x y k 含义：将区间 [x,y] 内每个数加上 k；

操作 2： 格式：2 x 含义：输出第 x 个数的值。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出 #1

6
10

说明/提示

样例 1 解释：

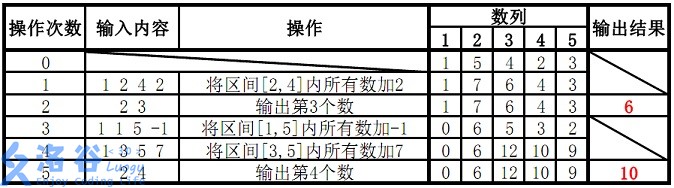
故输出结果为 6、10。

---

数据规模与约定

对于 30% 的数据：N≤8，M≤10；

对于 70% 的数据：N≤10000，M≤10000；

对于 100% 的数据：1≤N,M≤500000，1≤x,y≤n，保证任意时刻序列中任意元素的绝对值都不大于2^30。

代码实现：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
int a[N],b[N],v[N];
int n,m;
int lowbit(int x){
	return x&-x;
}
void update(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i)){
		v[i]+=y;
	}
}
int query(int x){
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))res+=v[i];
	return res;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[i]=a[i]-a[i-1];
		update(i,b[i]);
	}
	for(int i=1;i<=m;i++){
		int k,x,y,z;
		cin>>k;
		if(k==1){
			cin>>x>>y>>z;
			update(x,z);
			update(y+1,-z);
		}else{
			cin>>x;
			cout<<query(x)<<endl;
		}
	}
	return 0;
}