【思维题、KMP】P3526 [POI2011]OKR-Periodicity 题解

P3526 [POI2011]OKR-Periodicity 题解

前言

一道非常厉害的思维题。看题解得到了一些提示搞出来了。

作为 2011 年的题还是很厉害的。

约定

• 定义 \(s[l,r]\) 为 \(s\) 当中下标为 \([l,r]\) 的字符组成的子串。
• \(st,ed\) 表示字符串的某段前缀和后缀。
• 一个串 \(t\) 是 \(s\) 的周期当且仅当 \(s=ttt\dots tt'\)，其中 \(t'\) 是 \(t\) 的前缀。由此知道 \(s[i]=s[i+|t|]\)。
• \(p(p<|s|)\) 是串 \(s\) 的 \(\texttt{border}\) 当且仅当 \(s[1,p]=s[|s|-p+1,|s|]\)。 不难发现 \(|s|-p\) 是 \(s\) 的周期。

题目简述

• 给定由大写字母组成的字符串 \(s\)，构造字典序最小的 \(\texttt{01}\) 串 \(t\) 使得 \(s,t\) 的所有周期长度组成集合相等。（下文称为 \(\texttt{01}\) 表示）
• 多测，\(T\leq 20,|s|\leq 2\times 10^5\)。

解题思路

两个显著的情况：

• 是如果 \(s\) 全部相等，那么肯定构造全 \(\texttt 0\) 串最优。
• 如果 \(s\) 没有周期，那么构造 \(\texttt{000}\dots\texttt{001}\) 肯定最优。

我们先看一个引理：

Weak Periodicity Lemma: 假设 \(s\) 有长度为 \(p,q\) 的周期，且 \(p+q\leq |s|\) 则 \(s\) 有长度为 \(\gcd(p,q)\) 的周期。

证明： 不妨设 \(p<q\)。考虑对于 \(i\leq q-p\)，必然能找到 \(i'\equiv i(\bmod p)\)。必然有 \(i'+q\leq n,i'+q-p> i'\)。由【约定】，我们知道 \(s[i]=s[i']=s[i'+q]=s[i'+q-p]=s[i+q-p]\)，也就是 \(q-p\) 是 \(s\) 的周期。辗转相除可证。

由引理得到推论：

推论：对于 \(s\) 的最小周期 \(r\)，则对于所有的周期 \(R\leq |s|-r\) 只有 \(R\in\{r,2r,\dots, \left\lfloor\dfrac{|s|-r}{r}\right\rfloor\times r\}\)。

转到 \(\texttt{border}\) 上也就是所有 \(\geq r\) 的 \(\texttt{border}\) 只有 \(r+|s|\bmod r,2r+|s|\bmod r+\dots,|s|-r\)。

回到本题当中，分为两种情况：

\(s\) 的最小周期 \(\leq \dfrac{|s|}{2}\)

也就是 \(s\) 可以表示为 \(tt\dots tt'\) 的形式（\(t'\) 是 \(t\) 的前缀）。也可以说 \(s\) 可以表示为 \(t'ttt\dots t\) 的形式（\(t'\) 是 \(t\) 的后缀）。我们先递归求出 \(t't\) 的最小 \(\texttt{01}\) 表示 \(p’p\)。我们下面说明 \(s\) 的最小 \(\texttt{01}\) 表示是 \(p'ppp\dots p\)。首先 \(s\) 的 \(\texttt{border}\) 肯定是 \(t\) 的 \(\texttt{border}\)。所以前 \(|t't|\) 的最小 \(\texttt{01}\) 表示为 \(p'p\)。

观察 \(s\) 的形式如下：

我们已经得到 \(a\) 被 \(t'\) 表示，\(ba\) 被 \(t\) 表示。考虑框起来的一个 \(\texttt{border}\)，可以得到后面的所有 \(ba\) 都会被 \(t\) 表示，证明完毕。合法性显然。

\(s\) 的最小周期 \(>\dfrac{|s|}{2}\)

那么不难发现 \(s\) 可以被表示为 \(tat\) 的形式。其中 \(t\) 是 \(s\) 的最大 \(\texttt{border}\)。我们先求出 \(t\) 的最小表示 \(p\)，下面讨论 \(a\) 可以被替换为 \(\texttt{00}\dots\texttt 0,\texttt{00}\dots\texttt{01}\) 之一。

• 若 \(a\) 被替换为 \(\texttt{00}\dots\texttt 0\)。如果此时不合法，也就是有大于 \(|t|\) 的 \(\texttt{border}\) 出现，我们下面分类讨论。

• • 情况 \(1\)：\(\texttt{border}\) 如下图所示：

这是会发现 \(p\texttt{0}\dots\texttt0=\texttt{0}\dots\texttt0p\)，得到 \(p\) 是全 \(\texttt 0\) 串。

• 情况 \(2\)：\(\texttt{border}\) 对应情况如下图所示：

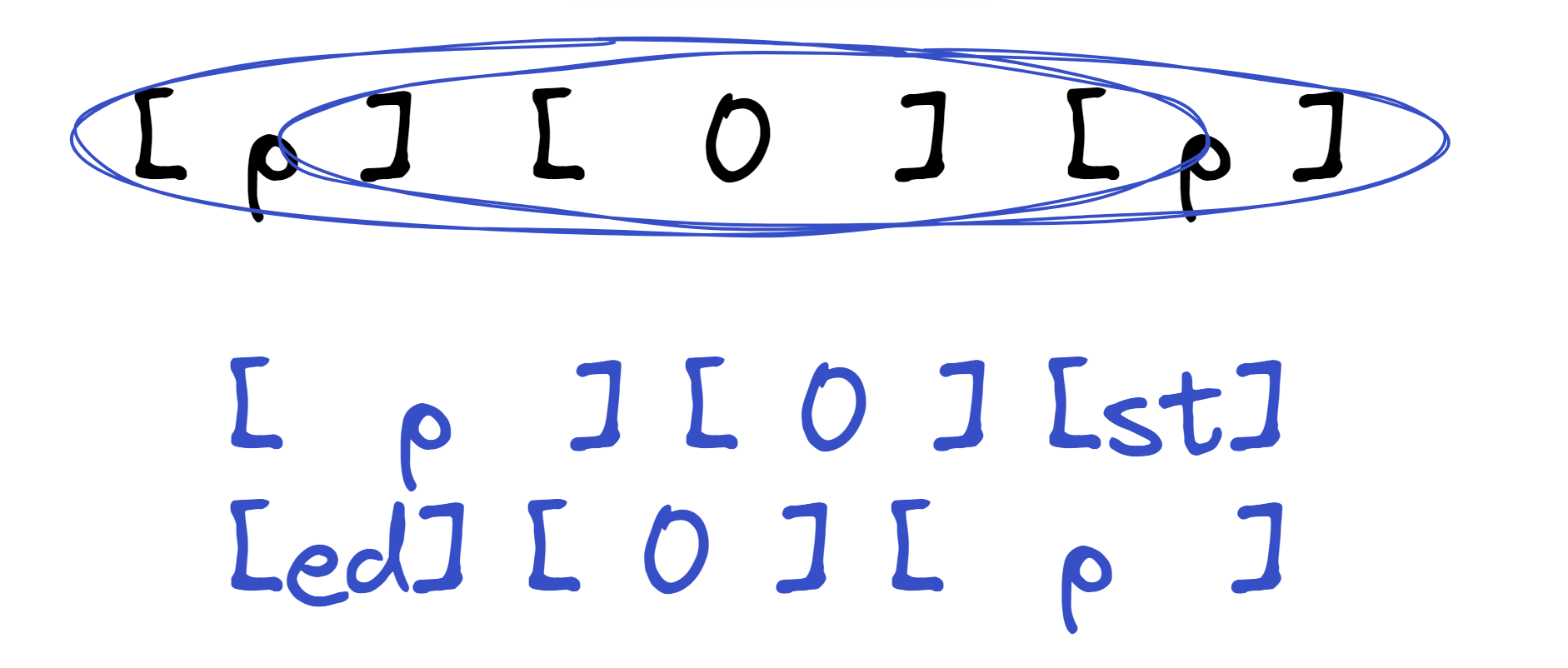
这个时候也不难得出 \(p\) 是全 \(\texttt0\) 串。

• 情况 \(3\)：\(\texttt{border}\) 对应关系如下图所示：

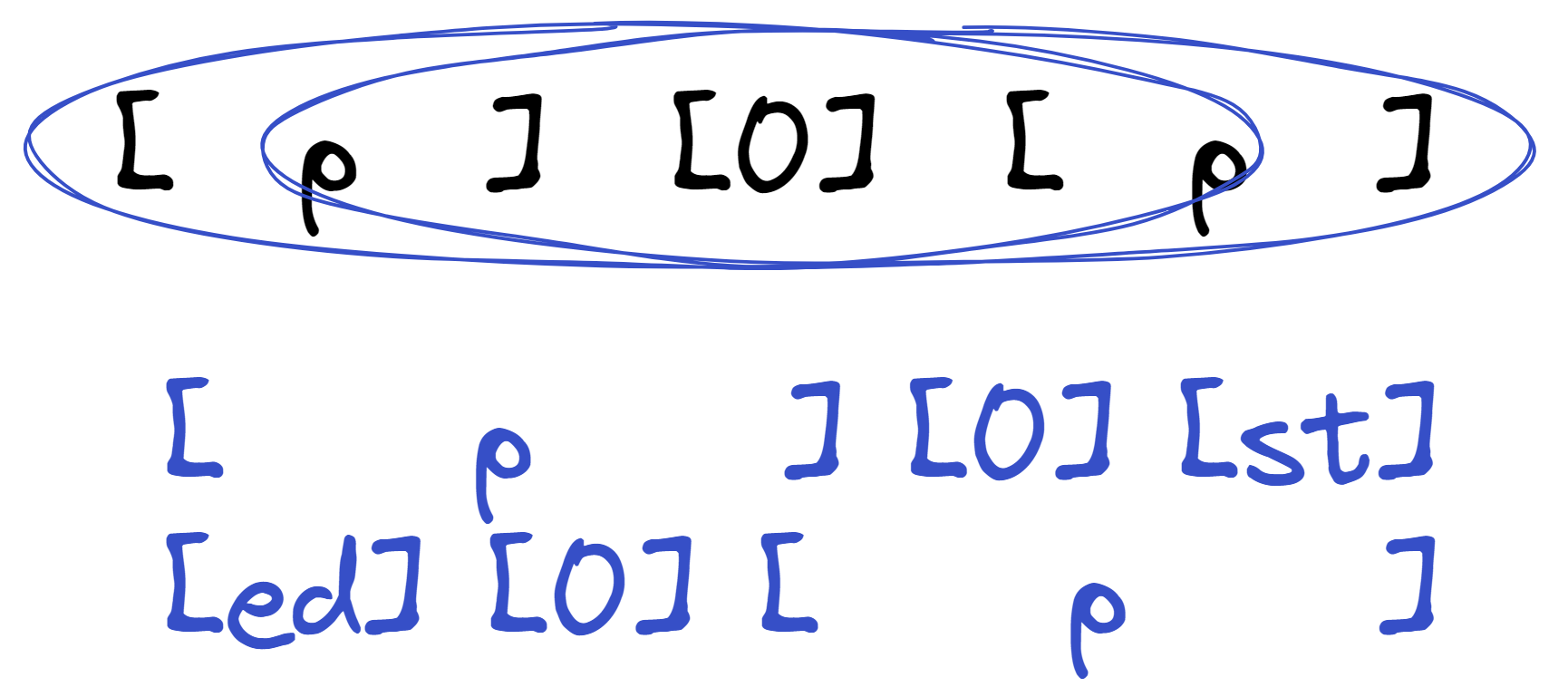
我们什么也得不到。但是不难得到全 \(\texttt 0\) 串也满足情况 \(3\)，所以只有情况 \(3\) 不满足。当时当我们把 \(a\) 表示换为 \(\texttt 0\dots\texttt {01}\) 的时候，\(a\) 在 \(\texttt{border}\) 当中的位置肯定和上面的位置一样，这时候就不满足了。证毕。

至此我们讨论完了所有 \(s\) 的情况，可以递归解决。

具体实现

我们梳理一下我们的递归函数 dfs(p) 需要干什么。

他的目的应当是寻找 \(s[1,p]\) 的最小表示。上面讨论了 \(4\) 种情况：

• \(s[1,p]\) 全部字符相等。把答案对应位全填 \(\texttt 0\)。
• \(s[1,p]\) 没有 \(\texttt{border}\)。除了最后一位填 \(\texttt 1\) 其他填 \(\texttt 0\)。
• \(s[1,p]\) 最小周期 \(len\) 满足 \(2len\leq p\)，递归求出 \(p\bmod len+len\) 的表示，重复到后面得到答案。
• 否则最大 \(\texttt{border}\) 为 \(len\)，递归求 \(len\) 的表示。尝试把答案 \(len+1,p-len\) 填入全 \(\texttt 0\) 查询是否合法，不合法把最后一位改为 \(\texttt 1\)。

给一份 dfs 及其他函数的参考代码：

const int MAXN=2e5+5;
char s[MAXN];int border[MAXN],fail[MAXN];
char ans[MAXN];
void KMP(int n,char *t,int *p){
	p[1]=0;
	for(int i=2;i<=n;i++){
		p[i]=p[i-1];
		while(p[i]&&t[p[i]+1]!=t[i]) p[i]=p[p[i]];
		if(t[p[i]+1]==t[i]) p[i]++;
	}
}
void dfs(int p){
	bool sm=1;
	for(int i=1;i<=p;i++) if(s[i]!=s[1]) sm=0;
	if(sm){for(int i=1;i<=p;i++) ans[i]='0';return;}
	if(border[p]==0){for(int i=1;i<=p-1;i++) ans[i]='0';ans[p]='1';return;}
	int len=p-border[p];// 周期长度
	if(len*2<=p){
		dfs(len+p%len);
		for(int i=len+p%len+1;i<=p;i++)
			ans[i]=ans[i-len];
		return;
	}
	len=border[p];
	dfs(len);
	for(int i=len+1;i<=p-len;i++) ans[i]='0';
	for(int i=1;i<=len;i++)
		ans[p-len+i]=ans[i];
	KMP(p,ans,fail);
	if(fail[p]!=len) ans[p-len]='1';
	return;
}
void solve(){
	cin>>(s+1);int n=strlen(s+1);
	KMP(n,s,border);
	dfs(n);
	for(int i=1;i<=n;i++) putchar(ans[i]);
	puts("");
}