Gene Ontology（GO）是基因功能国际标准分类体系。GO富集分析是对差异基因等按GO分类，并对分类结果进行基于离散分布的显著性分析、错判率分析、富集度分析，得到与实验目的有显著联系的、低误判率的、靶向性的基因功能分类，该分类即导致样本性状差异的最重要的功能差别。在芯片的数据分析中，研究者可以找出哪些变化基因属于一个共同的GO功能分支，并用统计学方法检定结果是否具有统计学意义，从而得出变化基因主要参与了哪些生物功能。

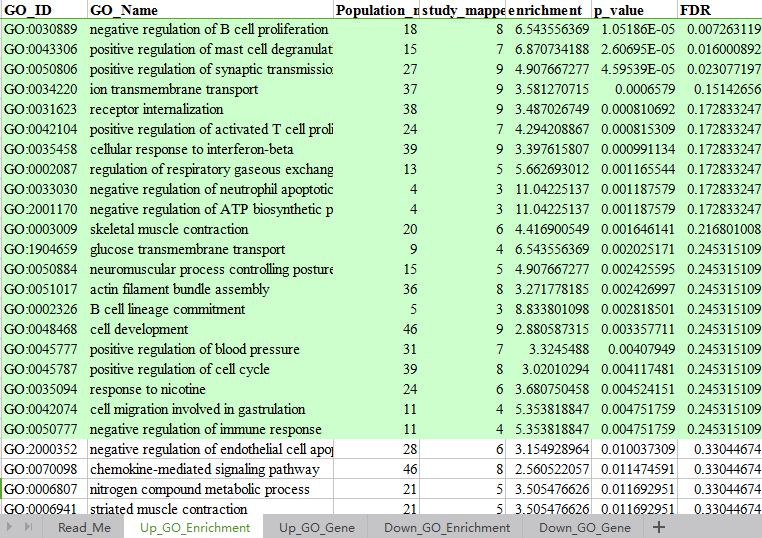
1.      对mRNA进行显著性功能富集分析，得到具有显著性、靶向性的功能以及显著性功能对应的靶基因。（功能富集）
 

2.      对富集得到的显著性功能以柱状图的形式展示。（功能柱状图）
 

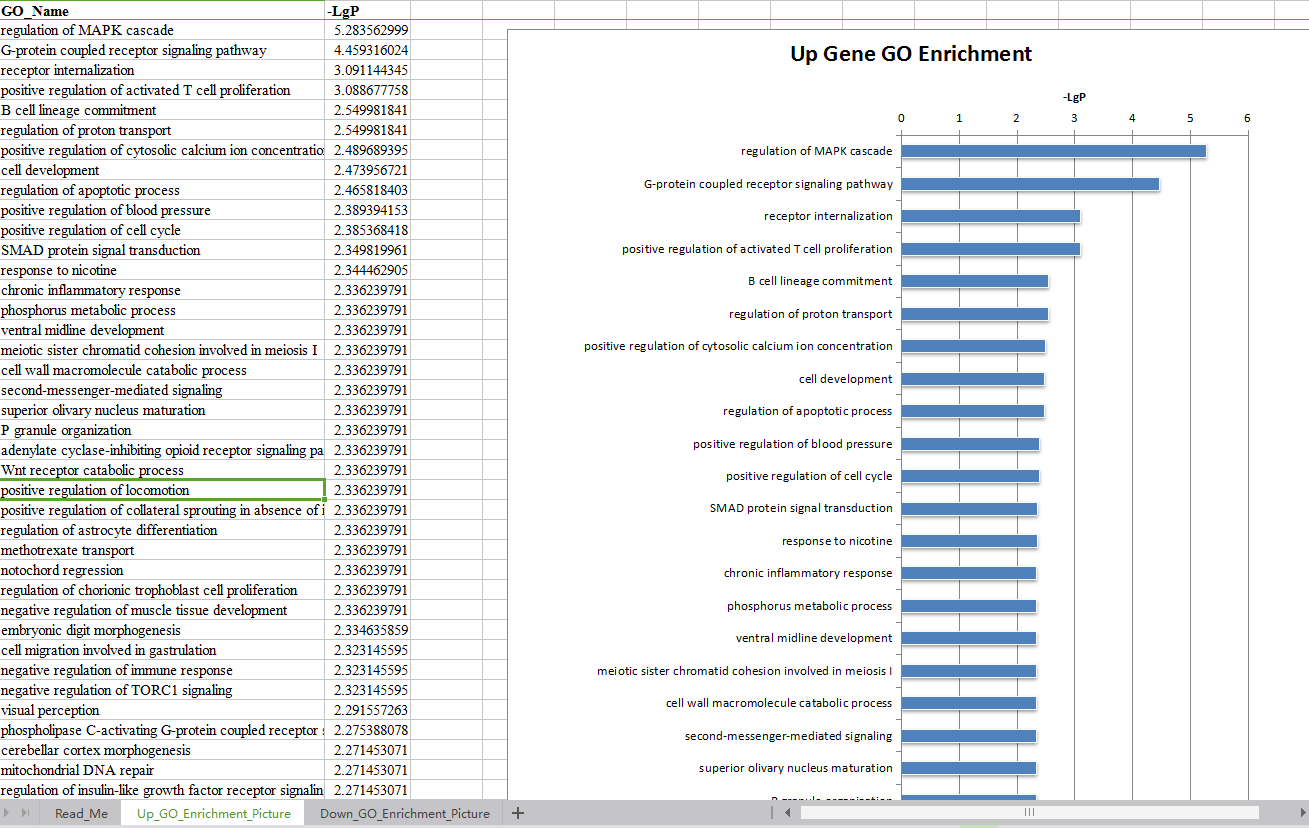
3.      对富集得到的显著性功能以点图的形式展示。（功能点图）

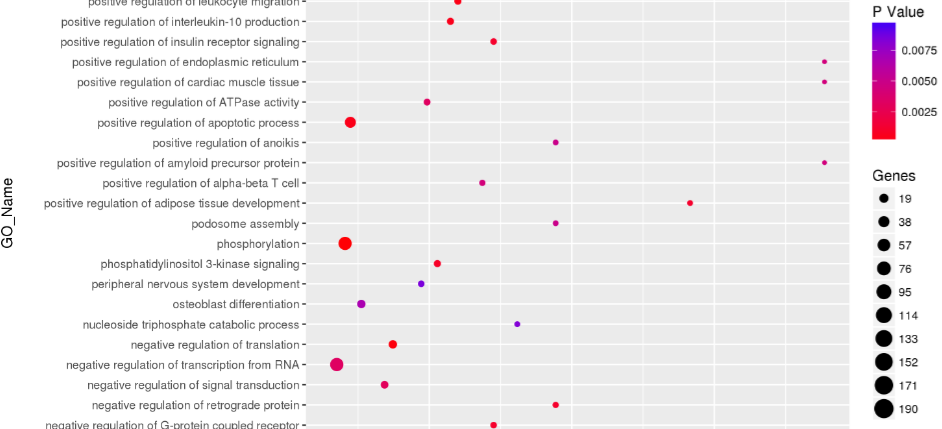
功能的显著性分析——GO Enrichment Analysis的更多相关文章

  1. GSEA - Gene set enrichment analysis 基因集富集 | ORA - Over-Representation Analysis 分析原理与应用

    RNA-seq是利器,大部分做实验的老板手下都有大量转录组数据,所以RNA-seq的分析需求应该是很大的(大部分的生信从业人员应该都差不多要沾边吧). 普通的转录组套路并不多,差异表达基因.富集分析. ...

  2. [protocol]GO enrichment analysis

    [protocol]GO enrichment analysis     背景: 什么是富集分析,自己可以百度.我到目前也没发现一个比较通俗易懂的介绍.直接理解为一种统计学方法就可以了. 用于查看显著 ...

  3. BABOK － 企业分析（Enterprise Analysis）

    BABOK - 企业分析(Enterprise Analysis)概要 发表于2013年10月9日由周金根 描述 企业分析描述我们如何捕捉.提炼并明晰业务需要,并定义一个可能实现这些业务需要的一个方案 ...

  4. 帕累托分析法(Pareto Analysis)(柏拉图分析)

    帕累托分析法(Pareto Analysis)(柏拉图分析) ABC分类法是由意大利经济学家帕雷托首创的.1879年,帕累托研究个人收入的分布状态图是地,发现少数人收入占全部人口收入的大部分,而多数人 ...

  5. 【Cocos游戏实战】功夫小子第七课之游戏主功能场景逻辑功能和暂停功能场景的分析和实现

    CSDN的markdown编辑器是吃屎了么! !.什么玩意.!写了一半写不了东西还全没了,搞个毛线! 本节课的视频教程地址是:第七课在此 假设本教程有帮助到您,希望您能点击进去观看一下,并且如今注冊成 ...

  6. Java安全（权限）框架 - Shiro 功能讲解 架构分析

    Java安全(权限)框架 - Shiro 功能讲解 架构分析 作者 : Stanley 罗昊 [转载请注明出处和署名,谢谢!] 简述Shiro Shiro出自公司Apache(阿帕奇),是java的一 ...

  7. GWAS条件分析（conditional analysis）

    一.为什么要做GWAS的条件分析(conditional analysis) 我们做GWAS的时候,经常扫出一堆显著的信号,假设rs121是我们扫出来与某表型最显著相关的位点(P=1.351e-36) ...

  8. 论坛：设计实体-->分析功能-->实现功能 之 《分析功能》

    其中 管理文章 的功能没有做,以下做的设计 浏览与参与 功能的步骤 分析功能   5个功能.   7个请求. 实现功能   Action, 7个方法   Service   Dao   Jsp For ...

  9. BMDP为常规的统计分析提供了大量的完备的函数系统，如：方差分析（ANOVA）、回归分析（Regression）、非参数分析（Nonparametric Analysis）、时间序列（Times Series）等等。此外，BMDP特别擅于进行出色的生存分析（Survival Analysis ）。许多年来，一大批世界范围内顶级的统计学家都曾今参与过BMDP的开发工作。这不仅使得BMDP的权威性得到

        BMDP是Bio Medical Data Processing的缩写,是世界级的统计工具软件,至今已经有40多年的历史.目前在国际上与SAS.SPSS被并称为三大统计软件包.BMDP是一个大 ...

随机推荐

  1. UOJ244 短路 贪心

    正解:贪心 解题报告: 传送门! 贪心真的都是些神仙题,,,以我的脑子可能是不存在自己想出解这种事情了QAQ 然后直接港这道题解法趴,,, 首先因为这个是对称的,所以显然的是可以画一条斜右上的对角线, ...

  2. django时间的时区问题（转）

    add by zhj: 使用django时,如果设置USE_TZ=True,那django在数据库中存储的是0时区的时间:如果USE_TZ=False,那存储的是本地时间 原文:https://www ...

  3. [GDOI2018]滑稽子图

    题目链接:[被和谐] 题目大意:对于一棵树$(V,E)$,对于$S\subset V$,$f(S)$为点集$S$的导出子图的边数.求$\sum_{S\subset V}f(S)^k$ 这里的导出子图说 ...

  4. JavaScript indexOf() 方法

    定义和用法 indexOf() 方法可返回某个指定的字符串值在字符串中首次出现的位置. 语法 stringObject.indexOf(searchvalue,fromindex) 说明 该方法将从头 ...

  5. 【托业】【新托业TOEIC新题型真题】学习笔记3-题库二->P5-6

    --------------------------------------单词-------------------------------------- oppose vt. 反对:对抗,抗争 v ...

  6. MySQL大表DROP删除小技巧(转)

    在日常工作中,经常会遇到历史大表从主库上迁移到备份机,以便腾出主库空间,那么如果你直接drop table 后,可能会引起数据库抖动,连接数升高等问题,从而影响业务. 那么用一个小技巧,即可轻松平滑的 ...

  7. UltraISO 9.7.0.3476中文完美破解安装版

    https://cn.ultraiso.net/uiso9_cn.exe 简体中文版专用:        注册名:Guanjiu 注册码:A06C-83A7-701D-6CFC 多国语言版专用: 注册 ...

  8. 技嘉主板BIOS恢复方法

    技嘉的dual bios技术的原理很简单,在main bios能启动的情况下,backup bios不会对bios进行检测.只有当main bios出现故障(这个故障一般是软件故障)才会从backup ...

  9. vue中让input框自动聚焦

    created(){ this.changfouce(); }, methods: { //在vue生命周期的created()钩子函数进行的DOM操作要放在Vue.nextTick()的回调函数中, ...

  10. C 逗號表達式 與返回值

    逗號表達式的返回值是最後一個表達式的值 int z; z=(,); printf("%d\n",z);//6 int a; printf(*,a*,a+));//20 a=3*5, ...