SSH加密原理、RSA非对称加密算法学习与理解

首先声明一下，这里所说的SSH，并不是Java传统的三大框架，而是一种建立在应用层和传输层基础上的安全外壳协议，熟悉Linux的朋友经常使 用到一 个SSH Secure Shell Cilent的工具，本文也是基于此工具加密原理的学习，在SSH的加密原理中，使用到了RSA非对称加密算法，本文也一并做了学习和了解。

非对称加密算法

在日常的工作生产中， 我们经常需要进行数据的通讯，开发人员经常需要对数据进行加解密操作，以保证数据的安全。数据的加密算法非为对称加密和非对称加密两种，常用的DES、三 重DES、AES等都属于对称加密，即通过一个密钥可以进行数据的加解密，密钥一旦泄漏，传输的数据则不安全。

非对称加密算法的核心源于数学问题，它存在公钥和私钥的概念，要完成加解密操作，需要两个密钥同时参与。我们常说的“公钥加密，私钥加密”或“私钥加密， 公钥解密”都属于非对称加密的范畴，后文中讲到的RSA算法也一种典型的非对称加密算法。公钥加密的数据必须使用私钥才可以解密，同样，私钥加密的数据也 只能通过公钥进行解密。

相比对称加密，非对称加密的安全性得到了提升，但是也存在明显的缺点，非对称加解密的效率要远远小于对称加解密。所以非对称加密往往被用在一些安全性要求比较高的应用或领域中。

    典型的RSA非对称加密

RSA加密算法是一种典型的非对称加密算法，它基于大数的因式分解数学难题，它也是应用最广泛的非对称加密算法，于1978年由美国麻省理工学院（MIT）的三位学着：Ron Rivest、Adi Shamir 和 Leonard Adleman 共同提出。

它的原理较为简单，我们假设有消息发送方A和消息接收方B，通过下面的几个步骤，我们就可以完成消息的加密传递：

1. 消息发送方A在本地构建密钥对，公钥和私钥；

2. 消息发送方A将产生的公钥发送给消息接收方B；

3. B向A发送数据时，通过公钥进行加密，A接收到数据后通过私钥进行解密，完成一次通信；

4. 反之，A向B发送数据时，通过私钥对数据进行加密，B接收到数据后通过公钥进行解密。

由于公钥是消息发送方A暴露给消息接收方B的，所以这种方式也存在一定的安全隐患，如果公钥在数据传输过程中泄漏，则A通过私钥加密的数据就可能被解密。

如果要建立更安全的加密消息传递模型，需要消息发送方和消息接收方各构建一套密钥对，并分别将各自的公钥暴露给对方，在进行消息传递时，A通过B的公钥对数据加密，B接收到消息通过B的私钥进行解密，反之，B通过A的公钥进行加密，A接收到消息后通过A的私钥进行解密。

当然，这种方式可能存在数据传递被模拟的隐患，我们可以通过数字签名等技术进行安全性的进一步提升。由于存在多次的非对称加解密，这种方式带来的效率问题也更加严重。

    SSH加密原理

在SSH安全协议的原理中， 是一种非对称加密与对称加密算法的结合，先看下图：

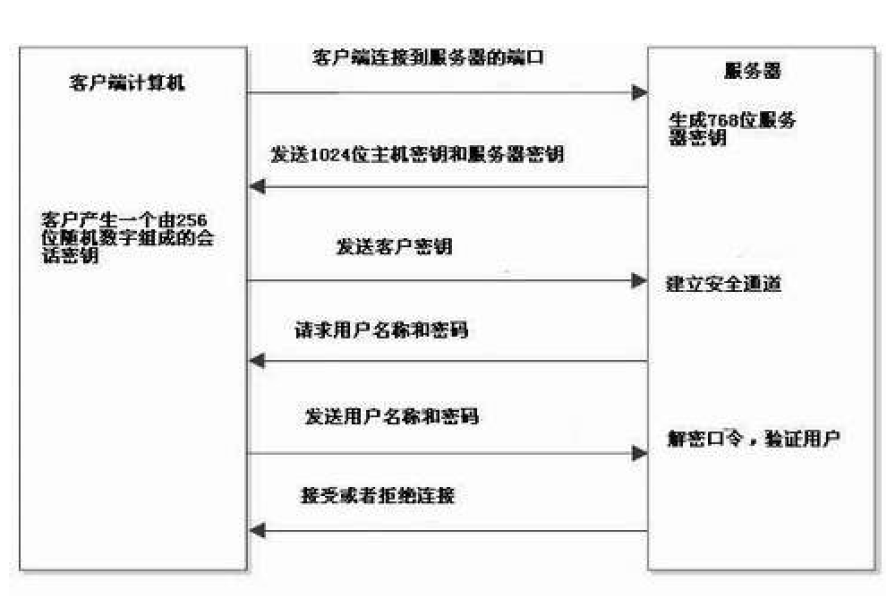
这里进行一下说明：

1. 首先服务端会通过非对称加密，产生一个公钥和私钥；

2. 在客户端发起请求时，服务端将公钥暴露给客户端，这个公钥可以被任意暴露；

3. 客户端在获取公钥后，会先产生一个由256位随机数字组成的会话密钥，这里称为口令；

4. 客户端通过公钥将这个口令加密，发送给服务器端；

5. 服务器端通过私钥进行解密，获取到通讯口令；

6. 之后，客户端和服务端的信息传递，都通过这个口令进行对称的加密。

个人感觉，这样的设计在一定程度上提高了加解密的效率，不过，与客户端服务端各构建一套密钥对的加解密方式相比，在安全性上可能有所下降。在上面所述的通过口令进行加密的过程中，数据也是可以被窃听的，不过由于密钥是256个随机数字，有10的256次方中组合方式，所以破解难度也很大。相对还是比较安全的。服务端和客户端都提前知道了密钥，SSH的这种方式，服务端是通过解密获取到了密钥。

DH密钥交换算法

SSH的原理，是基于RSA非对称加密，RSA是基于大数的因式分解数学难题，下面要提到的DH密钥交换算法则是基于有限域上的离散对数难题。

DH算法是一种密钥协商算法，只用于密钥的分配，不用于消息的加解密。它提供了一种安全的交换密钥的方式，通过交换的密钥进行数据的加解密。就像SSH原理中，口令的交换，不过DH算法更安全。

我们举个例子来进行说明，假设有A、B两方，A作为发送者，B作为接收者。通过下面的几个步骤就可以构建出一个只属于双方的密钥口令，如下：

1. 首先A、B双方，在通信前构建专属于自己的密钥对，假设分别是公钥A，私钥A，公钥B，私钥B；

2. A将自己的公钥A暴露给B，B通过私钥B和公钥A经过一定的运算产生出本地的密钥B；

3. 同样，B将自己的公钥B暴露给A，A通过私钥A和公钥B经过一定的运算产生出本地的密钥A；

4. 最后，这个算法有意思的一点就是，密钥A和密钥B是一致的，这样A、B双方就拥有了一个属于双方的“秘密”口令；

DH算法的产生是，对称加密向非对称加密的过度，为后续非对称加密的产生和发展奠定了基础。