orocos_kdl学习（一）：坐标系变换

　　KDL中提供了点(point)、坐标系(frame)、刚体速度(twist)，以及6维力/力矩(wrench)等基本几何元素，具体可以参考 Geometric primitives 文档。

Creating a Frame, Vector and Rotation

　　PyKDL中创建一个坐标系时有下面4种构造函数：

__init__()         # Construct an identity frame

__init__(rot, pos) # Construct a frame from a rotation and a vector
# Parameters:
# pos (Vector) – the position of the frame origin
# rot (Rotation) – the rotation of the frame

__init__(pos)      # Construct a frame from a vector, with identity rotation
# Parameters:
# pos (Vector) – the position of the frame origin

__init__(rot)      # Construct a frame from a rotation, with origin at 0, 0, 0
# Parameters:
# rot (Rotation) – the rotation of the frame

　　下面是一个例子：

#! /usr/bin/env python

import PyKDL

# create a vector which describes both a 3D vector and a 3D point in space
v = PyKDL.Vector(1,3,5)

# create a rotation from Roll Pitch, Yaw angles
r1 = PyKDL.Rotation.RPY(1.2, 3.4, 0)

# create a rotation from ZYX Euler angles
r2 = PyKDL.Rotation.EulerZYX(0, 1, 0)

# create a rotation from a rotation matrix
r3 = PyKDL.Rotation(1,0,0, 0,1,0, 0,0,1)

# create a frame from a vector and a rotation
f = PyKDL.Frame(r2, v)

print f

　　结果将如下所示，前9个元素为代表坐标系姿态的旋转矩阵，后三个元素为坐标系f的原点在参考坐标系中的坐标。

[[    0.540302,           0,    0.841471;
            0,           1,           0;
    -0.841471,           0,    0.540302]
[           1,           3,           5]]

　　根据机器人学导论（Introduction to Robotics Mechanics and Control）附录中的12种欧拉角表示方法，ZYX欧拉角代表的旋转矩阵为：

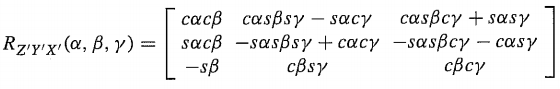
　　代入数据验证，KDL的计算与理论一致。

Extracting information from a Frame, Vector and Rotation

　　PyKDL中坐标系类Frame的成员M为其旋转矩阵，p为其原点坐标。

#! /usr/bin/env python

import PyKDL

# frame
f = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0),
                PyKDL.Vector(3,2,4))

# get the origin (a Vector) of the frame
origin = f.p

# get the x component of the origin
x = origin.x()
x = origin[0]
print x

# get the rotation of the frame
rot = f.M
print rot

# get ZYX Euler angles from the rotation
[Rz, Ry, Rx] = rot.GetEulerZYX()
print Rz,Ry,Rx

# get the RPY (fixed axis) from the rotation
[R, P, Y] = rot.GetRPY()
print R,P,Y

　　将上述获取到的数据打印出来，结果如下：

3.0
[    0.540302,           0,    0.841471;
            0,           1,           0;
    -0.841471,           0,    0.540302]
0.0 1.0 0.0
0.0 1.0 0.0

　　注意GetEulerZYX和GetRPY的结果是一样的，这其实不是巧合。因为坐标系的旋转有24种方式（本质上只有12种结果）：绕自身坐标系旋转有12种方式（欧拉角），绕固定参考坐标系旋转也有12种方式（RPY就是其中一种）。EulerZYX按照Z→Y→X的顺序绕自身坐标轴分别旋转$\alpha$、$\beta$、$\gamma$角；RPY按照X→Y→Z的顺序绕固定坐标系旋转$\gamma$、$\beta$、$\alpha$角，这两种方式最后得到的旋转矩阵是一样的。

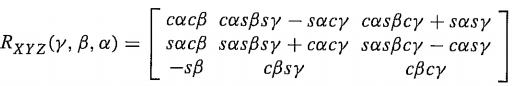
Transforming a point

　　frame既可以用来描述一个坐标系的位置和姿态，也可以用于变换。下面创建了一个frame，然后用其对一个空间向量或点进行坐标变换：

#! /usr/bin/env python

import PyKDL

# define a frame
f = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0),
                PyKDL.Vector(3,2,4))

# define a point
p = PyKDL.Vector(1, 0, 0)
print p

# transform this point with f
p = f * p
print p

Creating from ROS types

　　tf_conversions这个package包含了一系列转换函数，用于将tf类型的数据(point, vector, pose, etc) 转换为与其它库同类型的数据，比如KDL和Eigen。用下面的命令在catkin_ws/src中创建一个测试包：

catkin_create_pkg test rospy tf geometry_msgs

　　test.py程序如下（注意修改权限chmod +x test.py）：

#! /usr/bin/env python
import rospy
import PyKDL
from tf_conversions import posemath
from geometry_msgs.msg import Pose

# you have a Pose message
pose = Pose()

pose.position.x = 1
pose.position.y = 1
pose.position.z = 1
pose.orientation.x = pose.orientation.y = pose.orientation.z = 0
pose.orientation.w = 1

# convert the pose into a kdl frame
f1 = posemath.fromMsg(pose)

# create another kdl frame
f2 = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0),
                 PyKDL.Vector(3,2,4))

# Combine the two frames
f = f1 * f2
print f

[x, y, z, w] = f.M.GetQuaternion()
print x,y,z,w

# and convert the result back to a pose message
pose = posemath.toMsg(f)

pub = rospy.Publisher('pose', Pose, queue_size=1)
rospy.init_node('test', anonymous=True)
rate = rospy.Rate(1) # 1hz

while not rospy.is_shutdown():
    pub.publish(pose)
    rate.sleep()

　　通过posemath.toMsg可以将KDL中的frame转换为geometry_msgs/Pose类型的消息。最后为了验证，创建了一个Publisher将这个消息发布到pose话题上。使用catkin_make编译后运行结果如下：

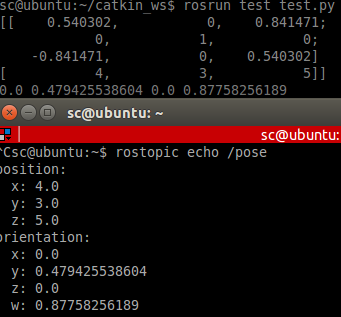
参考：

KDL Geometric primitives

从URDF到KDL(C++&Python)

PyKDL 1.0.99 documentation

Orocos Kinematics and Dynamics

kdl / Tutorials / Frame transformations (Python)