[NOIP2009]最优贸易（图论）

[NOIP2009]最优贸易

题目描述

CC 国有 \(n\) 个大城市和 \(m\) 条道路，每条道路连接这 \(n\) 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 \(m\) 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 \(1\) 条。

CC 国幅员辽阔，各地水晶球价格 ≤100的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 CC 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 CC 国 \(n\) 个城市的标号从 \(1~ n\) ，阿龙决定从 \(1\) 号城市出发，并最终在 \(n\) 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 \(n\) 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 CC 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 CC 国有 \(5\) 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

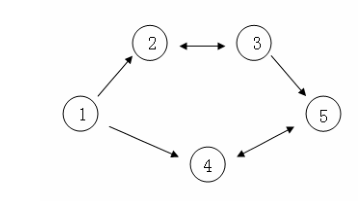
假设 \(1~n\) 号城市的水晶球价格分别为 4,3,5,6,14,3,5,6,1 。

阿龙可以选择如下一条线路： \(1\) -> \(2\) -> \(3\) -> \(5\) ，并在 \(2\) 号城市以 \(3\) 的价格买入水晶球，在 \(3\) 号城市以 \(5\) 的价格卖出水晶球，赚取的旅费数为 \(2\)。

阿龙也可以选择如下一条线路 \(1\) -> \(4\) -> \(5\) -> \(4\) -> \(5\) ，并在第 \(1\) 次到达 \(5\) 号城市时以 \(1\) 的价格买入水晶球，在第 \(2\) 次到达 \(4\) 号城市时以 \(6\) 的价格卖出水晶球，赚取的旅费数为 \(5\) 。

现在给出 \(n\) 个城市的水晶球价格， \(m\) 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 \(2\) 个正整数 \(n\) 和 \(m\) ，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 \(n\) 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 \(n\) 个城市的商品价格。

接下来 \(m\) 行，每行有 \(3\) 个正整数 \(x,y,z\) ，每两个整数之间用一个空格隔开。如果 \(z=1\) ，表示这条道路是城市 \(x\) 到城市 \(y\) 之间的单向道路；如果 \(z=2\) ，表示这条道路为城市 \(x\) 和城市 \(y\) 之间的双向道路。

输出格式：

一 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 \(0\) 。

输入输出样例

输入样例#1：

5 5

4 3 5 6 1

1 2 1

1 4 1

2 3 2

3 5 1

4 5 2

输出样例#1：

5

说明

【数据范围】

输入数据保证 \(1\) 号城市可以到达 \(n\) 号城市。

对于 10%的数据， \(1≤n≤6\)。

对于 30%的数据， \(1≤n≤100\) 。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据， \(1≤n≤100000\) ， \(1≤m≤500000\) ， \(1≤x\) ， \(y≤n\) ， \(1≤z≤2\) ， \(1≤\) 各城市

水晶球价格 \(≤100\) 。

对于图论一无所知，想了很久没想到怎么做。

最开始想到用差分的思想，每条边存下\(a[to]-a[from]\)，然后\(dis[i]\)变成了表示在\(1\)买，\(i\)卖出的钱数。跑完最短路之后，要用\(n^2\)来枚举任意两点做起点终点的情况判断\(ans\)。

看了题解之后考虑到我们只需要考虑在哪个点买，在哪个点卖即可求出\(ans\)最优，运用dp的思想，求出每个点前面（\(1-x\)的路径）的最小值和后面（\(x-n\)的路径）的最大值。建一个正向图和一个反向图，分别以\(1\)和\(n\)作为起点更新每个点的最小最大值。枚举每个节点判断即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int read()
{
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*w;
}
const int N=100010;
int n,m,cnt;
int head[N],x[5*N],y[5*N],z[5*N],dis1[N],dis2[N],vis[N],a[N];
struct node{
    int to,next;
}edge[10*N];
queue <int> q;
void add(int x,int y)
{
    cnt++;
    edge[cnt].to=y;
    edge[cnt].next=head[x];
    head[x]=cnt;
}
void work1()
{
    memset(dis1,0x3f,sizeof(dis1));
    while(q.size()) q.pop();
    q.push(1);dis1[1]=a[1];
    while(!q.empty())
    {
        int u=q.front();q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            dis1[v]=min(dis1[u],a[v]);
            q.push(v);
        }
    }
}
void init()
{
    cnt=0;memset(head,0,sizeof(head));memset(vis,0,sizeof(vis));
    for(int i=1;i<=m;i++)
    {
        add(y[i],x[i]);
        if(z[i]==2) add(x[i],y[i]);
    }
}
void work2()
{
    memset(dis2,-1,sizeof(dis2));
    while(q.size()) q.pop();
    q.push(n);dis2[n]=a[n];
    while(!q.empty())
    {
        int u=q.front();q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            dis2[v]=max(dis2[u],a[v]);
            q.push(v);
        }
    }
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    for(int i=1;i<=m;i++)
    {
        x[i]=read();y[i]=read();z[i]=read();
        add(x[i],y[i]);
        if(z[i]==2) add(y[i],x[i]);
    }
    work1();
    init();
    work2();
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        ans=max(ans,dis2[i]-dis1[i]);
    }
    cout<<ans;
}