AcWing 225. 矩阵幂求和 （矩阵快速幂+分治）打卡

题目：https://www.acwing.com/problem/content/227/

题意：给你n，k,m，然后输入一个n阶矩阵A，让你求  S=A+A^2+A^3.+......+A^k

思路：首先因为A是矩阵，我们k的范围很大，那么很明显看出A^k可以用矩阵快速幂来计算，但是这样我们只能算出其中一项，还是有k项，那么我们怎么计算和呢

我们可以看出前一项和后一项是有关联的，就是乘了一个A，我们怎么利用前面计算的结果呢，On遍历肯定不行，既然我们用到了遍历，那么优化我们很容易想到二分

假设我们    A+A^2+A^3+A^4+A^5+A^6

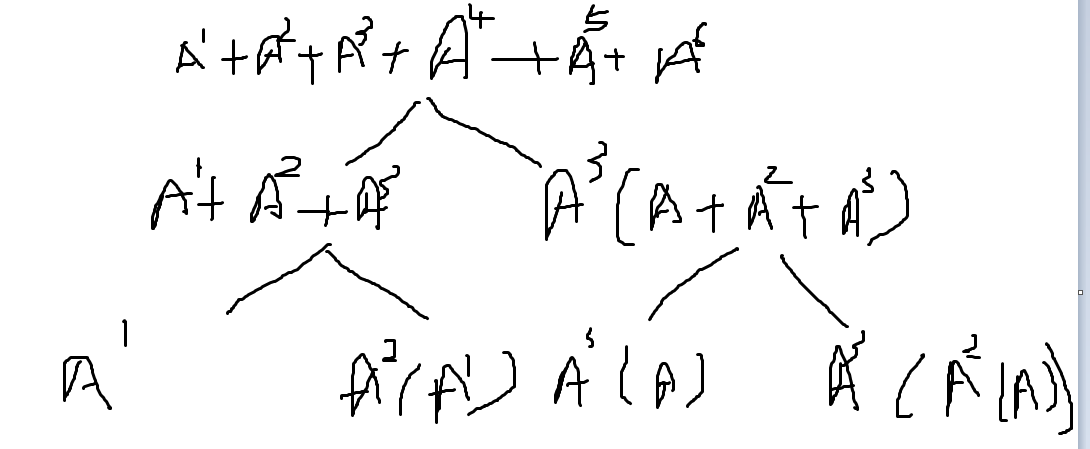
那么可以利用类似分治的方法，一直这样二分递归下去，然后我们自底向上，以左子树推出又子树，这样就能得到最终的答案

#include<bits/stdc++.h>
using namespace std;
#define MAXN 35
typedef long long ll;
int n,mod;
struct mat
{
    ll m[MAXN][MAXN];//矩阵结构体
}unit;//unit为单位矩阵，即主对角线全部为1，这样任何矩阵与单位矩阵相乘都为它本身

mat msub(mat a,mat b)//矩阵相乘函数
{
    mat ret;
    ll x;
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
        {
            x=;
            for(int k=;k<n;k++)
            {
                x+=((a.m[i][k]*b.m[k][j])%mod);//取余
            }
            ret.m[i][j]=x%mod;//取余
        }
    }
    return ret;
}
mat add(mat a,mat b)//矩阵相乘函数
{
    mat ret;
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
        {
            ret.m[i][j]=(a.m[i][j]+b.m[i][j])%mod;
        }
    }
    return ret;
}

void init_unit()//初始化单位矩阵
{
    for(int i=;i<MAXN;i++)
    {
        unit.m[i][i]=;
    }
}

mat qpow(mat a,ll x)//快速幂
{
    mat ans=unit;
    while(x)
    {
        if(x&) ans=msub(ans,a);
        a=msub(a,a);
        x>>=;
    }
    return ans;
}

mat sum(mat a,ll k){
    if(k==) return a;
    mat w=sum(a,k/);
    if(k%){
        mat ans=qpow(a,k/+);
        ans=add(ans,msub(ans,w));
        return add(w,ans);
    }
    else{
        mat ans=qpow(a,k/);
        return add(w,msub(ans,w));
    }
}
int main()
{
    ll x;
    init_unit();
    cin>>n>>x>>mod;
    mat a,ans;
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
        {
            cin>>a.m[i][j];
        }
    }
    ans=sum(a,x);
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
        {
            if(j!=n-) cout<<ans.m[i][j]<<" ";
            else cout<<ans.m[i][j]<<endl;
        }
    }
    return ;
}