「BalticOI 2011」Switch the Lamp On

Casper is designing an electronic circuit on a \(N \times M\) rectangular grid plate. There are \(N \times M\) square tiles that are aligned to the grid on the plate. Two (out of four) opposite corners of each tile are connected by a wire.

A power source is connected to the top left corner of the plate. A lamp is connected to the bottom right corner of the plate. The lamp is on only if there is a path of wires connecting power source to lamp. In order to switch the lamp on, any number of tiles can be turned by 90° (in both directions).

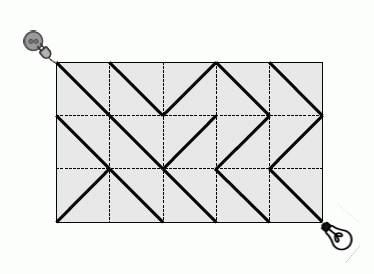
In the picture above the lamp is off. If any one of the tiles in the second column from the right is turned by 90° , power source and lamp get connected, and the lamp is on.

Write a program to find out the minimal number of tiles that have to be turned by 90° to switch the lamp on.

有一种正方形的电路元件，在它的两组相对顶点中，有一组会用导线连接起来，另一组则不会。

有 \(N\times M\) 个这样的元件，你想将其排列成 \(N\) 行 \(M\) 列放在电路板上。电路板的左上角连接电源，右下角连接灯泡。

试求：至少要旋转多少个正方形元件才能让电源与灯泡连通。 \(1 \le N,M \le 500\)。

原电路连边权为 0 的边，反向对角线连边权为 1 的边，求最短路。

暴力解法：Dijkstra 堆优化，堆要用手写堆或 STL 手动堆。

正解：边权仅为 0 或 1 的图，显然用 deque 广搜，边权为 0 的 push_front，边权为 1 的 push_back。

以下是 暴力解法。正解不会写……

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;

int n, m, d[260005];
char str[505]; bool v[260005];
int head[260005], nex[260005<<2], to[260005<<2], w[260005<<2];
struct node {
	int t, d;
	bool operator < (const node& A) const {return d>A.d; }
};
node q[260005<<2]; int qt;

inline int id(const int& x, const int& y) {
	return (x-1)*(m+1)+y;
}
inline void add(const int& x, const int& y, const int& z) {
	nex[++head[0]]=head[x], head[x]=head[0], to[head[0]]=y, w[head[0]]=z;
	nex[++head[0]]=head[y], head[y]=head[0], to[head[0]]=x, w[head[0]]=z;
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i=1; i<=n; ++i) {
		scanf("%s", str+1);
		for (int j=1; j<=m; ++j) {
			if (str[j]=='/') add(id(i, j+1), id(i+1, j), 0), add(id(i, j), id(i+1, j+1), 1);
			else add(id(i, j), id(i+1, j+1), 0), add(id(i, j+1), id(i+1, j), 1);
		}
	}
	if ((n+m)&1) {printf("NO SOLUTION\n"); return 0; }
	memset(d, 0x3f, sizeof d);
	q[++qt]=(node) {id(1,1), d[id(1,1)]=0}; push_heap(q+1, q+qt+1);
	while (qt) {
		register node now=q[1]; pop_heap(q+1, q+qt+1), --qt;
		if (v[now.t]) continue; v[now.t]=true;
		for (int i=head[now.t]; i; i=nex[i]) if (d[now.t] + w[i] < d[to[i]]) {
			d[to[i]]= d[now.t]+ w[i], q[++qt]=(node) {to[i], d[to[i]]}, push_heap(q+1, q+qt+1);
		}
	}
	printf("%d\n", d[id(n+1, m+1)]);
	return 0;
}