6.20校内考试整理——大美江湖&&腐草为萤&&锦鲤抄题解

先安利一下题目作者：一扶苏一

先看第一题：

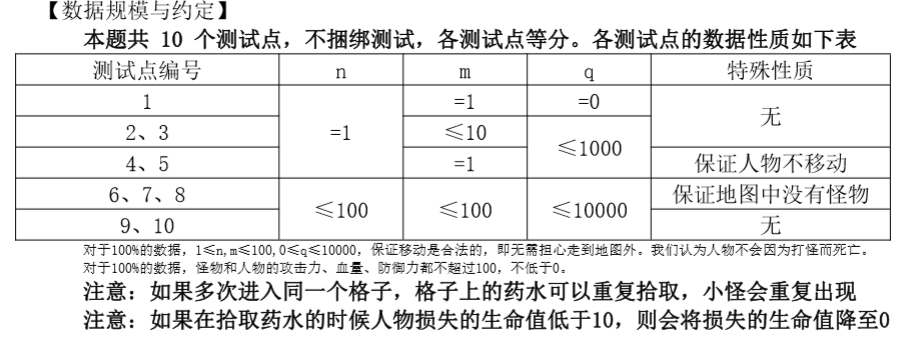
　　　　这道题就是一道简单的模拟题，只要不管一开始的位置，模拟移动与格子对应的触发事件就行了。话不多说，看代码：

 #include<iostream>
 #include<cstdio>
 #include<cctype>
 #include<cmath>

 using namespace std;

 int n,m,myst,myde,hisst,hisde,hishp,lshp,ans,stax,stay;
 int wyx[]={,,,-,+},wyy[]={,-,,,};//位移增量 

 char mp[][],ch;

 inline int read()
 {
     ans=;
     ch=getchar();
     while(!isdigit(ch)) ch=getchar();
     while(isdigit(ch)) ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
     return ans;
 }

 int main()
 {
     freopen("mzq.in","r",stdin);
     freopen("mzq.out","w",stdout);
     n=read(),m=read();
     for(int i=;i<=n;i++)
         scanf("%s",mp[i]+);
     hishp=read(),hisst=read(),hisde=read();
     stax=read(),stay=read();//目前位置
     myst=read(),myde=read();
     int q,a,b;
     q=read();
     while(q--)
     {
         a=read();
         if(a==)//查询操作
         {
             printf("%d %d %d\n",lshp,myst,myde);
         }
         else
         {
             b=read();
             stax+=wyx[b];stay+=wyy[b];//模拟移动
             switch(mp[stax][stay])//模拟触发事件
             {
                 case '.':break;
                 case 'R':
                         lshp-=;
                         if(lshp<) lshp=;
                         break;
                 case 'Q':myst+=;break;
                 case 'Y':myde+=;break;
                 case 'M':lshp+=max(,(int)ceil(hishp/(double)max(,myst-hisde)))*max(,hisst-myde);
                         break;
             }
         }
     }
     return ;
 } 

再看第二题：

　　爆搜显然是得不了全分的。我们从最简单的情况看起:

　　假如一棵树只有一个根节点u，那么答案就是u^T；

　　如果 u 只有一个孩子 v，那么要么选 u 不选 u 的子孙，要么不选 u。不妨设以节点x为根的树的答案为fx，则不选 u 的答案即为 fv，选 u 的答案即为 u^T。两种情况加起来就是 fu；

　　如果 u 有两个孩子 x,y。考虑要么选 u，要么只选 x 的子树内的元素，要么 只选 y 的子树内的元素，要么既选 x 内的元素又选 y 内的元素但不选 u。设 s 是 x 子树内的某个集合。考虑无论在y 的子树内怎么选，再加上 s 都是合法的，因为 y 和 x 之间没有祖先后代关系且 s 在 x 之内。设 g_u 是以 u 为根能选择的集合个数，那么一共有 g_y 个 集合选择 s 以后依旧合法，设 s 的权值和为 Ws，于是 s 的贡献即为 Ws×g_y。由于 fx 为 x 子树内所有可能集合的权值和，所以可以发现在以x为根的子树里所有集合s的权值和为fx。于是 x 子树内的集合对答案的总贡献是 fx×g_y。同理，y 子树内的集合对答案的贡献是 fy×g_x。 于是 fu=fy×gx+fx×gy+fx+fy+uT。gu=gx×gy+gx+gy+1。

　　考虑u又有一个孩子z,那么可以把u前面的孩子看做一个子树（仔细想一下f和g的含义，这样看成整体后可以包括在前面儿子选择的所有情况，而这个整体的f即为上文中关于f的式子不加根u^T的情况，g就是上文不加1的情况），那么情况就同上面第三种情况了。

　　见std标程：

 #include<iostream>
 #include<cstdio>
 #define int long long int 

 namespace IPT {
   const int L = ;
   char buf[L], *front=buf, *end=buf;
   char GetChar() {
     if (front == end) {
       end = buf + fread(front = buf, , L, stdin);
       if (front == end) return -;
     }
     return *(front++);
   }
 }

 template <typename T>
 inline void qr(T &x) {
   char ch = IPT::GetChar(), lst = ' ';
   while ((ch > '') || (ch < '')) lst = ch, ch=IPT::GetChar();
   while ((ch >= '') && (ch <= '')) x = (x << ) + (x << ) + (ch ^ ), ch = IPT::GetChar();
   if (lst == '-') x = -x;
 }

 struct Node{
     int nxt,to;
 }e[<<];
 int head[<<];
 int cnt;
 int n,T;
 int f[];
 int g[];
 int w[];
 const int Mod=;
 inline void addedge(int u,int v){
     e[++cnt].nxt=head[u];
     e[cnt].to=v;
     head[u]=cnt;
 }
 inline void dfs(int x,int fa){
     for(register int i=head[x];i;i=e[i].nxt){
         int v=e[i].to;
         if(v==fa) continue;
         dfs(v,x);
         f[x]=(f[x]*g[v]+f[v]*g[x]+f[v]+f[x])%Mod;
         g[x]=(g[x]*g[v]+g[x]+g[v])%Mod;
     }
     f[x]=(f[x]+w[x])%Mod;
     g[x]=(g[x]+)%Mod;
 }
 signed main(){
     freopen("dzy.in","r",stdin);
     freopen("dzy.out","w",stdout);
     qr(n); qr(T);
     for(register int i=;i<=n;i++) w[i]=T==?i:;
     for(register int i=;i<=n-;i++){
         int x = ,y = ;
         qr(x); qr(y);
         addedge(x,y);
         addedge(y,x);
     }
     dfs(,);
     std::cout<<f[]<<std::endl;
     return ;
 }

再看第三题：

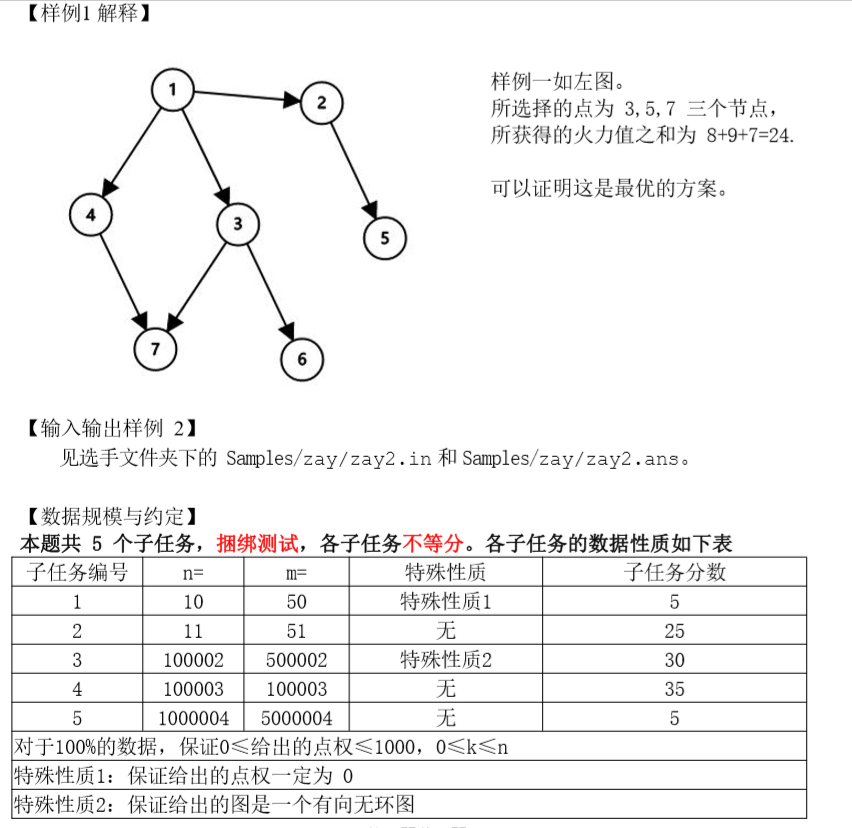
(Tip:捆绑测试就是一个子任务由若干个满足子任务要求的测试点组成，只有一个子任务下所有的测试点都过了，才能拿到全分，否则一分不给。）

　　由于题目中隐隐表达出了一种对每个点的入度的执念，便联想到了拓补排序。爆搜显然拿不到全分了，还是好好分析题目吧。先从简单的情况——DAG开始。对于一个DAG（有向无环图），一定至少有一个拓补排序。所以对一个DAG，除了一开始就入度为0的点，其他点都能通过逆序的拓补排序选上，所以只要把一开始入度不为零的点从大到小排个序，选前k个就行。

　　对于一个有环的图呢？可以考虑对一个强联通分量“缩点”来转化成DAG的情况，即把一个环看做一个点，那么整张图就可看成一个DAG。这时选点的情况就有两种：一是对整张图的选点，二是对单独一个环里的选点。第一种在上面已经考虑一部分了，这里考虑第二种：一个环如果没有外面的点连向他，即没有入度，那么这个环最少要剩一个点，其他点都可以通过环的搜索树的逆序选上，不妨让环中权值最小的点当那个剩下的点，这样可使局部最优。如果有入度，那么环中的点就有可能都被选。

　　由上，可知对能被选到的点（DAG中一开始入度不为零的点、环中能被选上的点）排个序，再找前k个就行了。进行一次 tarjan（找环算法）的复杂度是 O(n+m)，选前 k 个点可以排序一下。这样总复杂 度 O(m+nlogn)。注意到复杂度瓶颈在排序上，考虑我们只需要前 k 大而不需要具体前 k 个之间的大小关系，于是使用 std::nth_element()函数可 以将复杂度降至 O(n+m)。期望得分 40 分。注意，输入规模到了 107 级别，需要 fread 来实现读入优化。

见STD代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<string>
 #include<queue>
 namespace IPT {
   const int L = ;
   char buf[L], *front=buf, *end=buf;
   char GetChar() {
     if (front == end) {
       end = buf + fread(front = buf, , L, stdin);
       if (front == end) return -;
     }
     return *(front++);
   }
 }

 template <typename T>
 inline void qread(T &x) {
   char ch = IPT::GetChar(), lst = ' ';
   while ((ch > '') || (ch < '')) lst = ch, ch=IPT::GetChar();
   while ((ch >= '') && (ch <= '')) x = (x << ) + (x << ) + (ch ^ ), ch = IPT::GetChar();
   if (lst == '-') x = -x;
 }

 template<typename sp>
 inline sp mmax(sp a,sp b){
     return a>b?a:b;
 }
 template<typename sp>
 inline sp mmin(sp a,sp b){
     return a>b?b:a;
 }
 struct Node{
     int nxt,from,to;
 }e[];
 int n,m,k,rd[];
 int dfn[],low[],p[];
 int head[],cnt,top,s[],sta[];
 int tim;
 bool vis[];
 int minp[];
 int ans;
 void tarjan(int x){
     dfn[x]=low[x]=++tim;
     vis[x]=true;
     sta[++top]=x;
     for(register int i=head[x];i;i=e[i].nxt){
         int v=e[i].to;
         if(!dfn[v]){
             tarjan(v);
             low[x]=mmin(low[x],low[v]);
         }
         else if(vis[v]) low[x]=mmin(low[x],dfn[v]);
     }
     if(dfn[x]==low[x]){
         while(true){
             int y=sta[top--];
             s[y]=x;
             vis[y]=false;
             if(p[y]<p[minp[x]])  minp[x]=y;
             if(x==y) break;
         }
     }
 }
 inline void addedge(int u,int v){
     e[++cnt].nxt=head[u];
     e[cnt].from=u;
     e[cnt].to=v;
     head[u]=cnt;
 }
 int main(){
     freopen("zay.in","r",stdin);
     freopen("zay.out","w",stdout);
     qread(n);qread(m);qread(k);
     for(register int i=;i<=n;i++) qread(p[i]);
     for(register int i=;i<=n;i++) minp[i]=i;
     for(register int i=;i<=m;i++){
         int x=,y=;
         qread(x);qread(y);
         addedge(x,y);
     }
     for(register int i=;i<=n;i++){
         if(!dfn[i]) tarjan(i);
     }
     for(register int i=;i<=m;i++){
         int u=s[e[i].from],v=s[e[i].to];
         if(u==v) continue;
         rd[v]++;
     }
     for(register int i=;i<=n;i++) if(s[i]==i&&!rd[i]) p[minp[i]]=;
     std::sort(p+,p++n);
     //for(register int i=1;i<=n;i++) printf("%d ",p[i]);
     for(register int i=;i<=k;i++) ans+=p[n-i+];
     std::cout<<ans<<std::endl;
     return ;
 }