二、启动一款app演示

一、下载aapt包

　　1. aapt即Android Asset Packaging Tool，在SDK的build-tools目录下。该工具可以查看apk包名和launcherActivity

　　2.打开android-sdk里面双击SDK-manager,下载buidl-tools

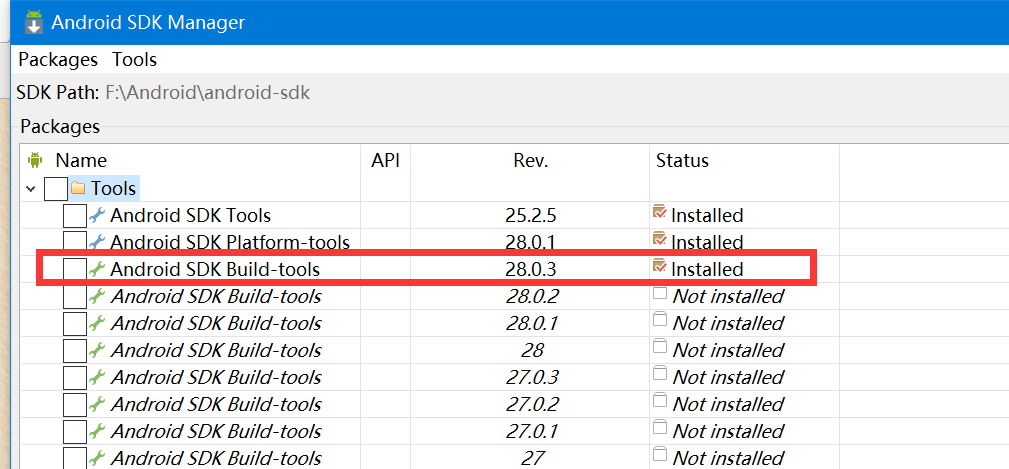
　　3.下载完成之后在 sdk路径下找到：F:\Android\android-sdk\build-tools\28.0.3下找到aapt.exe，双击运行即可

　　4.打开cmd------输入aapt回车，出现以下情况代表安装成功

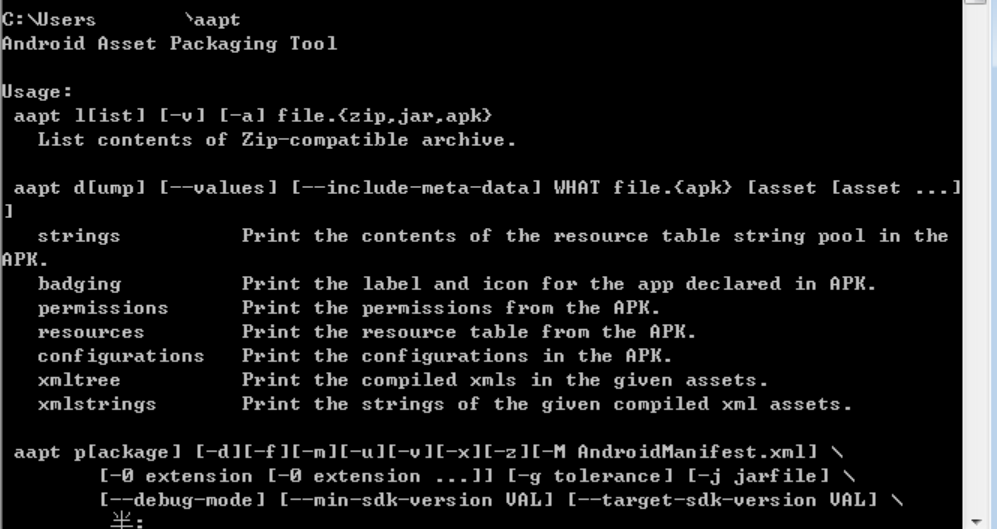
二、使用aapt获取app的包名

　　1.取将app的包放至D:\devices（xxx.apk）

　　2.aapt dump badging D:\test\xxx.apk(APK的全名，如手机淘宝.apk)

包名：

launcherActivity的值：

三、写脚本：

1.platformName：这里是android的apk

2.deviceName：手机设备名称，通过adb devices查看

3.platformVersion：android系统的版本号

4.appPackage：apk包名

5.appActivity：apk的launcherActivity

6. noReset ：False  --是否重置APP，True不重置

def test_Init(self):
        self.desired_caps = {}
        self.desired_caps['platformName'] = myConfig.getAppDevices("platform_Name")
        self.desired_caps['platformVersion'] = myConfig.getAppDevices("platform_Version")
        self.desired_caps['deviceName'] = myConfig.getAppDevices("device_Name")
        # self.desired_caps['app'] = myConfig.getAppDevices("app_Path")
        self.desired_caps['noReset'] = myConfig.getAppDevices("app_noReset")
        self.desired_caps['unicodeKeyboard'] = myConfig.getAppDevices("app_unicodeKeyBoard")
        self.desired_caps['resetKeyboard'] = myConfig.getAppDevices("app_resetKeyBoard")
        # 要启动的应用包名
        self.desired_caps['appPackage'] = myConfig.getAppDevices("app_Package")
        self.desired_caps['automationName'] = myConfig.getAppDevices("app_automationName")
        # 要启动的应用的起始activity
        self.desired_caps['appActivity'] = myConfig.getAppDevices("app_Activity")

        server_url = myConfig.getAppDevices("appium_server")+':'+myConfig.getAppDevices("appium_port")+'/wd/hub'
        # print("server_url = " + server_url)

        self.driver = webdriver.Remote(server_url,self.desired_caps)
        self.driver.implicitly_wait(30)

        return self.driver

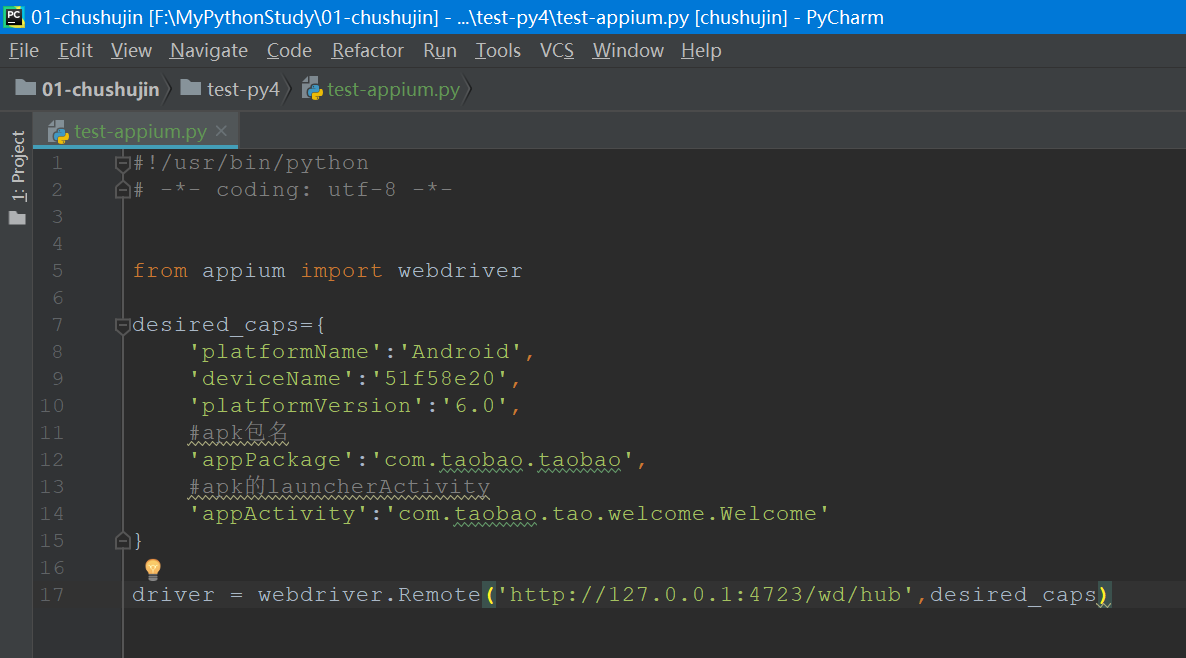
　　6.driver中的路径为

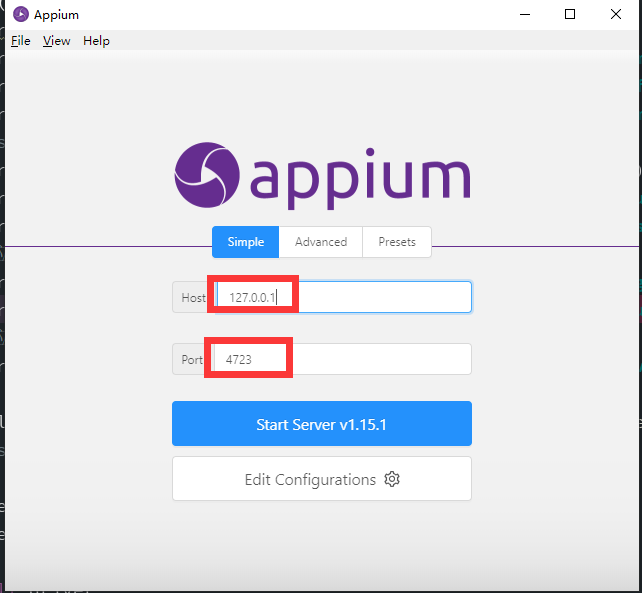
7.打开appium，点击右上角的运行按钮，变为方形的为运行中

8.确认连接手机

9.使用pycharm运行脚本

10.接下来，手机app中的手机淘宝就会启动