c++实验7 二叉树

二叉树数据结构表示及基本操作算法实现

1、所加载的库函数或常量定义及类的定义：

#include<stdlib.h>
#include<stdio.h>
#include"BiTreeNode.h"
#include<iostream>
using namespace std;
template <class T>
class BiTree
{
private:
    BiTreeNode<T> *root;            //根结点指针
    void Destroy(BiTreeNode<T>* &t);

    void InOrder(BiTreeNode<T> *&t, void (*Visit)(T item));
    void PostOrder(BiTreeNode<T>* &t, void (*Visit)(T item));
public:
    BiTree(void):root(NULL){};                 //构造函数
    ~BiTree(void){};                         //析构函数
        void PreOrder(BiTreeNode<T>* &t, void (*Visit)(T item));
    //构造二叉树
    void MakeTree(const T item, BiTree<T> &left, BiTree<T> &right);
    void Destroy(void);            //撤消二叉树

    BiTreeNode<T> *getroot()
    {
        return root;
    }
    void PreOrder(void (*Visit)(T item));        //前序遍历
    void InOrder(void (*Visit)(T item));        //中序遍历
    void PostOrder(void (*Visit)(T item));        //后序遍历
    BiTreeNode<T> *createbintree();             //前序遍历建立二叉树
    int numofnode(BiTreeNode<T> *t);            //二叉树结点个数
    void showmid(BiTreeNode<T> *t);             //按中序遍历所有子节点值
    BiTreeNode<T> *LeverCreateTree(BiTreeNode<T> *tr);//按层次遍历-非递归创建二叉树
    BiTreeNode<T> *GetTreeNode(const T item, BiTreeNode<T> *left=NULL, BiTreeNode<T> *right=NULL)
    {
        BiTreeNode<T> *p;
        p = new BiTreeNode<T> (item, left, right);
        return p;
    }
    int leafnode(BiTreeNode<T> *t);      //二叉树叶子节点个数
};

2、二叉树存储结构定义：链式存储

结点类：

template <class T>
class BiTreeNode
{
public:
    BiTreeNode<T> *leftChild;                        //左子树指针
    BiTreeNode<T> *rightChild;                        //右子树指针

    T data;                                            //数据域

    //构造函数和析构函数
    BiTreeNode():leftChild(NULL), rightChild(NULL){}
    BiTreeNode(T item, BiTreeNode<T> *left = NULL, BiTreeNode<T> *right = NULL):
        data(item), leftChild(left), rightChild(right){}
    ~BiTreeNode(){}

    BiTreeNode<T>* &Left(void)    //注意返回值类型为指针的引用类型
        {return leftChild;}
    BiTreeNode<T>* &Right(void)    //注意返回值类型为指针的引用类型
        {return rightChild;}
    BiTreeNode<T>* setleft(){}

};

3、二叉树递归遍历算法（3种）

注：已知树的根结点 和测试文件中增加visit函数 得到按三种树的序遍历（起到显示结点值作用-并不好用【第4题种自行定义了showmid函数按中序显示】）

1）     先序递归遍历

template <class T>
void BiTree<T>::PreOrder(BiTreeNode<T> *&t, void (*Visit)(T item))
//使用Visit(item)函数前序遍历二叉树t
{
    if(t != NULL)
    {
        Visit(t->data);   //根
        PreOrder(t->Left(), Visit);  //左子树
        PreOrder(t->Right(), Visit); //右子树
    }
}

2）     中序递归遍历

template <class T>
void BiTree<T>::InOrder(BiTreeNode<T> *&t, void (*Visit)(T item))
//使用Visit(item)函数中序遍历二叉树t
{
    if(t != NULL)
    {
        InOrder(t->Left(), Visit); //左子树
        Visit(t->data); //根
        InOrder(t->Right(), Visit); //右子树
    }
}

3）     后序递归遍历

template <class T>
void BiTree<T>::PostOrder(BiTreeNode<T> *&t, void (*Visit)(T item))
//使用Visit(item)函数后序遍历二叉树t
{
    if(t != NULL)
    {
        PostOrder(t->Left(), Visit); //左子树
        PostOrder(t->Right(), Visit); //右子树
        Visit(t->data); //根
    }
}

测试数据：

#include <iostream>
#include<stdlib.h>
#include"BiTree.h"
using namespace std;
template <class T>
void Visit(T item)
{
    cout << item << "   ";
}
int main()
{
    BiTree<char>a,b,c,d,e,f,g,null;
    g.MakeTree('G',null,null);
    d.MakeTree('D',null,g);
    b.MakeTree('B',d,null);
    e.MakeTree('E',null,null);
    f.MakeTree('F',null,null);
    c.MakeTree('C',e,f);
    a.MakeTree('A',b,c);
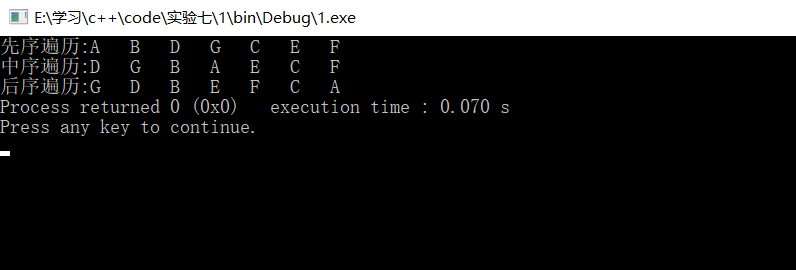
    cout<<"先序遍历:";
    a.PreOrder(Visit);
    cout<<"\n中序遍历:";
    a.InOrder(Visit);
    cout<<"\n后序遍历:";
    a.PostOrder(Visit);
    return ;
}

结果：

4、二叉树创建递归算法-选用（前序）遍历实现二叉树创建的递归算法

注：按先序遍历创建二叉树（#为空结点）

template <class T>
BiTreeNode<T> * BiTree<T>:: createbintree()
{ /*按照前序遍历的顺序建立一棵给定的二叉树*/
    char ch;
    BiTreeNode<T> * t;
    if ((ch=getchar())=='#')
        t=NULL;
    else
        {
            t = new BiTreeNode<T>;
            t->data=ch;
            t->leftChild=createbintree();
            t->rightChild=createbintree();
        }

    return t;
}
template <class T>
void BiTree<T>::showmid(BiTreeNode<T> *t)
{
    if(t!=NULL&&t->leftChild!=NULL)
        showmid(t->leftChild);
    cout<<t->data<<" ";
    if(t!=NULL&&t->rightChild!=NULL)
        showmid(t->rightChild);
}

———— 其中增加showmid方法 显示给出结点下所有结点的值（按中序排列）

测试数据：

int main()
{
      BiTree<char> a;
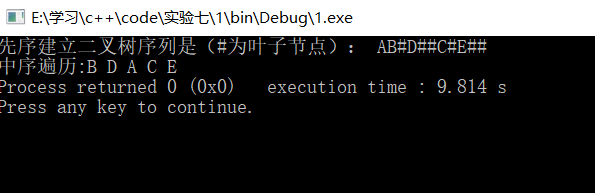
    cout<<"先序建立二叉树序列是（#为叶子节点）： ";
    BiTreeNode<char> * b= a.createbintree();
    cout<<"中序遍历:";
    a.showmid(b);
    return ;
}

结果

5、按层次遍历写出二叉树创建的非递归算法

注：已知树的根结点 按层输入二叉树（即按满树从上到下从左到右输入各结点值 #表示空结点 @为结束标志）

template<class T>
BiTreeNode<T> *BiTree<T>::LeverCreateTree(BiTreeNode<T> *tr)//按层次遍历-非递归创建二叉树
//输入序列：扩展结点度为2
{
    BiTreeNode<T> *q[],*p,*k;//q为队列，
    int f=,w=,n=;//f表示队头，w表示队尾。n为计数器
    char ch;
    cin>>ch;
    if (ch=='#'||ch=='@') tr=NULL;//空树时
    else{//
            tr=new BiTreeNode<T>;//二叉树根结点的创建
            tr->data=ch;
            tr->leftChild=NULL;//
            tr->rightChild=NULL;//
            q[w++]=tr;
            cin>>ch;
            while(ch!='@')
            {
                n=n%;
                if (ch!='#')
                {
                    p=new BiTreeNode<T>;
                    p->data=ch;
                    p->leftChild=NULL;
                    p->rightChild=NULL;
                    q[w++]=p;
                }
                else
                {p=NULL;}
                n++;
                if (n==)
                    {k=q[f];k->leftChild=p;}
                else if(n==)
                    {k=q[f++];k->rightChild=p;}
                cin>>ch;
            }//while
        }//
    return tr;
}//LeverCreateTree

测试数据

int main()
{
    BiTree<char> A;
    BiTreeNode<char>* b;
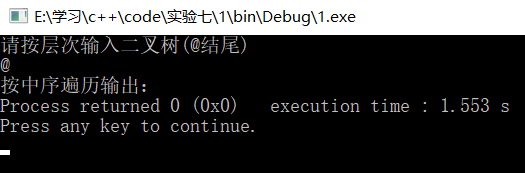
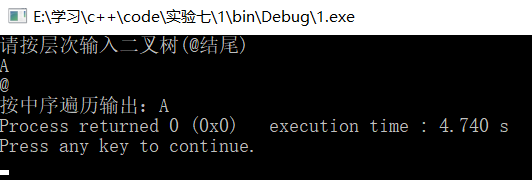
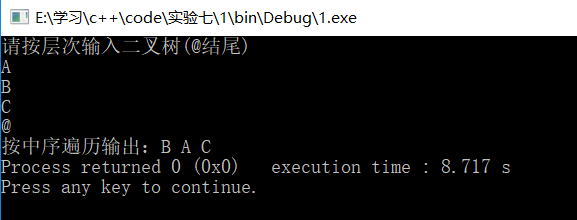
    cout<<"请按层次输入二叉树(@结尾)"<<endl;
    BiTreeNode<char>* c=A.LeverCreateTree(b);
    cout<<"按中序遍历输出：";
    A.showmid(c);
    return ;
}

结果：

1）空树

2）仅有一个结点树

3）一般的普通的二叉树

4）给出数据输入的序列。

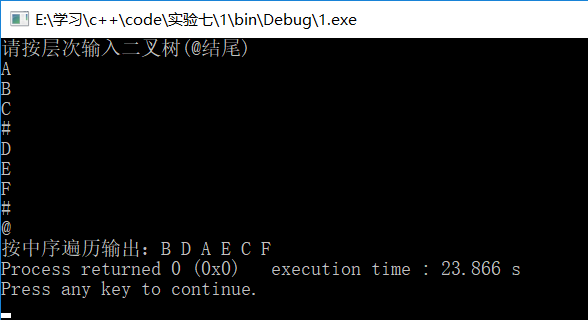
试分析，上列算法的基本算法思想，试问//99这句没有，数据的输入序列应如何？

去掉//99语句后：

　　理论上必须输入序列至少2层（1层即只有根结点）否则下方的左右子树不明确

　　但实际试验后没区别！！　　

若有个人思路见解望请留言指正

6、求二叉树的深度递归算法

注：已知树的根结点 得到二叉树深度

template <class T> //二叉树的深度方法
int PostTreeDepth(BiTreeNode<T> *t)
{
    int hl=,hr=;
    if (t==NULL)      return ;
    hl=PostTreeDepth(t->Left());
    hr=PostTreeDepth(t->Right());
   if (hl>hr)
       return (hl+);
   else
       return (hr+);
}

7、求二叉树的结点数递归算法

注：已知树的根结点 得到二叉树结点个数

template <class T>
int BiTree<T>::numofnode(BiTreeNode<T> *t)  //二叉树结点个数
{
    if (t==NULL)
        return ;    //递归出口
    else
        return( numofnode(t->leftChild)+numofnode(t->rightChild) + );
}

8、求二叉树的叶子数递归算法

注：已知树的根结点 得到二叉树叶子节点个数

template <class T>
int BiTree<T>::leafnode(BiTreeNode<T> *t)//二叉树叶子节点个数
{
    if(t==NULL)
        return ;    //递归出口
    else if (t->leftChild==NULL && t->rightChild==NULL)
        return ;    //递归出口
    else
        return(leafnode(t->leftChild)+leafnode(t->rightChild));
}

此处对上面3问进行测试

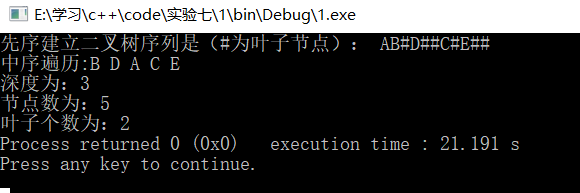
9、求两颗二叉树的相似

递归算法提示：

1）若T1和T2均为空，则返回值为1；

2）若T1和T2的深度均为1（即只有一个结点），则返回为1；

3）若T1的左子树和T2的左子树相似，并且T1的右子树和T2的右子树相似，则返回为1;

4)其它为返回值为0；

注：已知2个根节点 得到是否两树相似 （该段不写于BiTree类中）

template <class T>
int islike(BiTreeNode<T> * t1,  BiTreeNode<T> * t2)
{
    int t=;
    if(t1==NULL && t2==NULL)
        t=;
    else if(PostTreeDepth(t1)==PostTreeDepth(t2)&&PostTreeDepth(t1)==)
        t=;
    else if((islike(t1->leftChild,t2->leftChild)==)&&(islike(t1->rightChild,t2->rightChild)==))
        t=;
    else
        t=;
    return t;
}

测试结果：

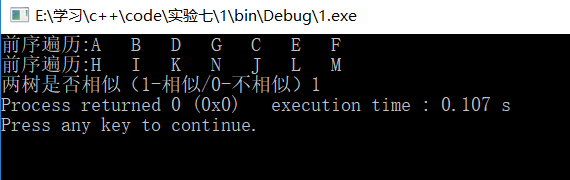
8