Pregel的应用实例——单源最短路径
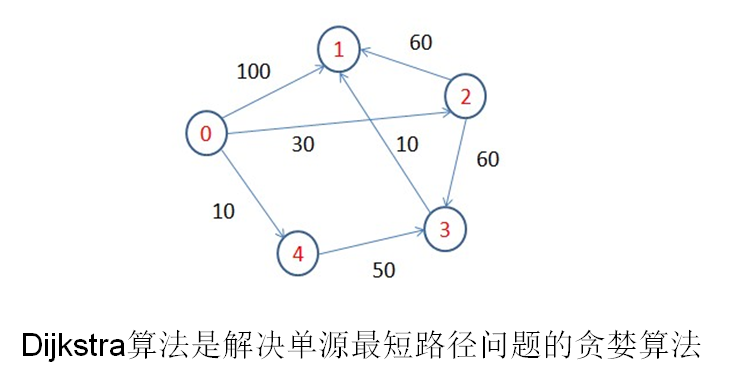

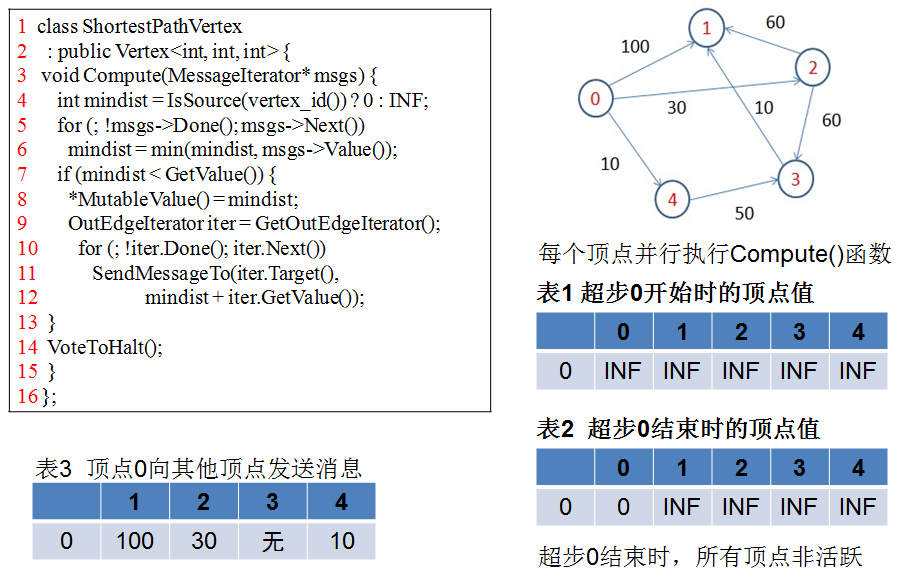
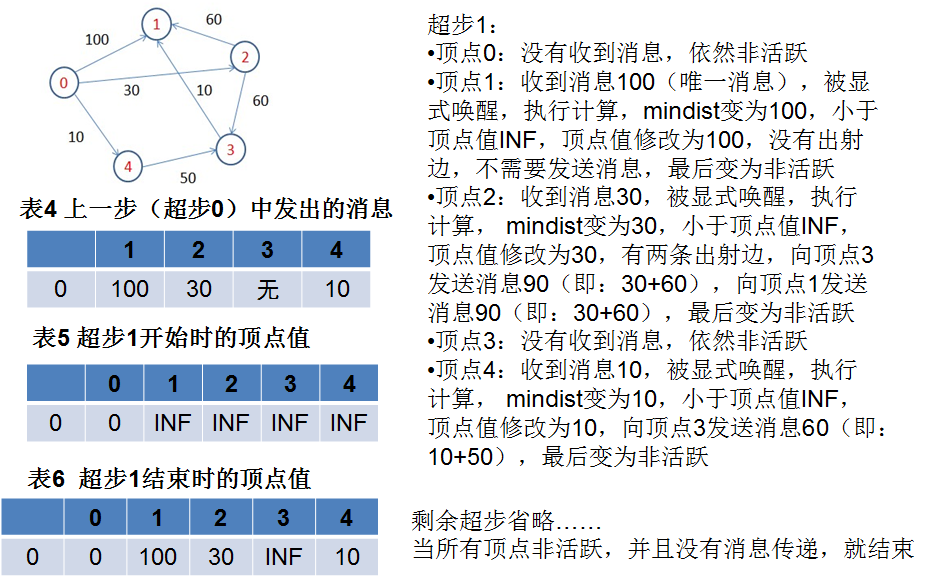
Pregel的应用实例——单源最短路径的更多相关文章
- 【算法导论】单源最短路径之Bellman-Ford算法
单源最短路径指的是从一个顶点到其它顶点的具有最小权值的路径.我们之前提到的广度优先搜索算法就是一种无权图上执行的最短路径算法,即在所有的边都具有单位权值的图的一种算法.单源最短路径算法可以解决图中任意 ...
- Dijkstra算法详细(单源最短路径算法)
介绍 对于dijkstra算法,很多人可能感觉熟悉而又陌生,可能大部分人比较了解bfs和dfs,而对dijkstra和floyd算法可能知道大概是图论中的某个算法,但是可能不清楚其中的作用和原理,又或 ...
- Dijkstra 单源最短路径算法
Dijkstra 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法,由计算机科学家 Edsger Dijkstra 于 1956 年 ...
- Bellman-Ford 单源最短路径算法
Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法.该算法由 Richard Bellman 和 Leste ...
- 洛谷P3371 【模板】单源最短路径
P3371 [模板]单源最短路径 282通过 1.1K提交 题目提供者HansBug 标签 难度普及/提高- 提交 讨论 题解 最新讨论 不萌也是新,老司机求带 求看,spfa跑模板40分 为什么 ...
- 单源最短路径算法---Dijkstra
Dijkstra算法树解决有向图G=(V,E)上带权的单源最短路径问题,但是要求所有边的权值非负. 解题思路: V表示有向图的所有顶点集合,S表示那么一些顶点结合,从源点s到该集合中的顶点的最终最短路 ...
- Til the Cows Come Home(poj 2387 Dijkstra算法(单源最短路径))
Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 32824 Accepted: 11098 Description Bes ...
- 单源最短路径——dijkstra算法
dijkstra算法与prim算法的区别 1.先说说prim算法的思想: 众所周知,prim算法是一个最小生成树算法,它运用的是贪心原理(在这里不再证明),设置两个点集合,一个集合为要求的生成树的 ...
- 【转】Dijkstra算法(单源最短路径)
原文:http://www.cnblogs.com/dolphin0520/archive/2011/08/26/2155202.html 单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路 ...
随机推荐
- 38-python基础-python3-检查字典中是否存在键或值
in 和 not in 操作符 请注意, 在前面的例子中,‘name’ in spam 本质上是一个简写版本.相当于'name' in spam.keys()
- im开发总结:netty的使用
最近公司在做一个im群聊的开发,技术使用得非常多,各种代码封装得也是十分优美,使用到了netty,zookeeper,redis,线程池·,mongdb,lua,等系列的技术 netty是对nio的一 ...
- Pytest conftest共享数据及不同层次共享
数据共享:在 conftest.py配置里写方 法可以实现数据共享, 不需要import导入.可 以跨文件共享 1.建立一个新的文件,文件名必须叫"conftest.py",然后写 ...
- CG-CTF pwn部分wp
面向pwn刷cgctfPWN1,When did you born题目给了一个ELF文件,和一个.C文件先运行ELF,大概如下What’s Your Birth?0What’s Your Name?0 ...
- android中读取SD卡上的数据
通过Context的openFileInput或者openFileOutput打开的文件输入输出流是操作应用程序的数据文件夹里的文件,这样存储的大小比较有限,为了更好的存取应用程序的大文件数据,应用程 ...
- 人生苦短,我学PYTHON
人生苦短我学PYTHON 坚持 努力
- JNI原理与静态、动态注册
前言 JNI不仅仅在NDK开发中应用,它更是Android系统中Java与Native交互的桥梁,不理解JNI的话,你就只能停留在Java Framework层.这一个系列我们来一起深入学习JNI. ...
- KiCAD绘制器件内部逻辑符号库
KiCAD绘制器件内部逻辑符号库 像比较器,运放这些器件,里面是由多个相同的part组成,有时候我们只需要用到其中一个或者某几个,又或者是为了在原理图中更清楚的表达出逻辑关系,需要单独绘制内部的逻辑符 ...
- 视频专家之路【三】:Vs开发环境的搭建
本文是听了雷宵骅大神的课之后的总结,部分内容借用了其PPT的内容,如有侵权请告知删除. 雷宵骅大神的博客为:https://blog.csdn.net/leixiaohua1020 这里提及一点,原来 ...
- svn中的trunk,branch和tags(转)
转自:https://www.cnblogs.com/keyi/p/5953649.html 我相信初学开发在SVN作为版本管理时,都估计没可能考虑到如何灵活的运用SVN来管理开发代码的版本,下面我 ...
