Codeforces Round #564 (Div. 2) D. Nauuo and Circle（树形DP）

D. Nauuo and Circle

•参考资料

　　[1]:https://www.cnblogs.com/wyxdrqc/p/10990378.html

•题意

　　给出你一个包含 n 个点的树，这 n 个点编号为 1~n；

　　给出一个圆，圆上放置 n 个位置，第 i 个位置对应树中的某个节点，并且不重复；

　　求在圆上还原这棵树后，使得边不相交的总方案数；

•题解

　　

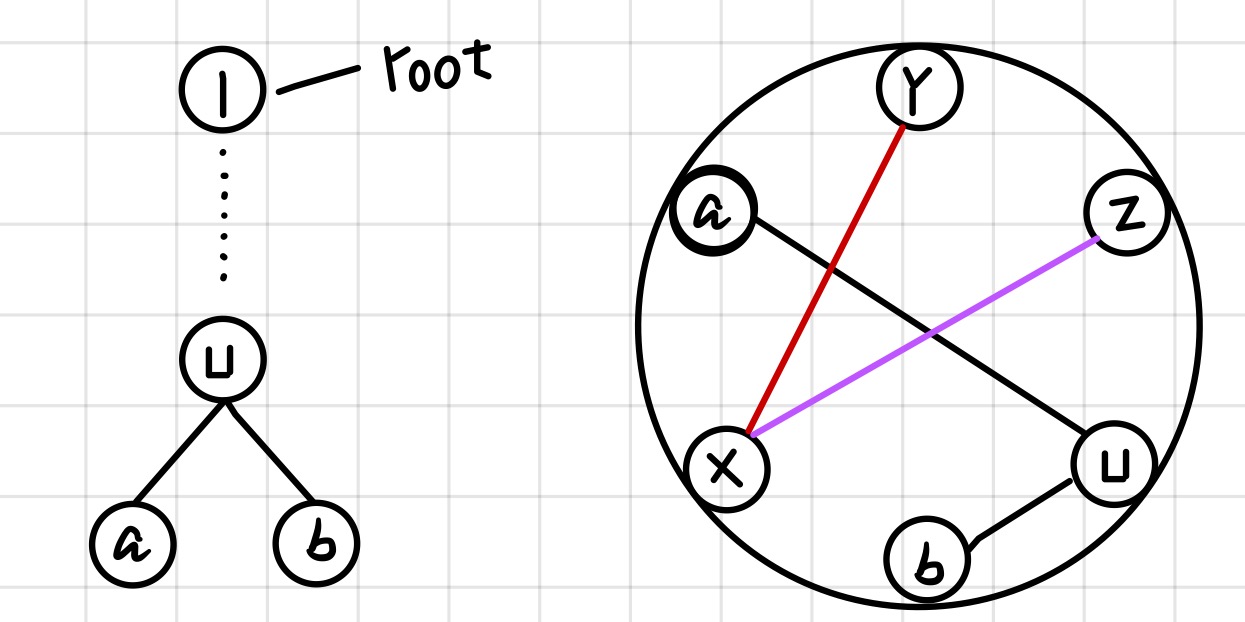
　　①为何每一颗子树一定是连续的一段圆弧？

　　　　假设不是连续的圆弧，如图所示：

　　　　

　　　　为了使 x 接到树上，必然会有 x-y 或 x-z 相连的边，这样就会出现交点；

　　②对于以 u 为根的子树，假设 u 有两个儿子 a,b，那么，需要找连续的 x+y+1 个位置放置这些节点；

　　　　

　　　　（x:以a为根节点的子树节点个数，y:以b为根节点的子数的节点个数）

　　　　也就是图中的sum₁,sum₂,sum₃位置；

　　　　u可以放在这三个位置的任意一个位置，a 从剩余的两个位置中选，b只有一个位置可选；

　　　　总的方案数为 3!；

　　　　但是每个方案中 a,b 都有排列方案，故需要乘上 f_a×f_b；

　　　　对于树的根节点 1，一共有 n 个位置可放，求出其中一个的方案数 f₁，答案就是 n×f₁；

•Code

 #include<bits/stdc++.h>
 using namespace std;
 #define ll long long
 #define memF(a,b,n) for(int i=0;i <= n;a[i++]=b);
 const int maxn=2e5+;
 const int MOD=;

 int n;
 int num;
 int head[maxn];
 struct Edge
 {
     int to,next;
 }G[maxn<<];
 void addEdge(int u,int v)
 {
     G[num]=Edge{v,head[u]};
     head[u]=num++;
 }
 ll fact[maxn];
 ll dp[maxn];///与f函数功能相同
 vector<int >son[maxn];
 void DFS(int u,int f)
 {
     for(int i=head[u];~i;i=G[i].next)
     {
         int v=G[i].to;
         if(v == f)
             continue;

         son[u].push_back(v);
         DFS(v,u);
     }

     int k=son[u].size()+(u !=  ? :);///如果u=1就不用再找u可放置的位置，因为1已经被固定了
     dp[u]=fact[k];
     for(int i=;i < son[u].size();++i)
         dp[u]=dp[u]*dp[son[u][i]]%MOD;
 }
 ll Solve()
 {
     for(int i=;i <= n;++i)
         son[i].clear();

     DFS(,);

     return dp[]*n%MOD;
 }
 void Init()
 {
     num=;
     memF(head,-,n);
     fact[]=;
     for(int i=;i <= n;++i)
         fact[i]=(i*fact[i-])%MOD;
 }
 int main()
 {
     scanf("%d",&n);
     Init();
     for(int i=;i < n;++i)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         addEdge(u,v);
         addEdge(v,u);
     }
     printf("%lld\n",Solve());
     return ;
 }