11_数据降维PCA
1.sklearn降维API:sklearn. decomposition
2.PCA是什么:主成分分析
本质:PCA是一种分析、简化数据集的技术。
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量。
当特征达到上百的时候,考虑是否要使用PCA来删除部分特征。
3.高维度数据容易出现的问题:特征之间通常是线性相关的。
4.PCA语法:
PCA(n_components=None) 将数据分解为较低维数空间
n_components:可以是小数,也可以是整数。为小数时,指定保存多少的数据量,通常是0.9~0.95,表示保存90%到95%的数据量。
为整数时,表示减少到多少特征数量,一般不使用整数。
PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features] 返回值:转换后指定维度的array
5.PCA演示过程:
1.初始化PCA,指定减少后的维度。
2.调用fit_transform
案例:
def pca():
"""
主成分分析进行特征降维
:return:
"""
pca = PCA(n_components=0.9)
data = pca.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
print(data) if __name__ == '__main__':
# normalization()
# stand()
# im()
# var()
pca()
结果:
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
6.简单的降维过程:
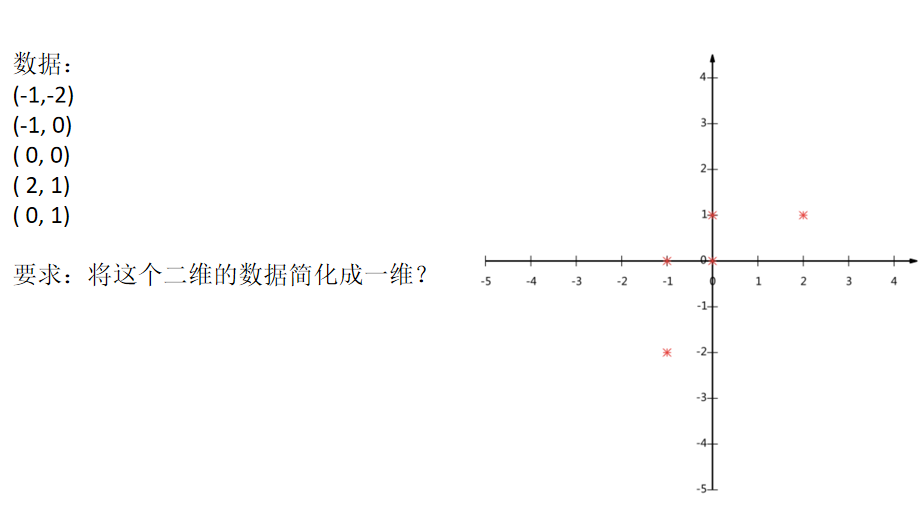
可以投向x轴和y轴,但是会丢失数据点,五个点变成三个点。
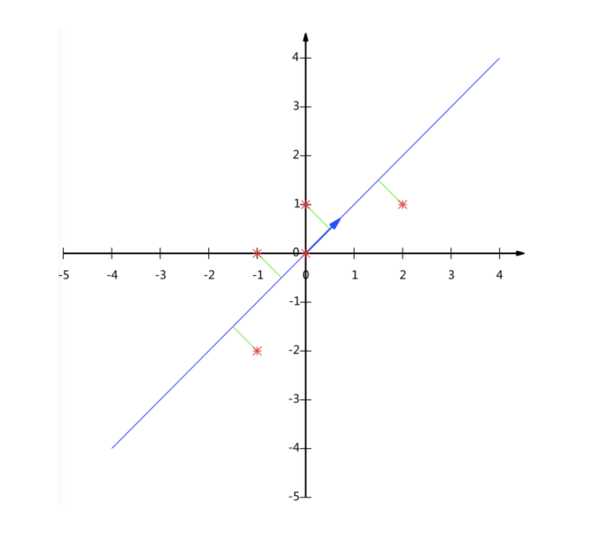

11_数据降维PCA的更多相关文章
- 数据降维-PCA主成分分析
1.什么是PCA? PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法.PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特 ...
- 数据降维PCA——学习笔记
PCA主成分分析 无监督学习 使方差(数据离散量)最大,更易于分类. 可以对隐私数据PCA,数据加密. 基变换 投影->内积 基变换 正交的基,两个向量垂直(内积为0,线性无关) 先将基化成各维 ...
- SIGAI机器学习第八集 数据降维1
讲授数据降维原理,PCA的核心思想,计算投影矩阵,投影算法的完整流程,非线性降维技术,流行学习的概念,局部线性嵌入,拉普拉斯特征映射,局部保持投影,等距映射,实际应用 大纲: 数据降维问题PCA的思想 ...
- [机器学习]-PCA数据降维:从代码到原理的深入解析
&*&:2017/6/16update,最近几天发现阅读这篇文章的朋友比较多,自己阅读发现,部分内容出现了问题,进行了更新. 一.什么是PCA:摘用一下百度百科的解释 PCA(Prin ...
- 主成分分析PCA数据降维原理及python应用(葡萄酒案例分析)
目录 主成分分析(PCA)——以葡萄酒数据集分类为例 1.认识PCA (1)简介 (2)方法步骤 2.提取主成分 3.主成分方差可视化 4.特征变换 5.数据分类结果 6.完整代码 总结: 1.认识P ...
- 降维PCA技术
降维技术使得数据变得更易使用,并且它们往往能够去除数据中的噪声,使得机器学习任务往往更加精确. 降维往往作为预处理步骤,在数据应用到其它算法之前清洗数据.有很多技术可以用于数据降维,在这些技术中,独立 ...
- Coursera《machine learning》--(14)数据降维
本笔记为Coursera在线课程<Machine Learning>中的数据降维章节的笔记. 十四.降维 (Dimensionality Reduction) 14.1 动机一:数据压缩 ...
- 数据降维技术(2)—奇异值分解(SVD)
上一篇文章讲了PCA的数据原理,明白了PCA主要的思想及使用PCA做数据降维的步骤,本文我们详细探讨下另一种数据降维技术—奇异值分解(SVD). 在介绍奇异值分解前,先谈谈这个比较奇怪的名字:奇异值分 ...
- 第七篇:数据预处理(四) - 数据归约(PCA/EFA为例)
前言 这部分也许是数据预处理最为关键的一个阶段. 如何对数据降维是一个很有挑战,很有深度的话题,很多理论书本均有详细深入的讲解分析. 本文仅介绍主成分分析法(PCA)和探索性因子分析法(EFA),并给 ...
随机推荐
- vue 项目 去哪儿
去哪儿项目 使用vue +vue-router+vuex +axios完成,包括3个部分内容 1.首页演示,包括首页header,首页轮播图,周末去哪儿,热销推荐开发 2.城市列表页面开发 ,包括城市 ...
- php 三种文件下载的实现
第一种:直接添加文件下载的绝对路径连接 //如:我有一个文件在demo.xx.cn/demo.zip <button> <a href = "http://demo.xx. ...
- [SNOI 2017] 炸弹
题目描述: 给定炸弹和爆炸范围,求对于每个炸弹连锁爆炸的炸弹总和对\(1e9+7\)取膜 思路: 为啥都是线段树+TS+tarjan呢? 实在是搞不懂~~ 线性\(O(n)\)递推即可. #inclu ...
- 什么是存根类 Stub
转:http://www.cnblogs.com/cy163/archive/2009/08/04/1539077.html 存根类是一个类,它实现了一个接口,但是实现后的每个方法都是空的. ...
- CSS3视口单位vw,wh
vw和vh是视口(viewport units)单位,何谓视口,就是根据你浏览器窗口的大小的单位,不受显示器分辨率的影响,是不是很神奇,这就代表了,我们不需要顾虑到现在那么多不同电脑有关分辨率的自适应 ...
- vue-router 基本操作
安装 vue-router 在命令行中进入 vue 的项目目录里,运行命令 npm install vue-router --save 来进行安装 npm install vue-router - ...
- day 56 Django基础五之django模型层(二)多表操作
Django基础五之django模型层(二)多表操作 本节目录 一 创建模型 二 添加表记录 三 基于对象的跨表查询 四 基于双下划线的跨表查询 五 聚合查询.分组查询.F查询和Q查询 六 ORM ...
- seienium基础(测试脚本中的等待方法)
测试脚本中的等待方法 一.加等待时间的目的 等待是为了使脚本执行更加稳定 二.常用的休眠方式 第一种 sleep(): 设置固定休眠时间.python 的 time 包提供了休眠方法 sleep() ...
- 2019-5-15-影子系统让-C++-程序无法运行
title author date CreateTime categories 影子系统让 C++ 程序无法运行 lindexi 2019-05-15 15:24:35 +0800 2019-05-1 ...
- T2980 LR棋盘【Dp+空间/时间优化】
Online Judge:未知 Label:Dp+滚动+前缀和优化 题目描述 有一个长度为1*n的棋盘,有一些棋子在上面,标记为L和R. 每次操作可以把标记为L的棋子,向左移动一格,把标记为R的棋子, ...
