洛谷P3335 [ZJOI2013]蚂蚁寻路

题目描述

在一个 n*m 的棋盘上，每个格子有一个权值，初始时，在某个格子的顶点处一只面朝北的蚂蚁，我们只知道它的行走路线是如何转弯，却不知道每次转弯前走了多长。

蚂蚁转弯是有一定特点的，即它的转弯序列一定是如下的形式：右转，右转，左转，左转，右转，右转…左转，左转，右转，右转，右转。即两次右转和两次左转交替出现的形式，最后两次右转（最后两次一定是右转）后再多加一次右转。我们还知道，蚂蚁不会在同一个位置连续旋转两次，并且蚂蚁行走的路径除了起点以外，不会到达同一个点多次，它最后一定是回到起点然后结束自己的行程，而且蚂蚁只会在棋盘格子的顶点处转弯。

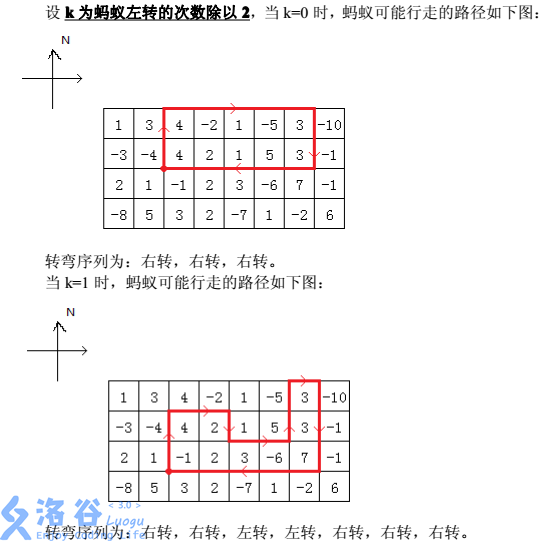
现在已知棋盘大小、每个格子的权值以及左转次数/2 的值，问蚂蚁走出的路径围出的封闭图形，权值之和最大可能是多少。

输入输出格式

输入格式：

在输入文件ant.in 中，第一行三个数n,m,k。意义如题目描述。

接下来一个n 行m 列的整数矩阵，表示棋盘。

输出格式：

一个数，表示蚂蚁所走路径围出的图形可能的最大权值和。

输入输出样例

输入样例#1：

2 5 2
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1

输出样例#1：

-8

说明

【样例说明】

除了第一行的第二个和第一行的第四个都要围起来才至少合法。

【数据规模与约定】

10%的数据所有格子中权值均非负

另20%的数据n=2

另30%的数据k=0

100%的数据1≤n≤100,1≤m≤100,0≤k≤10 保证存在合法路径，数据有梯度，格子中每个元素的值绝对值不超过 10000

题解：

首先需要看明白题，什么左转右转的

自己举几个例子就可以知道，围成的图形大概长这样：

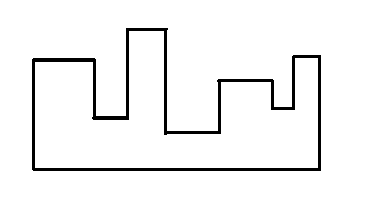
凹进去几个，就是k（比如上图k=3）

然后，其实挺明显能看出来是dp

但怎么dp是个问题！想了好久好久

一开始我是将围成的图形拆成k*2+1个矩形来想，但后来发现可以一列一列考虑

dp[i][j][h][l]表示当前起点在第i行，考虑到第j列，当前高度为h（指的是顶上那个点的行数），还可或起或伏l次（包括本次的）

dp[i][j][h][l]=max(dp[i][j+1][h][l],dp[i][j+1][h'][l-1])

前者是第j+1列与当前列高度相同（说白了在一个矩形中），后者h'就是第j+1列应比这列的高还是矮（取决于l的奇偶）

发现h'如果一个一个枚举好慢啊，那就开两个数组记录一下好了

写题时细节很多，感觉整个人都不好了……不可思议的是居然过了，还是很开心的

注意：提交的第一次只有60分，剩下的MLE了……所以说下次要注意数组大小！！！

代码：

 #include<cstdio>
 #include<iostream>
 #define INF 100000000
 using namespace std;

 const int MAXN = ;
 int dp[MAXN][MAXN][MAXN][];
 int big[MAXN][MAXN][],sml[MAXN][MAXN][];
 int a[MAXN][MAXN],sum[MAXN][MAXN];
 int n,m,k;

 int num(int y,int x0,int x){
     return sum[x][y]-sum[x][y-]-sum[x0-][y]+sum[x0-][y-];
 }

 int main()
 {
     int i,j,w,h,l,s;
     scanf("%d%d%d",&n,&m,&k);
     w=*k+;
     for(i=;i<=n;i++) sum[i][]=;
     for(i=;i<=m;i++) sum[][i]=;
     for(i=;i<=n;i++)
         for(j=;j<=m;j++){
             scanf("%d",&a[i][j]);
             sum[i][j]=sum[i-][j]+sum[i][j-]-sum[i-][j-]+a[i][j];
         }

     for(i=;i<=n;i++)
         for(j=;j<=m;j++)
             for(h=;h<=n+;h++)
                 for(l=;l<=w;l++)
                     dp[i][j][h][l]=-INF;

     for(i=;i<=n;i++){
         for(j=;j<=m;j++)
             for(h=;h<=n+;h++)
                 for(l=;l<=w;l++) big[j][h][l]=sml[j][h][l]=-INF;
         for(j=m;j>=;j--){
             for(l=;l<=(m-j+) && l<=w;l++){
                 for(h=;h<=i;h++){
                     s=num(j,h,i);
                     if(l==) {
                         if(j==m) dp[i][j][h][l]=s;
                         else dp[i][j][h][l]=s+max(,dp[i][j+][h][l]);
                     }
                     else{
                         if(l%==)
                             dp[i][j][h][l]=max(dp[i][j+][h][l],big[j+][h+][l-])+s;
                         else
                             dp[i][j][h][l]=max(dp[i][j+][h][l],sml[j+][h-][l-])+s;
                     }
                 }
                 sml[j][][l]=dp[i][j][][l];
                 for(h=;h<=i;h++) sml[j][h][l]=max(sml[j][h-][l],dp[i][j][h][l]);
                 big[j][i][l]=dp[i][j][i][l];
                 for(h=i-;h>=;h--) big[j][h][l]=max(big[j][h+][l],dp[i][j][h][l]);
             }
         }
     }

     int ans=-INF;
     for(i=;i<=n;i++)
         for(j=;j+w-<=m;j++)
             for(h=;h<=i;h++) ans=max(ans,dp[i][j][h][w]);
     printf("%d\n",ans);

     return ;
 }