推荐中的多任务学习-ESMM

本文将介绍阿里发表在 SIGIR’18 的论文ESMM《Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate》。文章提出使用多任务学习解决CVR（转化率）预估时的样本选择偏差和数据稀疏问题。

• 背景

在推荐系统、在线广告等应用中，CVR预估比CTR预估更加重要，CTR预估聚焦于点击率预估，即预测用户会不会点击，但是用户点击后进行消费才是最终目标。传统的CVR预估任务通常采用类似于CTR预估的技术，然而，这种做法存在两个重大问题：1) 样本选择偏差；2) 训练数据稀疏

1.样本选择偏差

转化是在点击之后发生，传统CVR预估模型在clicked数据上训练，但是在推理时使用了整个样本空间见图。训练样本和实际数据不服从同一分布，不符合机器学习中训练数据和测试数据独立同分布的假设。直观的说，会产生转化的用户不一定都是进行了点击操作的用户，如果只使用点击后的样本来训练，会导致CVR学习产生偏置。具体的实验结果可以见原论文[1]

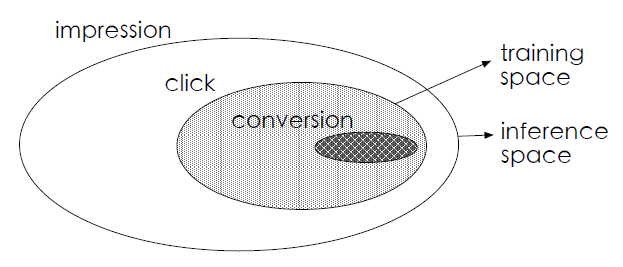
2.训练数据稀疏

训练数据稀疏问题很明显，点击样本在整个样本空间中只占了很小一部分，而转化样本更少，高度稀疏的训练数据使得模型的学习变得相当困难。

• ESMM

首先明确CTR、CVR、CTCVR。CTR表示点击率、CVR表示假设用户点击后的转化率、CTCVR表示用户点击并且成功转化。

如何解决上述问题？ESMM 引入点击率（CTR）和点击转化率（CTCVR）作为辅助任务，将CVR作为一个中间变量。它们的关系如下
\[
\underbrace{p(y=1, z=1 | x)}_{p C T C V R}=\underbrace{p(y=1 | x)}_{p C T R} \times \underbrace{p(z=1 | y=1, x)}_{p C V R}
\]
可以看出，\(pCTR\)和\(pCTCVR\)是在整个样本空间上进行学习得到的，只是label不同，\(pCVR\)是中间变量，这样就解决了样本选择偏差问题。模型架构如下

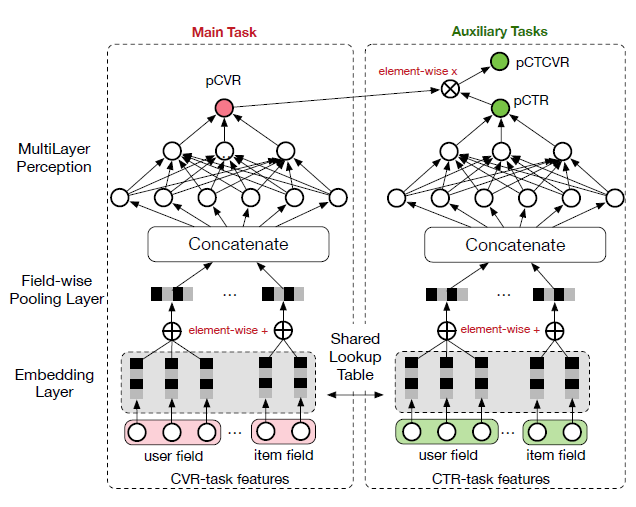
可以看出在 ESMM 中，CVR 与 CTR 任务共享Embedding 参数。这种参数共享机制使 ESMM 中的 CVR 网络可以从未点击的样本中学习，在一定程度缓解了数据稀疏性问题。

至此，两个问题已经被解决了，下面看下ESMM如何学习，模型的损失函数如下：
\[
\begin{aligned}L\left(\theta_{c v r}, \theta_{c t r}\right) &=\sum_{i=1}^{N} l\left(y_{i}, f\left(x_{i} ; \theta_{c t r}\right)\right)+\sum_{i=1}^{N} l\left(y_{i} \& z_{i}, f\left(x_{i} ; \theta_{c t r}\right) \times f\left(x_{i} ; \theta_{c v r}\right)\right)\end{aligned}
\]
第一项是CTR预估的损失，点击label为1否则为0；第二项是CTCVR预估的损失，点击且转化的label为1，否则为0。

这里还有一个问题，既然\(pCTCVR\)可以由\(pCTR\)和\(pCVR\)相乘得到，那么从理论上说，转化为除法也可以，即
\[
p(z=1 | y=1, x)=\frac{p(y=1, z=1 | x)}{p(y=1 | x)}
\]
这样可以分别训练两个模型，CTR和CVCTR，最终也可以得到CVR。论文对这种情况做了实验分析，发现实际上\(pCTR\)的值较小，会引起数值不稳定。

• discussion

1. 巧妙的引入了两个辅助任务解决CVR预估，解决了样本选择偏置问题，共享参数可以缓解数据稀疏
2. 多任务学习在其他领域已经有很多应用，但在推荐中，更应该结合具体的数据和任务设计。例如，在跨领域任务中，不同领域的环境样本是不一样的，但用户信息可能有重复，那么针对这种场景怎么设计多任务学习，样本信息的利用需要更多得考虑。

references:

[1] Xiao Ma, Liqin Zhao, Guan Huang, Zhi Wang, Zelin Hu, Xiaoqiang Zhu, and Kun Gai. 2018. Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate. SIGIR (2018).

[2] https://github.com/alibaba/x-deeplearning/wiki/%E5%85%A8%E7%A9%BA%E9%97%B4%E5%A4%9A%E4%BB%BB%E5%8A%A1%E6%A8%A1%E5%9E%8B(ESMM)