POJ 3111 二分

K Best

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 10507		Accepted: 2709
Case Time Limit: 2000MS		Special Judge

Description

Demy has n jewels. Each of her jewels has some value v_i and weight w_i.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i₁, i₂, …, i_k} as

.

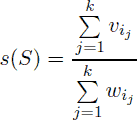Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).

The following n lines contain two integer numbers each — v_i and w_i (0 ≤ v_i ≤ 10⁶, 1 ≤ w_i ≤ 10⁶, both the sum of all v_i and the sum of all w_i do not exceed 10⁷).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

3 2
1 1
1 2
1 3

Sample Output

1 2

Source

Northeastern Europe 2005, Northern Subregion

题意：

有n个宝贝，每个宝贝有价值v和质量w要求取k个宝贝使得sum(v)/sum(w)最大，输出这k个宝贝的编号

代码：

//二分题，设最终结果是s,sum(分子)/sum(分母)=s,组成s的必然有a/b>=s和a/b<=s =>
//a-s*b>=0和a-s*b<=0，因此二分s值然后按照a-s*b从大到小排序依次取前k个看结果是否
//大于等于s
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
const double esp=0.000001;
int n,k;
double x;
struct Lu{
    int id;
    double v,w;
    bool operator < (const Lu &p)const{
        return v-x*w>p.v-x*p.w;
    }
}L[maxn];
bool solve(double m){
    x=m;
    sort(L,L+n);
    double tmp1=,tmp2=;
    for(int i=;i<k;i++){
        tmp1+=L[i].v;
        tmp2+=L[i].w;
    }
    return tmp1-m*tmp2>=0.0;
}
int main()
{
    while(scanf("%d%d",&n,&k)==){
        for(int i=;i<n;i++){
            scanf("%lf%lf",&L[i].v,&L[i].w);
            L[i].id=i;
        }
        double l=0.0,r=10000000.0;
        while(r-l>esp){
            double m=(l+r)/2.0;
            if(solve(m)){
                l=m;
            }else r=m;
        }
        for(int i=;i<k;i++)
            printf("%d%c",L[i].id+,i==k-?'\n':' ');
    }
    return ;
}