bzoj2216: [Poi2011]Lightning Conductor（分治决策单调性优化）

　　每个pi要求

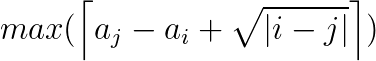
　　这个只需要正反DP（？）一次就行了，可以发现这个是有决策单调性的，用分治优化

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=,inf=1e9;
int n;
int a[maxn],f[maxn][];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
void solve(int l,int r,int L,int R,int ty)
{
    if(l>r||L>R)return;
    int mid=(l+r)>>,pos;
    double mx=0.0;
    for(int i=L;i<=R&&i<=mid;i++)
    {
        if((double)a[i]-a[mid]+sqrt(mid-i)>=mx)
        mx=(double)a[i]-a[mid]+sqrt(mid-i),pos=i;
    }
    f[mid][ty]=(int)ceil(mx);
    solve(l,mid-,L,pos,ty);solve(mid+,r,pos,R,ty);
}
int main()
{
    read(n);
    for(int i=;i<=n;i++)read(a[i]);
    solve(,n,,n,);
    reverse(a+,a++n);
    solve(,n,,n,);
    for(int i=;i<=n;i++)printf("%d\n",max(f[i][],f[n-i+][]));
}