POJ3495 Bitwise XOR of Arithmetic Progression

Time Limit: 5000MS		Memory Limit: 131072K
Total Submissions: 772		Accepted: 175

Description

Write a program that, given three positive integers x, y and z (x, y, z < 2³², x ≤ y), computes the bitwise exclusive disjunction (XOR) of the arithmetic progression x, x + z, x + 2z, …, x + kz, where k is the largest integer such that x + kz ≤ y.

Input

The input contains multiple test cases. Each test case consists of three integers x, y, z separated by single spaces on a separate line. There are neither leading or trailing blanks nor empty lines. The input ends once EOF is met.

Output

For each test case, output the value of 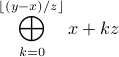 on a separate line. There should be neither leading or trailing spaces nor empty lines.

Sample Input

2 173 11

Sample Output

48

Source

POJ Founder Monthly Contest – 2008.01.31, frkstyc

 

 

数学问题 解析几何 递归

 

我可能开了假的公式支持……latex公式全都炸了，迷

upd:发现markdown编辑器的latex和这里的latex好像不太兼容，用CSDN的markdown写好公式复制过来不识别，复制到记事本里清一下文本格式再复制回来就好了

 

异或的每一位是独立的，所以可以分别计算每一位的答案。

假设现在正在处理的二进制位为 $ 2 ^ i $ ，我们需要计算

\( \left \lfloor \frac{x}{2^i} \right \rfloor + \left \lfloor \frac{x+z}{2^i} \right \rfloor + \left \lfloor \frac{x+2z}{2^i} \right \rfloor + \left \lfloor \frac{x+3z}{2^i} \right \rfloor + [f(x)] + \left \lfloor \frac{x+(n-1)z}{2^i} \right \rfloor \)

好麻烦啊，换个表示方法：

\( a=z \)

$ b=x $

$ c=2^i $

$ans=\sum_{x=0}^{n-1} \left \lfloor \frac{ax+b}{c} \right \rfloor$

$ans=\sum_{x=0}^{n-1} (\left \lfloor \frac{ax}{c} \right \rfloor +\left \lfloor \frac{b}{c} \right \rfloor +\left \lfloor \frac{(a\%c)*x+b\%c}{c} \right \rfloor) $ (1)

前两项可以提出来用等差数列求和公式算，后一项看着有点麻烦啊

把后一项画出来是这个样子：

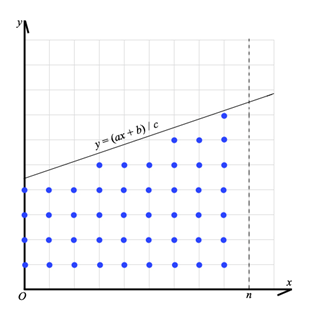
发现我们要算的是直线下面的整点的数量，即图中的蓝点数。

为了方便地计算蓝点，重建直角坐标系，像下面那样：

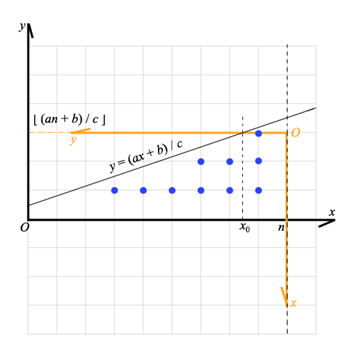
原来的直线方程是

$ \frac{(a\%c) * x + b\%c)}{c} $

现在变成了

$ \frac{cx+(an+b)\%c}{a\%c} $

(斜率取倒数，再算一下x0到n的距离作为截距)

那么

$ ans=\sum_{x=0}^{n-1} \left \lfloor \frac{ax+b}{c} \right \rfloor =\sum_{x=0}^{\lfloor (a\%c)n+(b\%c)/c +1\rfloor} \lfloor \frac{cx+(an+b)\%c}{a\%c} \rfloor $

可以发现这是一个可以递归计算的形式。

所以每次递归处理余下的部分，累加计算(1)式的前两项，算出这一位的值以后，判断二进制的这一位是奇数还是偶数，统计最终答案。

计算会爆int。

 /*by SilverN*/
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #define LL long long
 using namespace std;
 LL calc(LL a,LL b,LL c,LL n){
     if(!n)return ;
     LL tmp=(LL)a/c*n*(n-)/;
     tmp+=(LL)b/c*n;
     return tmp+calc(c,(a*n+b)%c,a%c,((a%c)*n+b%c)/c);
 }
 int main(){
     LL x,y,z;
     while(scanf("%lld%lld%lld",&x,&y,&z)!=EOF){
         LL ans=;
         for(int i=;i>=;i--){
             ans|=(calc(z,x,1ll<<i,((LL)y-x++z-)/z)&1ll)<<i;
         }
         printf("%lld\n",ans);
     }
     return ;
 }