3.1 C语言_实现AVL平衡二叉树
【序】
上节我们实现了数据结构中最简单的Vector,那么来到第三章,我们需要实现一个Set
set的特点是 内部有序且有唯一元素值;同时各种操作的期望操作时间复杂度在O(n·logn);
那么标准的C++ STL(Standard Template Library) 容器内部使用的是什么呢?
STL使用的是红黑树或者hash Tree ,由于笔者现在的水平和精力,没时间搞这个啦,于是我就
挑了一个稍微熟悉一点的数据结构:AVL 树;
github:https://github.com/KimAlittleStar/cstd
【1.介绍】
AVL 树是根据二叉查找树改进延伸过来的,我们都知道二叉查找树中只有一个规则,
那就是根节点的元素一定会大于左孩子,小于右孩子;如果是随机数,那么我们二叉查找树的高度无限
接近于 logN(完全二叉树)。但是由于其策略,在反复的插入和删除后,普通的二叉查找树将会非常
偏科(偏向右子树)如果树的高度非常大(height == N) 那么他和链表的操作时间没有什么区别,
为了避免普通二叉查找树的缺陷,因此引申出 AVL Tree -> 平衡二叉查找树;
AVL 和普通的二叉查找树只有一个规则限制:相同节点的两个孩子的高度最大相差为1,本身节点的高度
为两个孩子节点中大的那个高度加1;
【2.基础数据结构】
使用一个node 和 正常的tree 用于管理他的根和size;node 中有左孩子 右孩子和数据还有一个记录树的
高度字节u8(unsigned char),为什么我们使用u8,因为假设在满足AVL的规则要求下,坏的情况树的深度为
deep = logn *2 +1 ; 去除一个起始位0 ,后期可能会用到的错误位 -1,那么在最差的情况下 u8 类型的高度可以存储
大概多少个节点呢:
N = 2^254 (个)而我们在tree 中 size 的类型是 u32 (unsigned int)完全够用了;
参考下图:(数据结构与算法C++.pdf)
typedef unsigned int typeClass; typedef struct __SET_typeClass_node
{
typeClass data;
struct __SET_typeClass_node *left;
struct __SET_typeClass_node *right;
u8 heigh;
} SET_typeClass_node_t; typedef struct __SET_typeClass_t
{
SET_typeClass_node_t *root;
u32 size;
} SET_typeClass_t;
【3 插入】
数据的插入还是依照我们普通的二叉树进行插入,递归判断我们的数据是否小于当前节点,
小于,递归往左走,大于,大于递归往右走,等于,不操作,真正的基础情况是判断是发现当前
节点为NULL 此时申请内存存储该元素;
SET_typeClass_node_t *SET_inserttypeClass_node_t(SET_typeClass_node_t *root,
u8 (*compare)(const typeClass *a, const typeClass *b),
const typeClass *value, u32 *size)
{
if (root == NULL)
{
root = (SET_typeClass_node_t *)malloc(sizeof(SET_typeClass_node_t));
if (root == NULL)
{
// Out of space!!!
}
else
{
root->data = (*value);
root->left = root->right = NULL;
(*size)++;
}
return root;
}
else if (compare(value, &root->data))
{
root->left = SET_inserttypeClass_node_t(root->left, compare, value, size);
}
else if (compare(&root->data, value))
{
root->right = SET_inserttypeClass_node_t(root->right, compare, value, size);
}
return root;
}
普通二叉树插入
当我们在做完这一切之后,还需要做的是维护AVL的性质:左右节点高度相差最大为1;且需要
递归查询哦。于是乎我们接下来第一步要做的是什么呢?
更新我们自己的节点的高度;
root->heigh = SET_Max(SET_heighttypeClass(root->left),
SET_heighttypeClass(root->right)) +
;
更新之后节点之后我们就会发现,哎呀,有些时候(大多数时候)AVL树的规则被破坏了,那么该
就需要处理重新符合AVL树的规则;插入之后呢可能会出现四种情况,其中两两镜像,因此我们只讨论
两种;
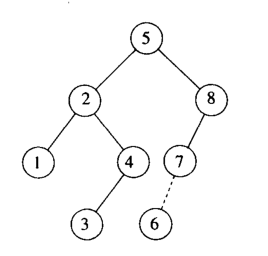
以上两种情况分别为 LL ,LR,具体判断标准为:观察高度开始不符合的节点,8号节点和 K2节点,
这里说的高度不符的节点表示:左右孩子的高度相差 >1 那么他们偏离的子节点的方向分别是
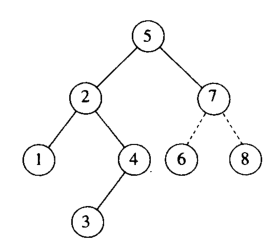
8号:Left->Left k2->Left->Right; 我们在处理LL情况的时候,只需要将7号变成5号的右孩子;
8号变成7号的右孩子即可,相当于6~7~8号顺时针旋转了一下,我们把这个定义为 ”左单旋“,旋转后
变成如下图:
相对应的也有 ”右单旋“咯。大家自己推导啦;
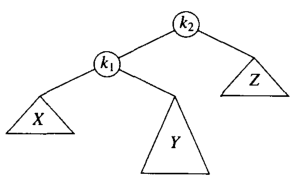
接下来看我们的LR情况,如果仅仅对K2执行一次左单旋,那么结果是:
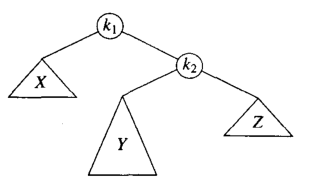
但是这样依旧没有满足 AVL 树的性质;K2的高度会比 X大超过1;此时我们需要引进一个k1的右节点进行双旋转;
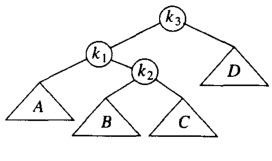
我们首先把 K1 k2 B 进行一次右单旋;得到
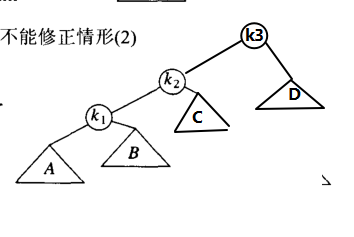
然后我们在将C~k2~k3进行一次左旋:
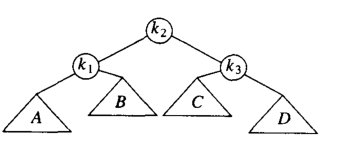
相对应的我们也会有 RL的情况,镜像情况我们就不赘述咯;
下面代码是单旋、双旋的实现:
SET_typeClass_node_t *SET_doubleRotateLefttypeClass(SET_typeClass_node_t *s)
{
s->left = SET_singleRotateRighttypeClass(s->left);
return SET_singleRotateLefttypeClass(s);
}
SET_typeClass_node_t *SET_doubleRotateRighttypeClass(SET_typeClass_node_t *s)
{
s->right = SET_singleRotateLefttypeClass(s->right);
return SET_singleRotateRighttypeClass(s);
} SET_typeClass_node_t *SET_singleRotateLefttypeClass(SET_typeClass_node_t *s)
{
SET_typeClass_node_t *s1;
s1 = s->left;
s->left = s1->right;
s1->right = s; s->heigh = SET_Max(
SET_heighttypeClass(s->left),
SET_heighttypeClass(s->right)) +
;
s1->heigh = SET_Max(
SET_heighttypeClass(s1->left),
s->heigh) +
;
return s1;
} SET_typeClass_node_t *SET_singleRotateRighttypeClass(SET_typeClass_node_t *s)
{
SET_typeClass_node_t *s1;
s1 = s->right;
s->right = s1->left;
s1->left = s; s->heigh = SET_Max(
SET_heighttypeClass(s->left),
SET_heighttypeClass(s->right)) +
;
s1->heigh = SET_Max(
SET_heighttypeClass(s1->right),
s->heigh) +
;
return s1;
}
综合以上,我们最后insert的代码就成了:
SET_typeClass_node_t *SET_inserttypeClass_node_t(SET_typeClass_node_t *root,
u8 (*compare)(const typeClass *a, const typeClass *b),
const typeClass *value, u32 *size)
{
if (root == NULL)
{
root = (SET_typeClass_node_t *)malloc(sizeof(SET_typeClass_node_t));
if (root == NULL)
{
// Out of space!!!
}
else
{
root->data = (*value);
root->left = root->right = NULL;
root->heigh = ;
(*size)++;
}
return root;
}
else if (compare(value, &root->data))
{
root->left = SET_inserttypeClass_node_t(root->left, compare, value, size);
if (SET_heighttypeClass(root->left) - SET_heighttypeClass(root->right) == )
{
if (compare(value, &root->left->data))
root = SET_singleRotateLefttypeClass(root);
else
root = SET_doubleRotateLefttypeClass(root);
}
}
else if (compare(&root->data, value))
{
root->right = SET_inserttypeClass_node_t(root->right, compare, value, size);
if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == )
{
if (compare(&root->right->data, value))
root = SET_singleRotateRighttypeClass(root);
else
root = SET_doubleRotateRighttypeClass(root);
}
}
root->heigh = SET_Max(SET_heighttypeClass(root->left),
SET_heighttypeClass(root->right)) +
;
return root;
}
AVL inser操作
然后我们使用 tree 将其包装,并且返回是否插入成功;插入不成功有两种情况(内存空间不足和元素已存在)
u8 SET_inserttypeClass_t(SET_typeClass_t *set, const typeClass ele)
{
if (set == NULL || set->compare == NULL)
return ;
u32 cursize = set->size;
set->root = SET_inserttypeClass_node_t(set->root, set->compare, &ele, &set->size);
return (cursize < set->size);
}
AVL insert 封装
【4 删除】
删除的操作呢,比插入要更加复杂一些;但是我们依旧是从基础的二叉树删除来入手;普通的二叉树首先
递归寻找到数据,然后将数据分成两种情况:该元素有两个孩子和该元素没有两个孩子;没有两个孩子的逻辑就
很简单,判断当前左孩子是否为空,是:将元素的指针指向他的右孩子,否则指向左孩子;如果两个孩子都为NULL,
指向谁都一样;
如果是有两个孩子的呢?那么我们就将这个元素下寻找到他最小的一个子辈(可能是他的孩子、孙子、曾孙、玄孙。。。)
然后把他的子辈赋值给他,然后删除他的那个子辈;因为他的子辈一定是左孩子为NULL的;
以下为实现:
SET_typeClass_node_t *SET_removetypeClass_node_t(SET_typeClass_node_t *root,
u8 (*compare)(const typeClass *a, const typeClass *b),
void (*deleteSub)(const typeClass *ele),
const typeClass *value, u32 *size)
{
if (root == NULL)
{
// no has this value
}
else if (compare(value, &root->data))
{
root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size);
}
else if (compare(&root->data, value))
{
root->right = SET_removetypeClass_node_t(root->right, compare, deleteSub, value, size);
}
else
{
/*real delete option*/
if (root->right != NULL && root->left != NULL)
{
/* has two child */
SET_typeClass_node_t *temp = root;
while (temp->left != NULL)
{
temp = temp->left;
}
if (deleteSub != NULL)
deleteSub(&root->data);
root->data = temp->data; /* deleteSub == NULL because this min not to free ,just become root->data; */
root->left = SET_removetypeClass_node_t(root->left, compare, NULL, &root->data, size);
}
else
{
/* has only child or no child */
SET_typeClass_node_t *t = (root->right == NULL) ? (root->left) : (root->right);
if (deleteSub != NULL)
deleteSub(&root->data);
free(root);
(*size)--;
root = t;
}
} return root;
}
普通二叉树remove节点
删除完节点之后,我们依旧需要考虑的问题是平衡的问题;删除会出现什么问题呢?我们上述的删除到最后
一定以删除一个在末梢的节点(孩子最多只有一个),因此我们只需要考虑此情况即可;
我们可以换一个思路,其实删除带来的影响就是在树的另一边插入了一个值;那么相对应的,那边高度高了我
就往哪边旋转就好了;只不过我们判断的时候如果是删除左边,那么我们就要判断当前是不是右边高度-左边高度 > 2 就好了。
嗯~很简单是不是?
不不不,在insert中我们判断是否需要使用双旋转的依据是:
因为在插入时,如果出现的不平衡,那么假设插入的值比当前root的右孩子要大,那么就会插入在右孩子的左边;
就会出现下图所示 (插入了 14 )此时需要双旋转,是因为k1的右孩子高度高且右孩子的左侧比右侧要高;这句话有
点绕口,我们分成两步,
第一步:k1节点破坏了AVL树的规则且需要旋转的是右边;
第二步:在k1的右孩子k3上,虽然没有违法AVL的规则,但是他的左孩子高度要比右孩子高度高;这就是我们所说
的RL情况,
所以需要双旋;
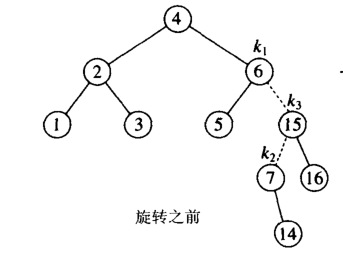
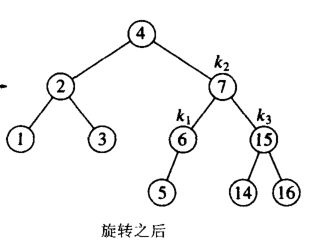
那么在删除是,也应遵循此规则,也就是说删除的时候我们就不要比较 删除值的大小啦,因为删除完值之后,
相当于我们需要知道另一侧的情况是不是需要双旋,这个时候怎么办呢?我们就依照上述一二步的原理,判断如果
左边高度高高于右边高度 >1 了,那么我就看左边孩子的两个孩子的高度是不是右边 > 左边,如果是->双旋转,如果
不是,单旋转;由于有两个孩子的节点到最后也会是删除一个叶子节点,故不需要考虑;
以下是remove判断是否需要双旋转的代码:
if (compare(value, &root->data))
{
root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size);
if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == )
{
if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left))
root = SET_singleRotateRighttypeClass(root);
else
root = SET_doubleRotateRighttypeClass(root);
}
}
remove是否需要双旋转
需要我们注意的是在删除有两个孩子的节点的时候,虽然我们是删除,但是我实际上还是调用的递归,一次我们还
是需要判断一次平衡规则;
最后remove的代码如下:
SET_typeClass_node_t *SET_removetypeClass_node_t(SET_typeClass_node_t *root,
u8 (*compare)(const typeClass *a, const typeClass *b),
void (*deleteSub)(const typeClass *ele),
const typeClass *value, u32 *size)
{
if (root == NULL)
{
// no has this value
}
else if (compare(value, &root->data))
{
root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size);
if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == )
{
if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left))
root = SET_singleRotateRighttypeClass(root);
else
root = SET_doubleRotateRighttypeClass(root);
}
}
else if (compare(&root->data, value))
{
root->right = SET_removetypeClass_node_t(root->right, compare, deleteSub, value, size);
if (SET_heighttypeClass(root->left) - SET_heighttypeClass(root->right) == )
{
if (SET_heighttypeClass(root->left->left) > SET_heighttypeClass(root->left->right))
root = SET_singleRotateLefttypeClass(root);
else
root = SET_doubleRotateLefttypeClass(root);
}
}
else
{
/*real delete option*/
if (root->right != NULL && root->left != NULL)
{
/* has two child */
SET_typeClass_node_t *temp = root;
while (temp->left != NULL)
{
temp = temp->left;
}
if (deleteSub != NULL)
deleteSub(&root->data);
root->data = temp->data; /* deleteSub == NULL because this min not to free ,just become root->data; */
root->left = SET_removetypeClass_node_t(root->left, compare, NULL, &root->data, size);
if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == )
{
if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left))
root = SET_singleRotateRighttypeClass(root);
else
root = SET_doubleRotateRighttypeClass(root);
}
}
else
{
/* has only child or no child */
SET_typeClass_node_t *t = (root->right == NULL) ? (root->left) : (root->right);
if (deleteSub != NULL)
deleteSub(&root->data);
free(root);
(*size)--;
root = t;
}
}
if (root != NULL)
root->heigh = SET_Max(SET_heighttypeClass(root->left),
SET_heighttypeClass(root->right)) +
;
return root;
}
AVL remove 代码
同理使用一个tree对他进行封装,同时返回是否remove成功,remove不成功只有一种可能,那就是set中不存在此元素;
u8 SET_removetypeClass_t(SET_typeClass_t *set, const typeClass ele)
{
if (set == NULL || set->compare == NULL)
return ;
u32 cursize = set->size;
set->root = SET_removetypeClass_node_t(set->root, set->compare, set->deleteSub, &ele, &set->size);
return (cursize > set->size);
}
在AVL树中最重要的就是插入和删除啦;
其他的像 delete 遍历呀,find findMax之类的太简单我就不说啦。基本上就是使用遍历或者一直往右找或往左找;
最后我考虑到上文中SET_typeClass_t是一个类型,所以所有的比较都抽象化了compare函数,还有有可能在删除的时候
需要释放SET_typeClass_t中指向的空间,所以抽象化成为函数指针deleteSub;
【结束语】
下一节就是将我们今天所实现的这些函数变成宏,完成 STL 数据容器 SET
目录
1.引言
3.2 C语言_实现数据容器set(基础版)
4 C语言_实现简单基础的map
参考资料 : 数据结构与算法C++实现.pdf;
3.1 C语言_实现AVL平衡二叉树的更多相关文章
- 2.2 C语言_实现数据容器vector(排序功能)
上一节我们说到我们己经实现了一般Vector可以做到的自动扩充,告诉随机存取,那么现在我们需要完成vector的一个排序的功能. 排序算法我们网上一百度哇~~!很常见的就有8大排序算法: 1.选择排序 ...
- 怎样让Oracle支持中文? 语言_地域.字符集
暂时不涉及数据库业务,但是今天入库的时候中文入库报错,考虑可能是字体不支持,留待备用. 来源:Linux社区 作者:robertkun 语言_地域.字符集SIMPLIFIED CHINESE_CHI ...
- 数据结构中很常见的各种树(BST二叉搜索树、AVL平衡二叉树、RBT红黑树、B-树、B+树、B*树)
数据结构中常见的树(BST二叉搜索树.AVL平衡二叉树.RBT红黑树.B-树.B+树.B*树) 二叉排序树.平衡树.红黑树 红黑树----第四篇:一步一图一代码,一定要让你真正彻底明白红黑树 --- ...
- c语言_常见图片格式判断
c语言_常见图片格式判断 我想尽各种思路.今天,终于把图片判断搞定了. 在此,我写一下我的思路.希望对那些不想看代码的朋友们有帮助. 常风的的图片格式有:bmp,png,jpg,gif等图片格式. 我 ...
- BZOJ_1212_[HNOI2004]L语言_哈希
BZOJ_1212_[HNOI2004]L语言_哈希 Description 标点符号的出现晚于文字的出现,所以以前的语言都是没有标点的.现在你要处理的就是一段没有标点的文章. 一段文章T是由若干小写 ...
- 选择排序_C语言_数组
选择排序_C语言_数组 #include <stdio.h> void select_sort(int *); int main(int argc, const char * argv[] ...
- 插入排序_C语言_数组
插入排序_C语言_数组 #include <stdio.h> void insertSort(int *); int main(int argc, const char * argv[]) ...
- 快速排序_C语言_数组
快速排序_C语言_数组 #include <stdio.h> void quickSort(int *, int, int); int searchPos(int *, int, int) ...
- 冒泡排序_C语言_数组
冒泡排序_C语言_数组 #include <stdio.h> //冒泡排序 小->大 void sort(int * pArray, int len); int main(int a ...
随机推荐
- Java连载33-对象的创建和使用、内存分析
一.创建一个学生类 每个学生都有学号信息,但是每一个学生的学号都是不同的,所以要访问这个学号必须先创建对象,通过对象去访问学号信息,学号信息不能直接通过“类”去访问,所以这种成员变量又被称为“实例变量 ...
- vue中事件修饰符详解(stop, prevent, self, once, capture, passive)
==.stop== 是阻止冒泡行为,不让当前元素的事件继续往外触发,如阻止点击div内部事件,触发div事件 ==.prevent== 是阻止事件本身行为,如阻止超链接的点击跳转,form表单的点击提 ...
- 为elastic的索引做快照并恢复快照到新集群
1. 为指定的所有做快照 curl -XPUT "192.168.1.1:9200/_snapshot/my_backup/testindex_20170803?wait_for_compl ...
- 这个注册的 IP 网络都不通了,Eureka 注册中心竟然无法踢掉它!
本文导读: 微服务技术架构选型介绍 k8s 容器化部署架构方案 Eureka 注册中心问题场景 问题解决手段及原理剖析 阅读本文建议先了解: 注册中心基本原理 K8s(Kuberneters)基本概念 ...
- Android Studio [水平布局LinearLayout]
<?xml version="1.0" encoding="utf-8"?> <LinearLayout xmlns:android=&quo ...
- java 队列和栈相互实现
一.队列实现栈 public class queue2stack { public static void main(String[] args) { QS qs = new QS(); qs.pus ...
- WebGL简易教程(九):综合实例:地形的绘制
目录 1. 概述 2. 实例 2.1. TerrainViewer.html 2.2. TerrainViewer.js 3. 结果 4. 参考 1. 概述 在上一篇教程<WebGL简易教程(八 ...
- redis查找大key
redis中查找出比较大的key 下面直接上代码 (请在测试机上测试) #!/usr/bin/env python import sys import redis def check_big_key( ...
- Java 学习笔记之 线程Yield
线程Yield: yield()方法的作用是放弃当前的CPU资源,将它让给其他的任务去占用CPU执行时间,但放弃的时间不确定,有可能刚刚放弃,马上又获得CPU时间片. public class Yie ...
- 通过搭建MySQL掌握k8s(Kubernetes)重要概念(下):参数配置
本文通过搭建MySQL环境来了解k8s的重要概念,包括持久卷,网络和参数配置.这是下篇,专门讲解参数配置.如果你有些地方不能完全看明白,请先看上篇"通过搭建MySQL掌握k8s(Kubern ...
