PCA(主成分分析)原理,步骤详解以及应用

主成分分析(PCA, Principal Component Analysis)

一个非监督的机器学习算法
主要用于数据的降维处理
通过降维,可以发现更便于人类理解的特征
其他应用:数据可视化,去噪等

主成分分析是尽可能地忠实再现原始重要信息的数据降维方法

原理推导:

如图,有一个二维的数据集,其特征分布于特征1和2两个方向

现在希望对数据进行降维处理,将数据压缩到一维,直观的我们可以想到将特征一或者特征二舍弃一个,可以得到这样的结果

　　　　　　　　------- : 舍弃特征1之后

　　　　　　　　------- : 舍弃特征2之后

可以看出,舍弃特征2保留特征1是一个较好的降维方案,此时点和点之间距离较大,拥有更高的可区分度

此时我们要想,肯定会有比这更好的方案,毕竟这太简单了

我们想象一下,能够找到这样的一条斜线w,将数据降维到w上(映射到w上)之后,能最好的保留原来的分布特征,且这些点分布在了一个轴上(斜线w)后点和点之间的距离也比之前的两种方案更加的大,此时的区分度也更加明显

思考:

如何找到让这个样本降维后间距最大的轴?
如何定义样本间距?

在统计学中,有一个直接的指标可以表示样本间的间距,那就是方差(Variance)

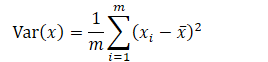
这样回过头来看思考1,问题就变成了:

找到一个轴,使得样本空间的所有点映射到这个轴之后,方差最大

求解这个轴的过程

将样例的均值归为0(demean)

　　将全部样本都减去样本的均值,可以将样本转化为这种:

　　经过demean后,在各个维度均值均为0,我们可以推出:

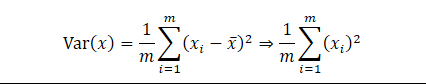
　　方便我们进行计算

我们想要求w轴的方向(w₁,w₂),使得 Var(X_project) 最大,X_project是映射到w轴之后的X的坐标

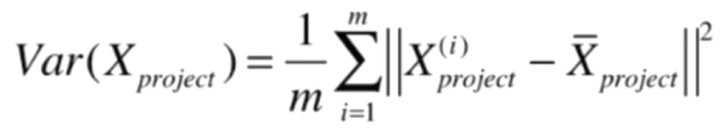
因为我们已经进行了demean操作,均值为0,所以此时

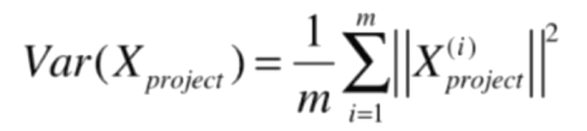
而 ||X_project⁽ⁱ⁾||² 的实际长度就是下图中蓝色向量的长度

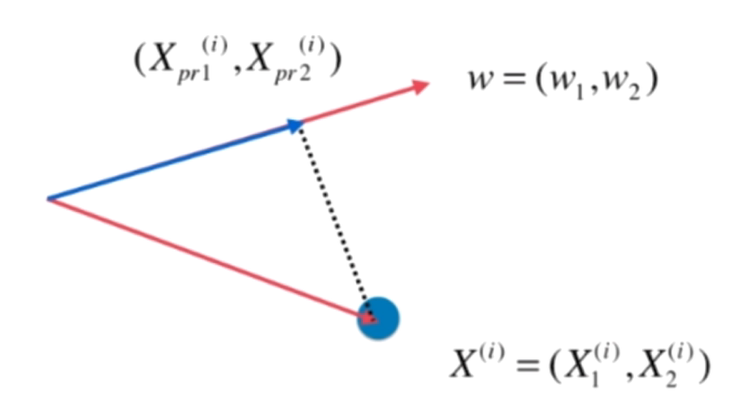
实际上,求把一个向量映射到另一个向量上的对应映射的长度,就是线性代数中点乘的操作

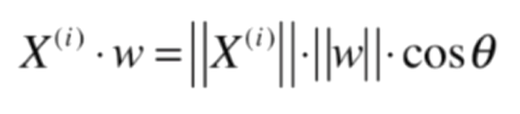
此时w是一个方向向量,||w|| = 1,所以可以化简成:

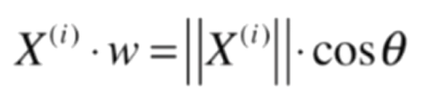
且因为前面已经推知

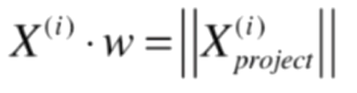
通过替换,我们就得到了:

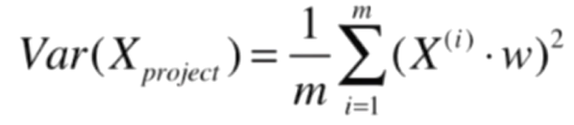
而我们的目标,就是求w,使得Var(X_project) 最大

对公式进行拆分

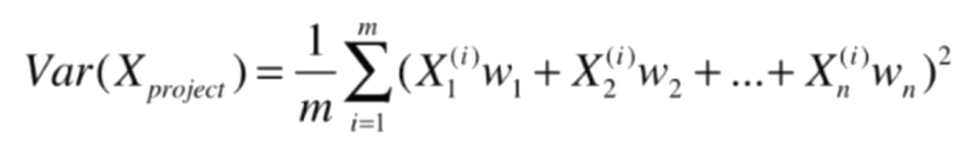
再化简:

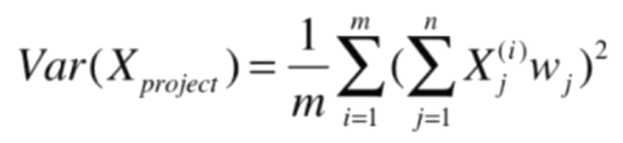
至此,我们的主成分分析法就化简成了一个目标函数最优化问题,因为是求最大值,可以使用梯度上升法解决

使用梯度上升法求解PCA

目标: 求w,使得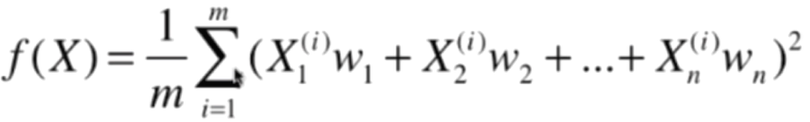最大

f(X)的梯度

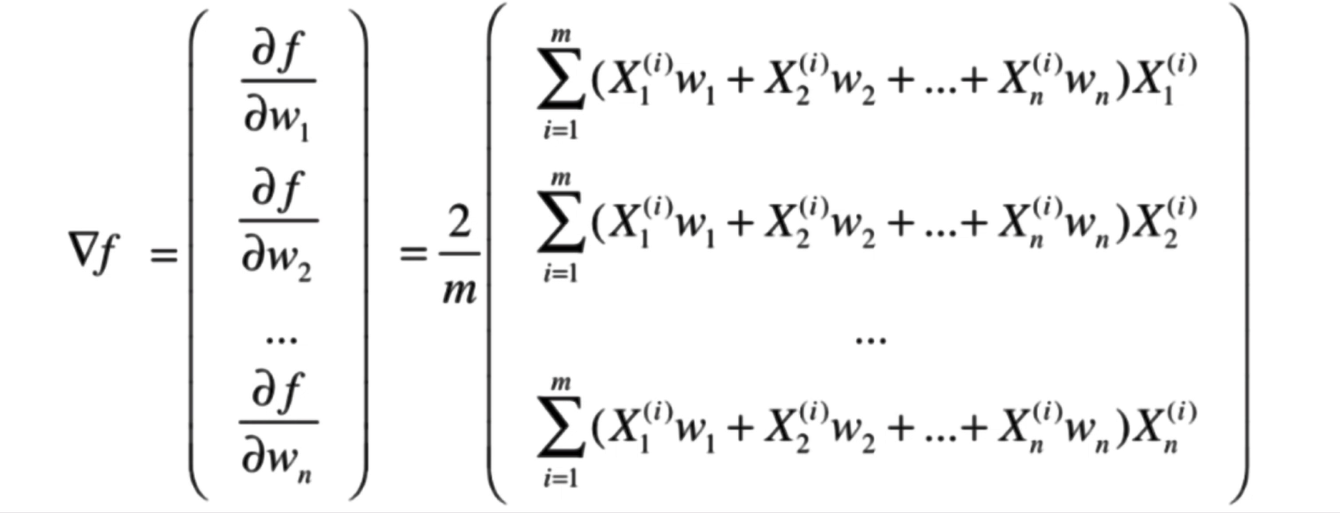
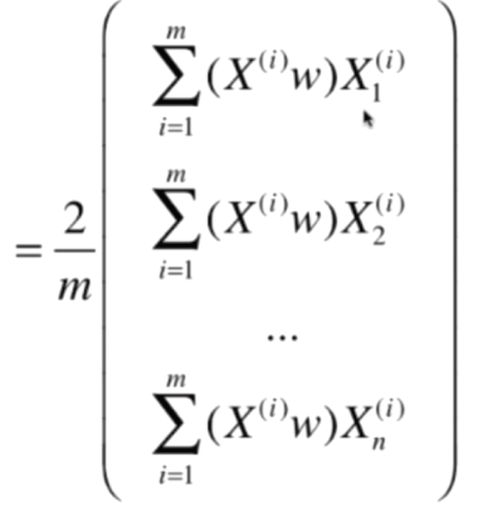
此时再观察,可以将式子展开能够得到这样的结果:

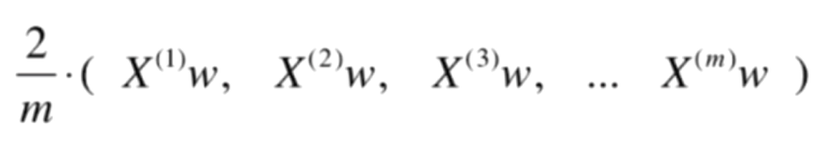
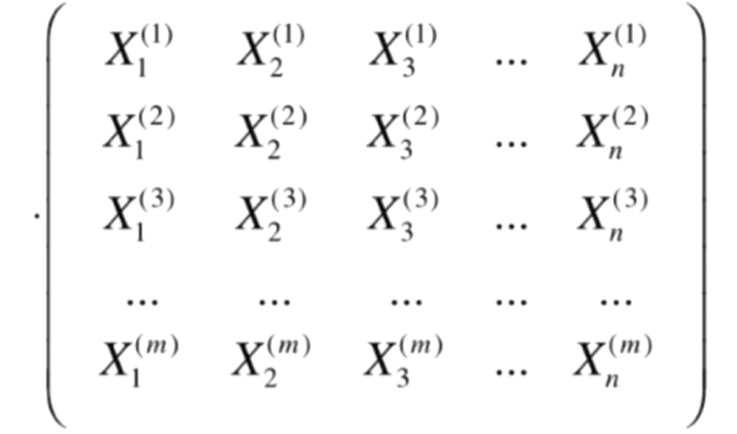
再化简,可得:

　　原式 =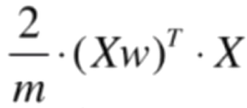

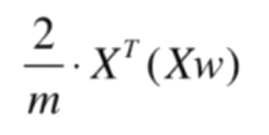
最后就得出结论:

那么,求出第一个主成分之后,如何求出下一个主成分呢?

数据进行改变,将数据在第一主成分上的分量去掉,如图

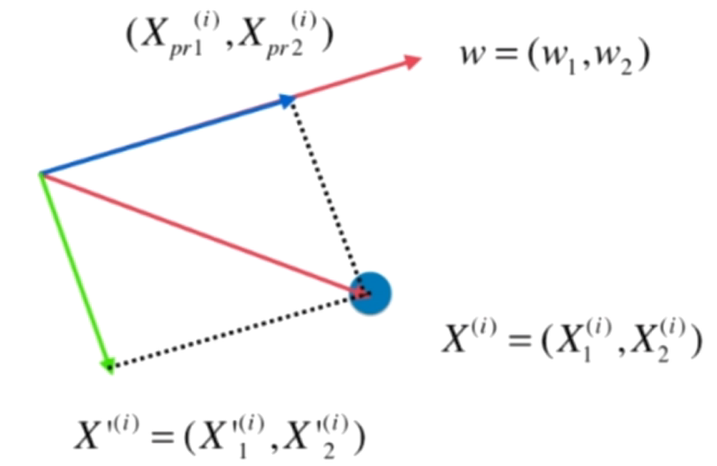
Xpr⁽ⁱ⁾ 是第一主成分,原数据去掉第一主成分之后可以得到

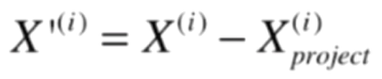
再在 X'⁽ⁱ⁾ 上求第一主成分即可求出原数据的第二主成分,以此类推..

代码实现

 import numpy as np

 import matplotlib.pyplot as plt

 # 生成测试数据

 X = np.empty((100, 2))

 X[:, 0] = np.random.uniform(0., 100., size=100)

 X[:, 1] = 0.75 * X[:, 0]+ 3. + np.random.normal(0, 10., size=100)

 #  均值归零方法

 def demean(X):

     return X - np.mean(X, axis=0)

 X_demean = demean(X)

 #  梯度上升法

 def f(w, X):

     return np.sum((X.dot(w)**2)) / len(X)

 def df(w, X):

     return X.T.dot(X.dot(w)) * 2. / len(X)

 #  将w转化为单位向量,方便计算

 def direction(w):

     return w / np.linalg.norm(w)

 #求第一主成分

 def first_component(X, initial_w, eta, n_iters = 1e4, epsilon = 1e-8):

     w = direction(initial_w)

     cur_iter = 0

     while cur_iter < n_iters:

         gradient = df(w, X)

         last_w = w

         w = w + eta * gradient

         w = direction(w)  # 每次求一个单位方向

         if abs(f(w, X) - f(last_w, X)) < epsilon:

             break

         cur_iter += 1

     return w

 initial_w = np.random.random(X.shape[1]) # 不能从零开始

 eta = 0.01

 def first_n_component(n, X, eta=0.01, n_iters = 1e4, espilon = 1e-8):

     X_pca = X.copy()

     X_pca = demean(X_pca)

     res = []

     for i in range(n):

         initial_w = np.random.random(X_pca.shape[1])

         w = first_component(X_pca, initial_w, eta)

         res.append(w)

         X_pca = X_pca - X_pca.dot(w).reshape(-1, 1)

         X_pca = X_pca * w

     return res

 # 注意 不能使用StandardScaler标准化数据 这样会打掉样本间的方差 求不出想要的结果

 res = first_n_component(2, X)