sierpinski垫片(3D)[误]

今天是因为可以用py而高兴的一天。

昨天老板淡淡地回了一句，sierpinski地毯画得挺好的。

我思考了五秒钟之后，想起来作业其实是sierpinski垫片。

 

 

三角垫片比地毯难做多了。

因为你用的像素点，其实是矩形，你可以把像素点当矩形用。

三角形，随机算法可以，你要我用传统算法来解那个三角垫片，我只想给你以窝jio。除非你给我一个三角网格。

所以在jpg里玩，没tai意nan思le。你说你解完，反不反走样。。。是吧。。。反走样很蠢，走样了很丑。

所以，我决定用.ply来存这玩意。。。话说，既然这么用，干脆搞个大新闻好了。

不然你说，在三维空间里存了一堆平面上的三角，哈哈哈哈哈次藕爆了。

可是道理我都懂，为啥底是矩形呢。。。[图片来自百度，侵删]

所以，我们要整个更好看的哈哈哈哈哈。

算法逻辑：

每个四面体生成四个小四面体并多出六个顶点。

最终是要输出三角面片，可是在这之前我一直是体在拆解啊。

所以我中间过程存储体的信息，最后一步拆成四个面就好了。

每一轮，四面体信息矩阵扩大四倍。

　　每个四面体拆解都会成四个小四面体存入对应四行。

　　顶点通过取中点取到六个，信息补上6个。

import numpy as np
import cv2

def beiup(x1,x2,x3,x4):
    x=np.zeros((6,3),dtype=float)
    for j in range(3):
        x[0][j]=(x1[j]+x2[j])/2
        x[1][j]=(x2[j]+x3[j])/2
        x[2][j]=(x3[j]+x1[j])/2
        x[3][j]=(x4[j]+x1[j])/2
        x[4][j]=(x4[j]+x2[j])/2
        x[5][j]=(x4[j]+x3[j])/2
    return x
def yeiup(yei,jsq):
    new=np.zeros((4,4),dtype=int)
    new[0][0]=yei[0]
    new[0][1]=jsq
    new[0][2]=jsq+2
    new[0][3]=jsq+3
    new[1][0]=jsq
    new[1][1]=yei[1]
    new[1][2]=jsq+1
    new[1][3]=jsq+4
    new[2][0]=jsq+2
    new[2][1]=jsq+1
    new[2][2]=yei[2]
    new[2][3]=jsq+5
    new[3][0]=jsq+3
    new[3][1]=jsq+4
    new[3][2]=jsq+5
    new[3][3]=yei[3]
    jsq+=6
    return new,jsq
def feiwrite(yeimat,times):
    k=4**times
    feimat=np.zeros((k*4,3),dtype=int)
    for i in range(k):
        feimat[i*4+0][0]=yeimat[i][0]
        feimat[i*4+0][1]=yeimat[i][2]
        feimat[i*4+0][2]=yeimat[i][1]
        feimat[i*4+1][0]=yeimat[i][0]
        feimat[i*4+1][1]=yeimat[i][1]
        feimat[i*4+1][2]=yeimat[i][3]
        feimat[i*4+2][0]=yeimat[i][0]
        feimat[i*4+2][1]=yeimat[i][3]
        feimat[i*4+2][2]=yeimat[i][2]
        feimat[i*4+3][0]=yeimat[i][1]
        feimat[i*4+3][1]=yeimat[i][2]
        feimat[i*4+3][2]=yeimat[i][3]
    return feimat        

def plywrite(fname,beimat,feimat,potnumber,trinumber):
    potpiplist=np.zeros((3),dtype=float)
    tripiplist=np.zeros((3),dtype=int)
    fply = open(fname,'w')
    fply.write('ply\n')
    fply.write('format ascii 1.0\n')
    fply.write('comment VCGLIB generated\n')
    fply.write('element vertex '+str(potnumber)+'\n')
    fply.write('property float x\n')
    fply.write('property float y\n')
    fply.write('property float z\n')
    fply.write('element face '+str(trinumber)+'\n')
    fply.write('property list uchar int vertex_indices\n')
    fply.write('end_header\n')
    for i in range(potnumber):
        potpiplist[0]=beimat[i][0]
        potpiplist[1]=beimat[i][1]
        potpiplist[2]=beimat[i][2]
        fply.write('%0.4f %0.4f %0.4f\n' %(potpiplist[0],potpiplist[1],potpiplist[2]))
    for i in range(trinumber):
        tripiplist[0]=feimat[i][0]
        tripiplist[1]=feimat[i][1]
        tripiplist[2]=feimat[i][2]
        fply.write('%d %d %d %d\n' %(3,tripiplist[0],tripiplist[1],tripiplist[2]))
    fply.close()
    return fname

　　

解释一下变量名。

我最近在捣腾一个TPS的大项目。

ply文件有两个主要部分

一个是点坐标信息，beimat      顶点数*3,  float

一个是面片顶点信息，feimat   面片数*3,  int 对应beimat的第i个。

以前没有四面体一说，yeimat   体数*4   ,  int

bei是我的名字，fei是我姐上的名。

口哼哼，我不管，反正项目我最后封装掉的。

beiup解决了如何拆出六个中点；

yeiup解决了如何拆出四个体；

feiwrite解决了如何从一个体拆除四个面片。

import numpy as np
import cv2
import tps
import sie

times=1
if times<4:
    beimat=np.zeros((600,3),dtype=float)
if times<6:
    beimat=np.zeros((2100,3),dtype=float)
if times<10:
    beimat=np.zeros((9000,3),dtype=float)

yeimat=np.zeros((1,4),dtype=int)
'''
0,0,0; 1,0,0; 0.5,g3/2,0 ;0.5 g3/6,g6/3)
'''
beimat[1][0]=1
beimat[2][0]=0.5
beimat[2][1]=(3**0.5)/2
beimat[3][0]=0.5
beimat[3][1]=(3**0.5)/6
beimat[3][2]=(6**0.5)/3

yeimat[0][1]=1
yeimat[0][2]=2
yeimat[0][3]=3
###end for setting

jsq=4
for k in range(times):
    yeinew=np.zeros((4**k*4,4),dtype=int)
    for n in range(4**k):
        beimat[jsq:jsq+6,:]=sie.beiup(beimat[int(yeimat[n][0])],beimat[int(yeimat[n][1])],beimat[int(yeimat[n][2])],beimat[int(yeimat[n][3])])
        [yeinew[4*n:4*n+4,:],jsq]=sie.yeiup(yeimat[n],jsq)
    yeimat=yeinew

feimat=sie.feiwrite(yeimat,times)

fname=str("sie"+str(int(times))+".ply")
print(jsq)

fname=sie.plywrite(fname,beimat[0:jsq,:],feimat,jsq,4**times*4)

　　

主程序有三部分：

决定beimat的大小

初始化第一个四面体（顶点坐标+编号）

主循环体+输出。

你说我不能算出来beimat应该有多大么？

毕竟是学树学的，这如果算不出来实在是无能。。。问题是，我有必要算么？

如果你要算的话，就是x=x*4-6的一个递归数列。。。可以，但没必要。

我jsq最后会告诉我有多少个坐标点的。。。我只要，一开始不把beimat设太小就好了。

这里四个是1-4次迭代；下方几个都是5/6次迭代。

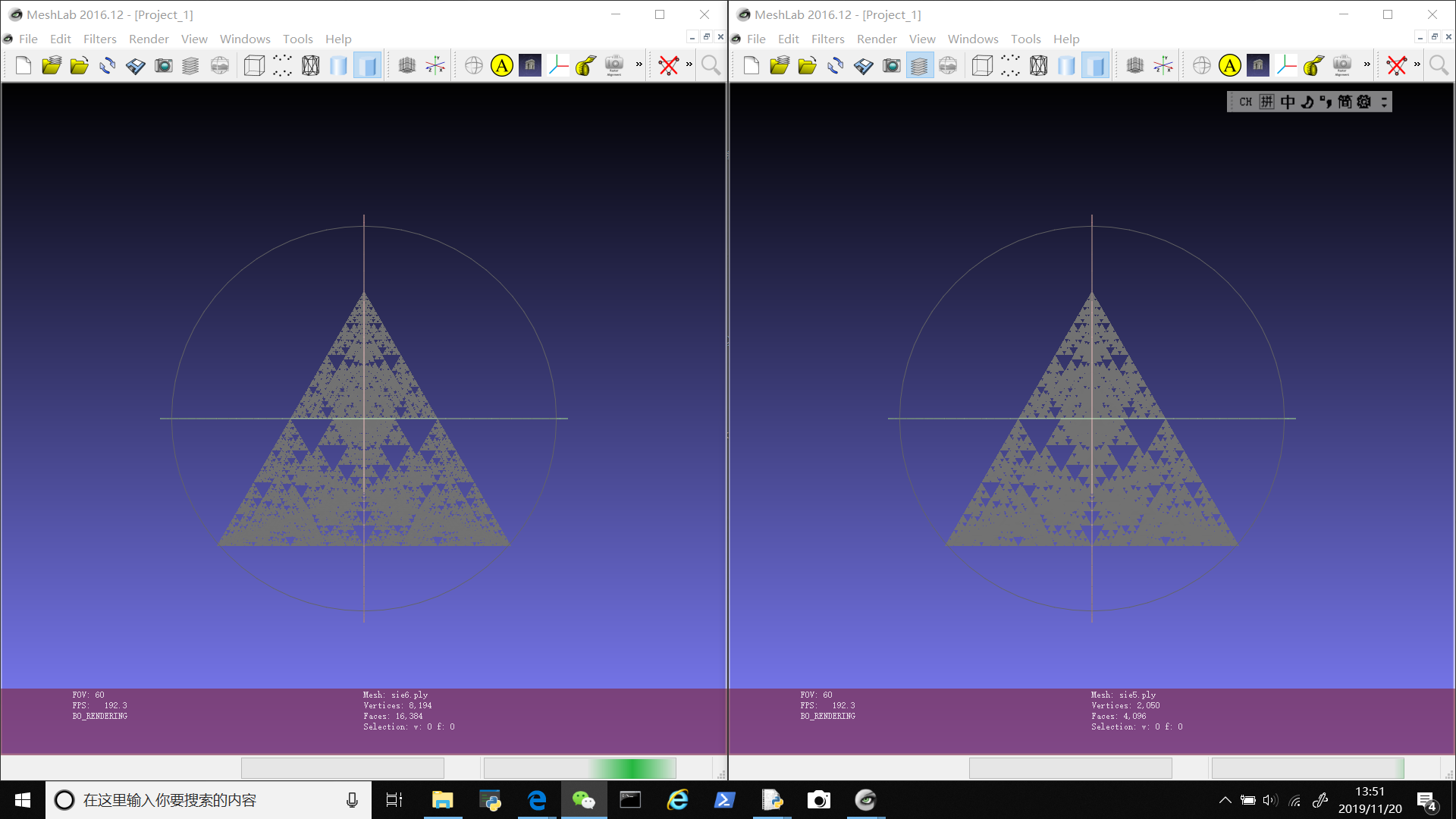
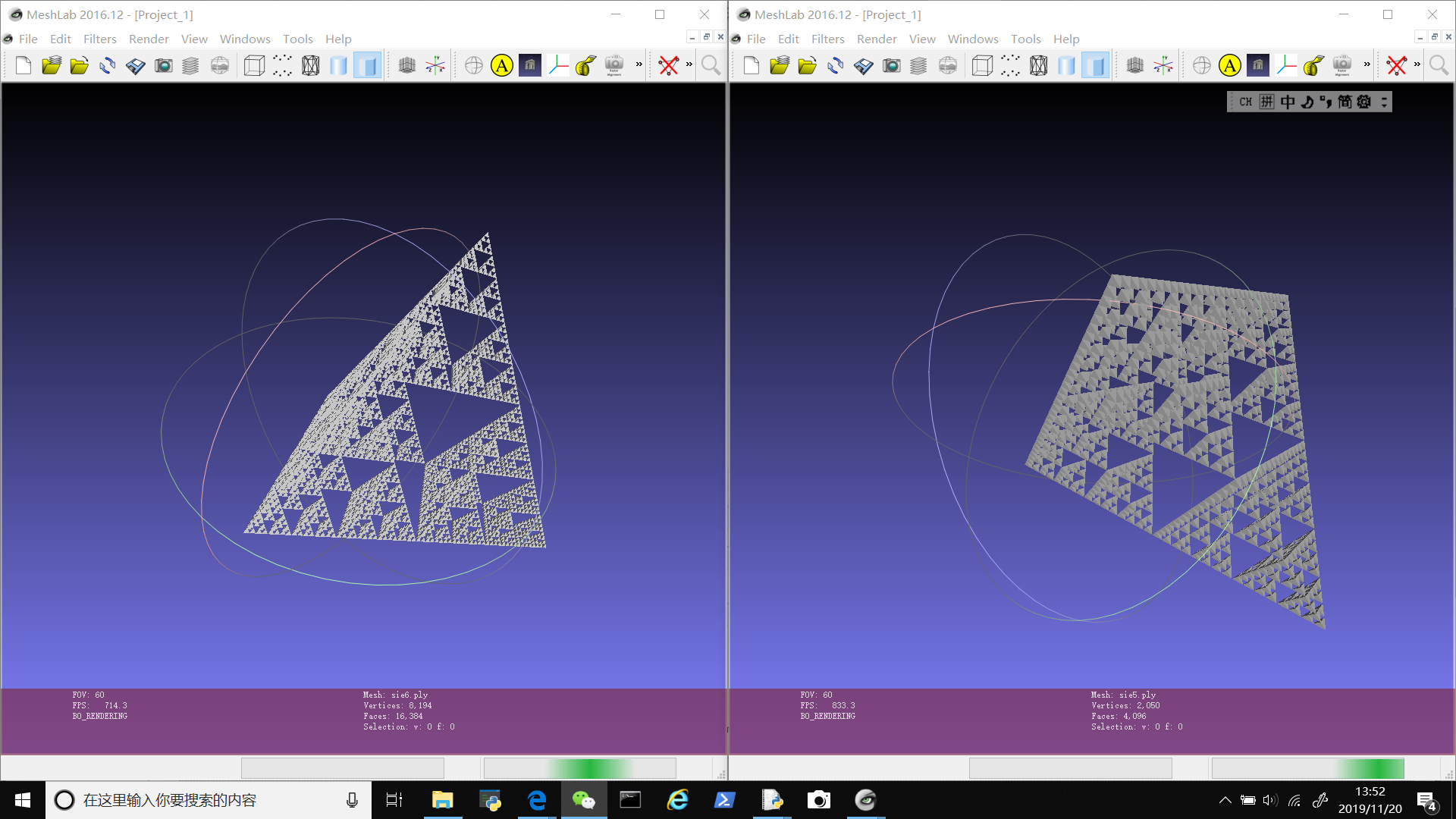
嘿嘿嘿！py万岁！