从零开始openGL——三、模型加载及鼠标交互实现
前言
在上篇文章中,介绍了基本图形的绘制。这篇博客中将介绍模型的加载、绘制以及鼠标交互的实现。
模型加载
模型存储
要实现模型的读取、绘制,我们首先需要知道模型是如何存储在文件中的。
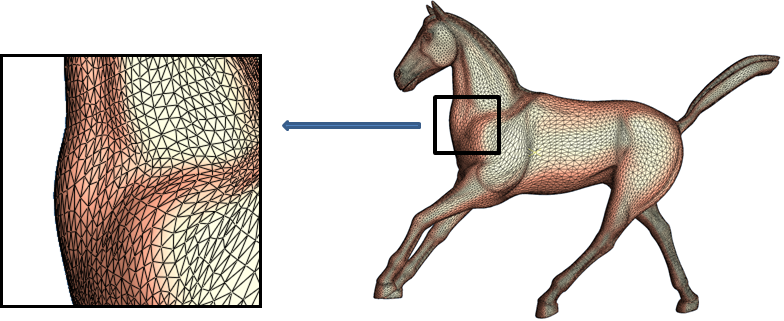
通常模型是由网格组成的,且一般为三角网格。原因为:
- 其它多边形网格可以容易地剖分为三角形
- 三点共面:保证平面性
- 可以容易地定义内外方向,进行插值等操作
可采用地数据结构包括:
- 面列表
- 存储面中顶点的三元组(v1, v2, v3)
- 优点:方便而紧凑,可表达非流行网格
- 缺点:不能有效地支持点、面之间的邻接关系查询
- 邻接矩阵
- 优点:支持顶点之间的邻接信息(VV)的高效查询、支持非流行网格
- 缺点:没有边的显示表达、不支持VF(vertex to face),VE(vertex to edge),EV(edge to vertex),FE(face to edge),EF(edge to face)的快速查询
- 半边结构等
- 纪律所有的面、边和顶点,包括几何信息、拓扑信息、附属属性,流行于大部分集合建模应用
- 优点:所有查询操作时间复杂度均为o(1),所有编辑操作时间复杂度均为o(1)
- 缺点:只能表达流行网格
- 常用半边结构实现:CGAL(http://www.cgal.org/),Open Mesh(http://www.openmesh.org/)
在这里,我使用的是面列表。
先定义头文件
#ifndef OBJ_CLASS
#define OBJ_CLASS #include <vector>
#include <cmath> struct Vector3;
Vector3 operator + (const Vector3& one, const Vector3& two);
Vector3 operator - (const Vector3& one, const Vector3& two);
Vector3 operator * (const Vector3& one, double scale);
Vector3 operator / (const Vector3& one, double scale);
Vector3 Cross(Vector3& one, Vector3& two); struct Vector3
{
double fX;
double fY;
double fZ;
Vector3(double x = 0.0, double y = 0.0, double z = 0.0) : fX(x), fY(y), fZ(z) {}
Vector3 operator +=(const Vector3& v) { return *this = *this + v; }
double Length() { return sqrt(fX * fX + fY * fY + fZ * fZ); }
void Normalize()//归一化
{
double fLen = Length();
if (fLen == 0.0f)
fLen = 1.0f;
if (fabs(fLen) > 1e-)
{
fX /= fLen;
fY /= fLen;
fZ /= fLen;
}
}
}; struct Point
{
Vector3 pos;
Vector3 normal;
}; struct Face
{
int pts[];
Vector3 normal;
}; class CObj
{
public:
CObj(void);
~CObj(void); std::vector<Point> m_pts; //顶点
std::vector<Face> m_faces;//面 public:
bool ReadObjFile(const char* pcszFileName);//读入模型文件 private:
void UnifyModel();//单位化模型
void ComputeFaceNormal(Face& f);//计算面的法线
}; #endif
然后是一些简单的运算符重载以及向量计算
#include "Obj.h"
#include <iostream>
#include <sstream>
#include <algorithm> using std::min;
using std::max; Vector3 operator + (const Vector3& one, const Vector3& two) //两个向量相加
{
return Vector3(one.fX + two.fX, one.fY + two.fY, one.fZ + two.fZ);
} Vector3 operator - (const Vector3& one, const Vector3& two) //两个向量相减
{
return Vector3(one.fX - two.fX, one.fY - two.fY, one.fZ - two.fZ);
} Vector3 operator * (const Vector3& one, double scale) //向量与数的乘操作
{
return Vector3(one.fX * scale, one.fY * scale, one.fZ * scale);
} Vector3 operator / (const Vector3& one, double scale) //向量与数的除操作
{
return one * (1.0 / scale);
} Vector3 Cross(Vector3& one, Vector3& two)
{//计算两个向量的叉积
Vector3 vCross; vCross.fX = ((one.fY * two.fZ) - (one.fZ * two.fY));
vCross.fY = ((one.fZ * two.fX) - (one.fX * two.fZ));
vCross.fZ = ((one.fX * two.fY) - (one.fY * two.fX)); return vCross;
} CObj::CObj(void)
{
} CObj::~CObj(void)
{
}
下面来讲讲模型的读取等操作
模型读取
一般在模型存储文件中会有这么几个标识符:
- v 表示顶点位置
- vt 表示顶点纹理坐标
- vn 表示顶点法向量
- f 表示一个面
打开一看,大概是这样的
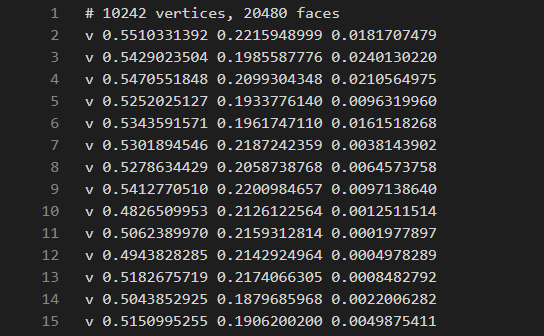
那么,就可以开始考虑如何读取并将数据存储到列表里面了,读文件还是简单的,fopen(), fgets(), feof(),剩下关键便是将字符串转成数字,c++中还是有现成的函数可以调用的,sstream头文件中的istringstream。
bool CObj::ReadObjFile(const char* pcszFileName)
{//读取模型文件 FILE* fpFile = fopen(pcszFileName, "r"); //以只读方式打开文件
if (fpFile == NULL)
{
return false;
} m_pts.clear();
m_faces.clear(); //TODO:将模型文件中的点和面数据分别存入m_pts和m_faces中
char strLine[];
Point point;
Face face;
std::string s1;
while (!feof(fpFile))
{
fgets(strLine, , fpFile);
if (strLine[] == 'v')
{
if (strLine[] == 'n')
{//vn 我使用的文件中没有vn的数据,就没有实现 }
else
{//v 点
std::istringstream sin(strLine);
sin >> s1 >> point.pos.fX >> point.pos.fY >> point.pos.fZ;
m_pts.push_back(point);
}
}
else if (strLine[] == 'f')
{// 面
std::istringstream sin(strLine);
sin >> s1 >> face.pts[] >> face.pts[] >> face.pts[];
ComputeFaceNormal(face);
m_faces.push_back(face);
}
printf("%s\n", strLine);
} fclose(fpFile); UnifyModel(); //将模型归一化 return true;
}
通过上一篇文章绘制圆环和圆柱,知道了法向量是十分重要的,因此计算每个面的法向量也是不可少的
原理很简单,叉乘即可
void CObj::ComputeFaceNormal(Face& f)
{//TODO:计算面f的法向量,并保存
f.normal = Cross(m_pts[f.pts[]-].pos - m_pts[f.pts[]-].pos, m_pts[f.pts[]-].pos - m_pts[f.pts[]-].pos);
f.normal.Normalize();
}
对于模型归一化,为何要归一化呢?想象一下,你拿手机拍照,如果拍照对象离摄像头很近,那在手机中展示出来的图像会是什么样?但是如果能不在移动相机和对象之间的距离的情况下该怎么做?把对象等比压缩!
void CObj::UnifyModel()
{//为统一显示不同尺寸的模型,将模型归一化,将模型尺寸缩放到0.0-1.0之间
//原理:找出模型的边界最大和最小值,进而找出模型的中心
//以模型的中心点为基准对模型顶点进行缩放
//TODO:添加模型归一化代码 Vector3 vec_max, vec_min(1e5, 1e5, 1e5), vec;
for (int i = ; i < m_pts.size(); i++)
{
vec_max.fX = std::max(vec_max.fX, m_pts[i].pos.fX);
vec_max.fY = std::max(vec_max.fY, m_pts[i].pos.fY);
vec_max.fZ = std::max(vec_max.fZ, m_pts[i].pos.fZ); vec_min.fX = std::min(vec_min.fX, m_pts[i].pos.fX);
vec_min.fY = std::min(vec_min.fY, m_pts[i].pos.fY);
vec_min.fZ = std::min(vec_min.fZ, m_pts[i].pos.fZ);
} vec.fX = vec_max.fX - vec_min.fX;
vec.fY = vec_max.fY - vec_min.fY;
vec.fZ = vec_max.fZ - vec_min.fZ; for (int i = ; i < m_pts.size(); i++)
{
m_pts[i].normal = m_pts[i].pos;
m_pts[i].normal.fX = (m_pts[i].normal.fX - vec_min.fX) / vec.fX - 0.5f;
m_pts[i].normal.fY = (m_pts[i].normal.fY - vec_min.fY) / vec.fY - 0.5f;
m_pts[i].normal.fZ = (m_pts[i].normal.fZ - vec_min.fZ) / vec.fZ - 0.5f;
} //m_pts.push_back(vec);
}
模型绘制
对于模型的绘制,实现起来十分容易,因为有了各个面片的信息了。
void DrawModel(CObj &model)
{//TODO: 绘制模型
for (int i = ; i < model.m_faces.size(); i++)
{
glBegin(GL_TRIANGLES);
glNormal3f(model.m_faces[i].normal.fX, model.m_faces[i].normal.fY, model.m_faces[i].normal.fZ);
glVertex3f(model.m_pts[model.m_faces[i].pts[] - ].normal.fX, model.m_pts[model.m_faces[i].pts[] - ].normal.fY, model.m_pts[model.m_faces[i].pts[] - ].normal.fZ);
glVertex3f(model.m_pts[model.m_faces[i].pts[] - ].normal.fX, model.m_pts[model.m_faces[i].pts[] - ].normal.fY, model.m_pts[model.m_faces[i].pts[] - ].normal.fZ);
glVertex3f(model.m_pts[model.m_faces[i].pts[] - ].normal.fX, model.m_pts[model.m_faces[i].pts[] - ].normal.fY, model.m_pts[model.m_faces[i].pts[] - ].normal.fZ);
glEnd();
} } if (g_draw_content == SHAPE_MODEL)
{//绘制模型
glTranslatef(g_x_offset, g_y_offset, g_z_offset);
glRotatef(g_rquad_x, 0.0f, 1.0f, 0.0f);
glRotatef(g_rquad_y, 1.0f, 0.0f, 0.0f);
glScalef(g_scale_size, g_scale_size, g_scale_size);
DrawModel(g_obj); }
运行,加载模型!
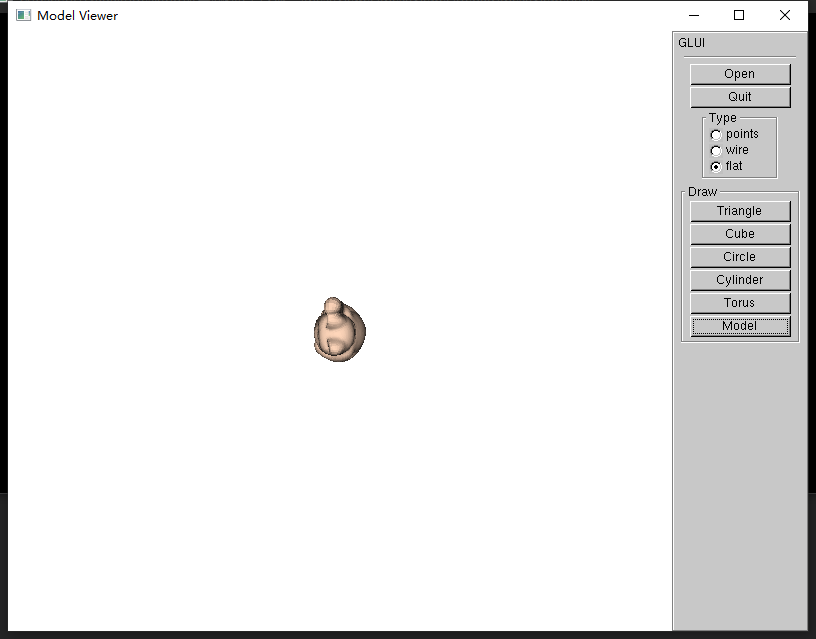
嗯,好的,它成功出来了。
等等!为啥是头对着我的,我怎么调整角度?看起来有点小,我能不能把它放大点?
下面,将介绍鼠标交互的实现。
鼠标交互
opengl中的鼠标交互还是比较好做的,首先需要的是在初始化的时候注册鼠标输出实现回调函数和鼠标移动事件的回调函数。这些在上篇文章中给的框架代码里都实现了。那剩下的就是如何实现旋转、缩放和拖动了
旋转
首先我们要注意的是,在给出的代码框架里,摄像机的lookat是这样的
gluLookAt(0.0, 0.0, 8.0, 0, 0, 0, 0, 1.0, 0);
该函数定义一个视图矩阵,并与当前矩阵相乘.
第一组eyex, eyey,eyez 相机在世界坐标的位置;第二组centerx,centery,centerz 相机镜头对准的物体在世界坐标的位置;第三组upx,upy,upz 相机向上的方向在世界坐标中的方向。
所以,这里摄像机是从z轴看下去的,那么初始看到的二维平面分为为x轴和y轴。理解了这个,旋转就很简单了。水平拖动的时候让模型绕y轴转,竖直拖动的时候让模型绕x轴转。按下左键旋转。
if (g_xform_mode == TRANSFORM_ROTATE) //旋转
{//TODO:添加鼠标移动控制模型旋转参数的代码
g_rquad_x += (x - g_press_x) * 0.5f;
g_rquad_y += (y - g_press_y) * 0.5f;
g_press_x = x;
g_press_y = y;
}
平移
平移的实现十分简单,计算鼠标移动的距离即可,按下右键拖动
else if(g_xform_mode == TRANSFORM_TRANSLATE) //平移
{//TODO:添加鼠标移动控制模型平移参数的代码
g_x_offset += (x - g_press_x) * 0.002f;
g_y_offset += -(y - g_press_y) * 0.002f;
g_press_x = x;
g_press_y = y;
}
缩放
缩放与平移相似,按下滚轮键滑动鼠标
else if(g_xform_mode == TRANSFORM_SCALE) //缩放
{//TODO:添加鼠标移动控制模型缩放参数的代码
g_scale_size += (x - g_press_x) * 0.01f;
}
至此,我们的鼠标交互也实现完了,下面就来试试效果
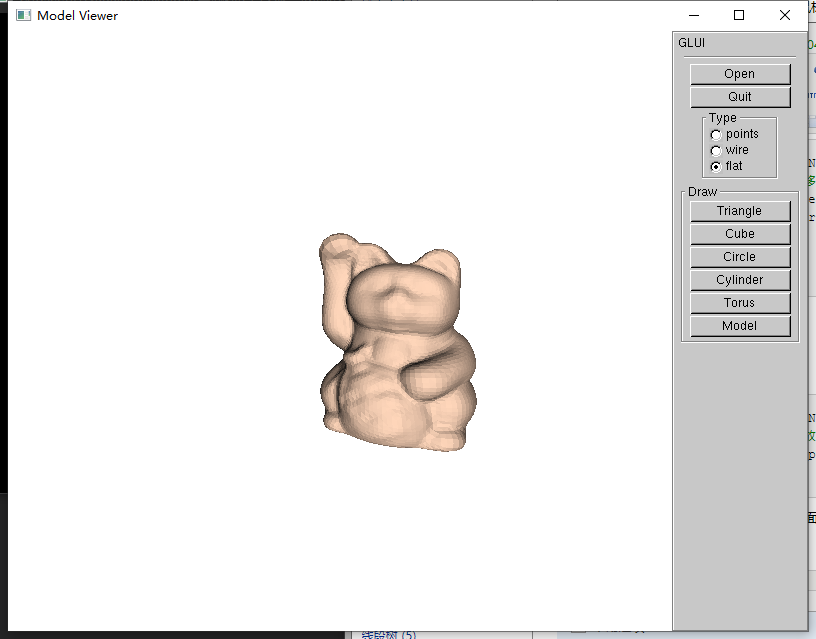
小节
这样,模型的加载及鼠标交互也就介绍完了,但是是不是还缺些什么?好像这个模型跟想象当中的还是有很大区别的,表面的图案呢??下一篇将介绍纹理贴图和曲线绘制。
从零开始openGL——三、模型加载及鼠标交互实现的更多相关文章
- OpenGL OBJ模型加载.
在我们前面绘制一个屋,我们可以看到,需要每个立方体一个一个的自己来推并且还要处理位置信息.代码量大并且要时间.现在我们通过加载模型文件的方法来生成模型文件,比较流行的3D模型文件有OBJ,FBX,da ...
- 6_1 持久化模型与再次加载_探讨(1)_三种持久化模型加载方式以及import_meta_graph方式加载持久化模型会存在的变量管理命名混淆的问题
笔者提交到gitHub上的问题描述地址是:https://github.com/tensorflow/tensorflow/issues/20140 三种持久化模型加载方式的一个小结论 加载持久化模型 ...
- 一步一步开发Game服务器(三)加载脚本和服务器热更新(二)完整版
上一篇文章我介绍了如果动态加载dll文件来更新程序 一步一步开发Game服务器(三)加载脚本和服务器热更新 可是在使用过程中,也许有很多会发现,动态加载dll其实不方便,应为需要预先编译代码为dll文 ...
- DirectX11 With Windows SDK--19 模型加载:obj格式的读取及使用二进制文件提升读取效率
前言 一个模型通常是由三个部分组成:网格.纹理.材质.在一开始的时候,我们是通过Geometry类来生成简单几何体的网格.但现在我们需要寻找合适的方式去表述一个复杂的网格,而且包含网格的文件类型多种多 ...
- Entity Framework关联实体的三种加载方法
推荐文章 EF性能之关联加载 总结很好 一:介绍三种加载方式 Entity Framework作为一个优秀的ORM框架,它使得操作数据库就像操作内存中的数据一样,但是这种抽象是有性能代价的,故鱼和熊掌 ...
- EF三种加载方法
EF性能之关联加载 鱼和熊掌不能兼得 ——中国谚语 一.介绍 Entity Framework作为一个优秀的ORM框架,它使得操作数据库就像操作内存中的数据一样,但是这种抽象是有性能代价的,故鱼和 ...
- cesium模型加载-加载fbx格式模型
整体思路: fbx格式→dae格式→gltf格式→cesium加载gltf格式模型 具体方法: 1. fbx格式→dae格式 工具:3dsMax, 3dsMax插件:OpenCOLLADA, 下载地址 ...
- Wish3D用户必看!模型加载失败原因汇总
上传到Wish3D的模型加载不出来,作品显示页面漆黑一片,是什么原因? 很有可能是操作过程中的小失误,不妨从以下几点检查.还是不行的请加QQ群(Wish3D交流群3):635725654,@Wish3 ...
- PyTorch模型加载与保存的最佳实践
一般来说PyTorch有两种保存和读取模型参数的方法.但这篇文章我记录了一种最佳实践,可以在加载模型时避免掉一些问题. 第一种方案是保存整个模型: 1 torch.save(model_object, ...
随机推荐
- 结合参数接收响应转换原理讲解SpringBoot常用注解
一.常用注解回顾 1.1 @RequestBody与@ResponseBody //注意并不要求@RequestBody与@ResponseBody成对使用. public @ResponseBody ...
- JMeter的安装部署——Linux系统
1.配置Java环境 在官网https://www.oracle.com/technetwork/java/javase/downloads/jdk10-downloads-4416644.html下 ...
- nyoj 122-Triangular Sums (数学之读懂求和公式的迭代)
122-Triangular Sums 内存限制:64MB 时间限制:3000ms 特判: No 通过数:5 提交数:7 难度:2 题目描述: The nth Triangular number, T ...
- 01-MongoDB数据库基础
一.MongoDB数据库基础 1.MongoDB数据库介绍 什么是MongoDB? MongoDB是非关系型数据库中的一种,是由C++语言编写的,是一个基于分布式文件存储的开源数据库系统.在高负载的情 ...
- [Part 3] 在Ubuntu 16.04源码编译PCL 1.8.1支持VTK和QT
本文首发于个人博客https://kezunlin.me/post/137aa5fc/,欢迎阅读! Part-3: Install and Configure PCL 1.8.1 with vtk q ...
- [Odoo12基础教程]之第零篇-win中odoo12环境搭建
所需材料 1.python3.7 2.pycharm社区版及以上 3.postgresSQL10 下载链接:https://www.enterprisedb.com/thank-you-downloa ...
- 在idea中使用git
在idea中使用git 1. 在idea中配置git 安装好IntelliJ IDEA后,如果Git安装在默认路径下,那么idea会自动找到git的位置,如果更改了Git的安装位置则需要手动配置下 ...
- Java8 Stream终端操作使用详解
话不多说,自己挖的坑自己要填完,今天就给大家讲完Java8中Stream的终端操作使用详解.Stream流的终端操作主要有以下几种,我们来一一讲解. forEach() forEachOrdered( ...
- .NET Core开发的iNeuOS工业互联网平台,发布 iNeuDA 数据分析展示组件,快捷开发图形报表和数据大屏
目 录 1. 概述... 2 2. 演示信息... 2 3. 简单介绍... 3 4. 产品特点... 4 5. 价值体现... 5 1. ...
- Djangoday2第二个app加减法
第二个app 计算新建一个app在view定义显示的内容修改urls指定连接对应的视图测试另一种通过路径传参的方式访问网址路径传参的urls定义方法网址路径传参测试urls的urlnamedjango ...
