linux bash编程之算数运算和测试类型（第二篇）

　　写在最前边：在bash中数据类型有两种，分别是数值型和字符型。其中字符型是默认的。

1、算数运算

　　· 运算符

　　· 语法

　　1.1、运算符：+、-、*、/、%、**

　　　　注意：有些时候 *（乘号）需要转义

　　1.2、语法：有以下几种方式

　　　　VAR为变量名，expression为算数表达式

　　　　let VAR=expression

　　　　VAR=$[expression]

　　　　VAR=$((expression))

　　　　VAR=$(expr argu1 argu2 argu3)

　　　　语法示例

　　　　

2、增强型赋值运算：在自身基础上做赋值运算

　　· 运算符

　    · 语法

　　2.1运算符：+=、-=、*=、/=、%=，++，--

　　2.2语法：

　　　　let i=$i+n ——>let i+=n

　　　　自增：let i=i+1 ——> let i++

　　　　自减：let i=i-1 ——>let i--

　　　　自增示例:

　　　　

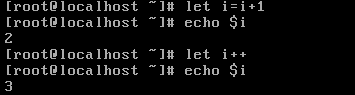
3、条件测试:编写测试机制来判断条件是否满足

　　· 利用命令的返回值来判断

　　· 测试表达式判断

　　· 组合测试条件

　　

　　3.1、利用命令的返回值来判断：执行一条命令他的运行结果可以使用echo $?查看

　　　　0：成功

　　　　1-255：失败

　　3.2、测试表达式判断

　　　　· 语法

　　　　· 测试类型

　　　　3.2.1、语法：

　　　　　　test expression ：test为关键字

　　　　　　[ expression ]：expression两边必须有空格

　　　　　　[[ expression ]]：expression两边必须有空格

　　　　3.2.2、测试类型：数值测试、字符串测试、文件测试

　　　　　　数值测试：数值比较

　　　　　　　　-eq：是否等于（equal）

　　　　　　　　-ne：是否不等于（not equal）

　　　　　　　　-gt：是否大于（greater than）

　　　　　　　　-ge:是否大于等于（greater equal）　　　

　　　　　　　　-lt：是否小于（little than）

　　　　　　　　-le：是否小于等于（little equal）

　　　　　　　　数值测试示例

　　　　　　　　

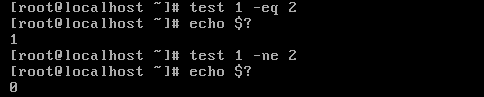
　　　　　　字符串测试：字符串要用引号引起来，最好使用[[ expression ]]

　　　　　　　　==：是否等于

　　　　　　　　!=：是否不等于

　　　　　　　　>：是否大于

　　　　　　　　<：是否小于

　　　　　　　　=~：左侧字符串是否能被右侧的pattern所匹配

　　　　　　　　-z：判断指定字符串是否为空。空为真，不空为假

　　　　　　　　-n：判断指定字符串是否不空。不空为真，空为假

　　　　　　字符串测试示例：

　　　　　　　　

　　　　　　　　由一下三个命令可以看出只有[[ "a" > "b" ]]返回值是正确的所有字符串要引起来切使用[[ expression ]]

　　　　　　

　　　　　　　　-z和-n使用示例

　　　　　　　　

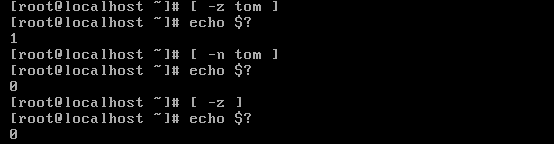
　　　　　　文件测试：

　　　　　　　　存在性测试：存在为真不存在为假

　　　　　　　　　　-a FILE

　　　　　　　　　　 -e FILE

　　　　　　　　文件类型测试

　　　　　　　　　　-b FILE：文件是否存在，且文件类型为块设备文件

　　　　　　　　　　-c  FILE：文件是否存在，且文件类型为字符设备文件

　　　　　　　　　　-d FILE：文件是否存在，且为目录文件

　　　　　　　　　　-f  FILE：文件是否存在，且为普通文件

　　　　　　　　　　-h 或-L FILE：文件是否存在，且为符号链接文件

　　　　　　　　　　-p FILE：文件是否存在，且为命名管道文件

　　　　　　　　　   -S FILE：文件是否存在，且为套接字文件

　　　　　　　　文件权限测试

　　　　　　　　　　-r FILE：文件是否存在，且对当前用户可读

　　　　　　　　　   -w FILE：文件是否存在，且对当前用户可写

　　　　　　　　　　-x FILE：文件是否存在，且对当前用户可执行

　　　　　　　　特殊权限测试：

　　　　　　　　　　-u FILE ：文件是否存在，且拥有suid权限。

　　　　　　　　　　-g FILE：文件是否存在，且拥有guid权限。

　　　　　　　　　　-k FILE：文件是否存在，且拥有sticky权限。

　　　　　　　　文件是否有内容

　　　　　　　　　　-s FILE ：是否不空。

　　　　　　　　时间戳：

　　　　　　　　　　-N FILE：文件自上一次读操作后是否被修改过。

　　　　　　　　从属关系测试：

　　　　　　　　　　-O：当前文件是否为文件的属主。

　　　　　　　　　　-G：当前用户是否属于文件的数组。

　　　　　　　　双目运算：文件新旧测试

　　　　　　　　　　FILE1 -ef FILE2：两个文件是否只想同一个文件系统的相同inode的硬链接

　　　　　　　　　　FILE1 -nt FILE2：文件1是否比文件2新

　　　　　　　　　　FILE1 -ot FILE2：文件1是否比文件2旧

　　3.3、组合测试条件：

　　　　逻辑运算：有两种方式

　　　　　　第一种

　　　　　　　　COMMAND1 && COMMAND2

　　　　　　　　COMMAND1 || COMMAND2

　　　　　　　　!COMMAND

　　　　　　第二种

　　　　　　　　EXPRESSION1 -a  EXPRESSION2

　　　　　　　　EXPRESSION1 -o  EXPRESSION2

　　　　　　　　!EXPRESSION

　　组合测试练习：将当前主机名保存在nameHost中，若主机名为空或者主机名为localhost.localdomain，则修改主机名为master

　　　　

shell编程其他文章请点击下边链接

• https://www.cnblogs.com/wxxjianchi/