【XSY2484】mex

Description

给你一个无限长的数组，初始的时候都为0，有3种操作：

操作1是把给定区间[l,r] 设为1，

操作2是把给定区间[l,r] 设为0，

操作3把给定区间[l,r] 0,1反转。

一共n个操作，每次操作后要输出最小位置的0。

Input

第一行一个整数n，表示有n个操作

接下来n行，每行3个整数op,l,r表示一个操作

Output

共n行，一行一个整数表示答案

Sample Input

3
1 3 4
3 1 6
2 1 3

Sample Output

1
3
1

HINT

对于30%的数据1≤n≤1000,1≤l≤r≤1e18

对于100%的数据1≤n≤100000,1≤l≤r≤1e18

l,r最大可达1e18，肯定要离散化。

有大量的区间修改的操作——考虑线段树

解决方法：

离散化+线段树

首先离散化。

离散化时将每一次操作的区间的l，r，r+1放入一个数组。lower_bound离散化，得到离散化后的l,r。

为什么要放入r+1？

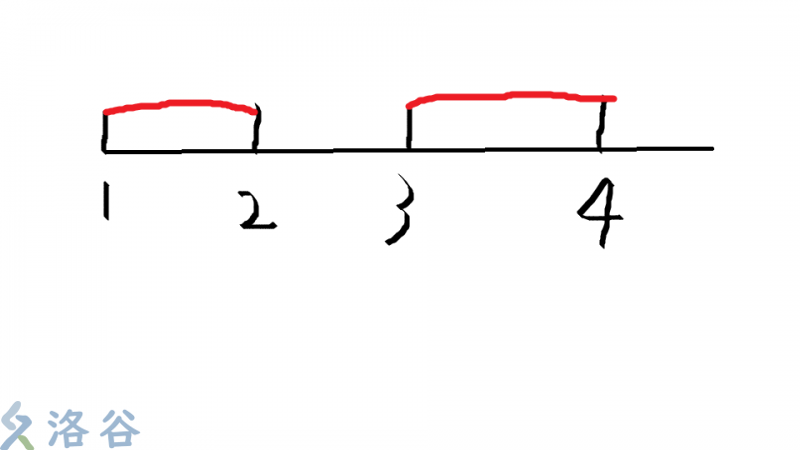
像这样，离散化后，1-2,3-4区间都为1，本来应该有0的存在，但在线段树上却没有，这时候就要用r+1把这个“坑”给填上。

离散化后：

线段树记录\(minn[i][0]\),\(minn[i][1]\),表示在该区间0和1最早在哪个点出现，若没出现过，minn=INF;

操作1,2： 区间修改\(minn[i][0]\),\(minn[i][1]\),\(sum[i]\)懒标记。

操作3： 交换\(minn[i][0]\),\(minn[i][1]\),\(lazy[i]\)懒标记记录是否换了回来，若没换回来，pushdown。

总体的思路就是这样了，代码有点难调试，一定要耐心打，用心调。

#include<bits/stdc++.h>
#define inf 1e9
using namespace std;
struct data
{
	int op;
	long long l,r;
}q[2000001];
int lazy[2000001],minn[2000001][2],sum[2000001],op,n,cnt,cnt1;
long long l,r,b[2000001];
void build(int hao,int l,int r)
{
	lazy[hao]=0;
	sum[hao]=-1;
	minn[hao][0]=l;
	minn[hao][1]=inf;
	if(l==r)
	{
		return;
	}
	int mid=(l+r)/2;
	build(hao<<1,l,mid);
	build(hao<<1|1,mid+1,r);
}
void pushdown(int hao,int l,int r)
{
	int mid=(l+r)/2;
	if(sum[hao]!=-1)//下放sum
	{
		int p=sum[hao];
		sum[hao<<1]=sum[hao<<1|1]=p;
		lazy[hao<<1]=lazy[hao<<1|1]=0;
		minn[hao<<1][p]=l;
		minn[hao<<1|1][p]=mid+1;
		minn[hao<<1][p^1]=inf;
		minn[hao<<1|1][p^1]=inf;
		sum[hao]=-1;
	}
	if(lazy[hao])//下放lazy
	{
		lazy[hao<<1]^=1;
		lazy[hao<<1|1]^=1;
		swap(minn[hao<<1][0],minn[hao<<1][1]);
		swap(minn[hao<<1|1][0],minn[hao<<1|1][1]);
		lazy[hao]=0;
	}
}
void update(int hao,int l,int r,int L,int R,int num)//操作1,2
{
	if(L<=l&&R>=r)
	{
		sum[hao]=num;
		minn[hao][num]=l;
		lazy[hao]=0;
		minn[hao][num^1]=inf;
	}else{
		pushdown(hao,l,r);
		int mid=(l+r)/2;
		if(L<=mid)
		{
			update(hao<<1,l,mid,L,R,num);
		}
		if(R>mid)
		{
			update(hao<<1|1,mid+1,r,L,R,num);
		}
		minn[hao][0]=min(minn[hao<<1][0],minn[hao<<1|1][0]);
		minn[hao][1]=min(minn[hao<<1][1],minn[hao<<1|1][1]);
	}
}
void change(int hao,int l,int r,int L,int R)//操作3
{
	if(L<=l&&R>=r)
	{
		lazy[hao]^=1;
		swap(minn[hao][0],minn[hao][1]);
	}else{
		pushdown(hao,l,r);
		int mid=(l+r)/2;
		if(L<=mid)
		{
			change(hao<<1,l,mid,L,R);
		}
		if(R>mid)
		{
			change(hao<<1|1,mid+1,r,L,R);
		}
		minn[hao][0]=min(minn[hao<<1][0],minn[hao<<1|1][0]);
		minn[hao][1]=min(minn[hao<<1][1],minn[hao<<1|1][1]);
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%lld%lld",&op,&l,&r);
		q[i].op=op;
		q[i].l=l;
		q[i].r=r;
		b[++cnt]=l;
		b[++cnt]=r;
		b[++cnt]=r+1;
	}
	b[++cnt]=1;
	sort(b+1,b+cnt+1);
	b[0]=-0x7f7f7f7f;
	for(int i=1;i<=cnt;i++)//去重
	{
		if(b[i]==b[i-1])
		{
			continue;
		}
		b[++cnt1]=b[i];
	}
	cnt=cnt1;
	build(1,1,cnt);
	for(int i=1;i<=n;i++)
	{
		int l=lower_bound(b,b+cnt+1,q[i].l)-b;//离散化
		int r=lower_bound(b,b+cnt+1,q[i].r+1)-b-1;
		if(q[i].op==1)
		{
			update(1,1,cnt,l,r,1);
		}else{
			if(q[i].op==2)
			{
				update(1,1,cnt,l,r,0);
			}else{
				change(1,1,cnt,l,r);
			}
		}
		printf("%lld\n",b[minn[1][0]]);
	}
	return 0;
}
/*
3
1 3 4
3 1 6
2 1 3
*/