UVA11374 Airport Express 正反两次最短路

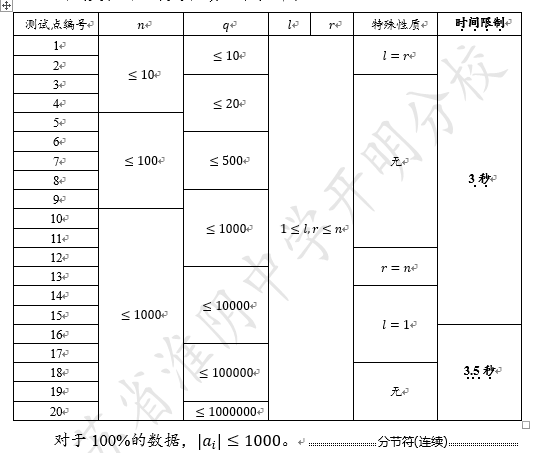
问题描述

洛谷（有翻译）

---

吐槽

一道坑题。

---

如何对待商务票

因为商务票只有一张，所以在\(k\)条边中只有一条边会被选中，很显然，最后这条边会被枚举。

---

如何选择使用商务票的边

假设我们正在枚举这条边，现在的边为\((u,v)\)，边权为\(w\)。

那么现在的最小代价肯定为

\[min(dist_{(s,u)_{min}}+dist_{(v,e)_{min}}+w,dist_{(s,v)_{min}}+dist_{(u,e)_{min}}+w)
\]

其中\(s\)代表起点，\(e\)代表终点，\(dist_{(a,b)}\)代表\(a\)到\(b\)的距离。

从\(dist_{(a,b)_{min}}\)中，我们可以很清楚地感受到，需要跑最短路。

强烈推荐使用\(dijkstra\)+堆优化。

如果你不确定你的最短路模板是否正确，请移步

---

两次最短路

经过分析，我们知道要跑最短路，但是由于有两个点分别到\(s\)和\(e\)的最短距离，那么就需要以\(s\)和\(e\)分别为源，跑单源最短路径。

最短路中需要记录前驱。

---

总思路

先读入，注意多组测试数据。

再跑两遍最短路。

枚举\(k\)条边，对于每一条边\((u,v)\)，用上面的公式和当前最优的\(ans\)比较并记录。

最后输出。（如果挂了先调这个）

---

细节

• 每组测试数据的输出之间需要一个空行

• 最后一组测试数据后不能有空行

• 行末不能有多余的空格

---

彩蛋

点这里

可能有点卡

---

代码

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;

#define maxn 500
#define maxm 1000
struct node{
    int dis,x;
    bool operator <(const node &a)const
    {
        return dis>a.dis;
    }
};
int h_j[maxn+7],n_j[maxm*2+7],h_s[maxn+7],n_s[maxm*2+7],u_j[maxm*2+7],v_j[maxm*2+7],w_j[maxm*2+7],tot_j,u_s[maxm*2+7],v_s[maxm*2+7],w_s[maxm*2+7],tot_s;
int s,e,n,m,k,x,y,z,p[maxn+7],dis1[maxn+7],dis2[maxn+7],qi1[maxn+7],qi2[maxn+7],ans=0x7fffffff,ansi,ansj;
bool used1[maxn+7],used2[maxn+7];
int u[maxm+7],v[maxm+7],w[maxm+7],stac[maxn+7],cas,xx,top;
void add_j()
{
    u_j[++tot_j]=x,v_j[tot_j]=y,w_j[tot_j]=z;
    n_j[tot_j]=h_j[x],h_j[x]=tot_j;
    u_j[++tot_j]=y,v_j[tot_j]=x,w_j[tot_j]=z;
    n_j[tot_j]=h_j[y],h_j[y]=tot_j;
}
void clear()
{
    memset(h_j,0,sizeof(h_j));
    memset(n_j,0,sizeof(n_j));
    memset(used1,0,sizeof(used1));
    memset(used2,0,sizeof(used2));
    tot_j=0;
    memset(qi1,0,sizeof(qi1));
    memset(qi2,0,sizeof(qi2));
    ans=0x7fffffff;
}
int mian()
{
    while((~scanf("%d%d%d",&n,&s,&e))&&n&&s&&e)
    {
        if(cas++) printf(" ");
        clear();
        scanf("%d",&m);
        for(register int i=1;i<=m;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            add_j();
        }
        scanf("%d",&k);
        for(register int i=1;i<=k;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            u[i]=x,v[i]=y,w[i]=z;
        }
        for(register int i=1;i<=n;i++) dis1[i]=dis2[i]=0x3f3f3f3f;
        priority_queue<node>q1;
        dis1[s]=0;
        q1.push((node){0,s});
        while(!q1.empty())
        {
            int u=q1.top().x;
            q1.pop();
            if(used1[u]) continue;
            used1[u]=1;
            for(int i=h_j[u];i;i=n_j[i])
            {
                int aa=v_j[i],co=w_j[i];
                if(dis1[aa]>dis1[u]+co)
                {
                    dis1[aa]=dis1[u]+co;qi1[aa]=u;
                    q1.push((node){dis1[aa],aa});
                }
            }
        }
        priority_queue<node>q2;
        dis2[e]=0;
        q2.push((node){0,e});
        while(!q2.empty())
        {
            int u=q2.top().x;
            q2.pop();
            if(used2[u]) continue;
            used2[u]=1;
            for(int i=h_j[u];i;i=n_j[i])
            {
                int aa=v_j[i],co=w_j[i];
                if(dis2[aa]>dis2[u]+co)
                {
                    dis2[aa]=dis2[u]+co;qi2[aa]=u;
                    q2.push((node){dis2[aa],aa});
                }
            }
        }
        for(register int i=1;i<=k;i++)
        {
            if(dis1[u[i]]+dis2[v[i]]+w[i]<=ans)
            {
                ans=dis1[u[i]]+dis2[v[i]]+w[i];
                ansi=u[i];
                ansj=v[i];
            }
            if(dis1[v[i]]+dis2[u[i]]+w[i]<=ans)
            {
                ans=dis1[v[i]]+dis2[u[i]]+w[i];
                ansi=v[i];
                ansj=u[i];
            }
        }
        xx=ansi;
        top=0;
        if(s==e)
        {
            printf("%d\nTicket Not Used\n0\n",s);
            continue;
        }
        if(ans<=dis1[e])
        {
            while(xx!=s&&xx)
            {
                stac[++top]=xx;
                xx=qi1[xx];
            }
            printf("%d ",s);
            while(top)
            {
                printf("%d ",stac[top--]);
            }
            xx=ansj;
            while(xx!=e&&xx)
            {
                stac[++top]=xx;
                xx=qi2[xx];
            }
            int fuck=1;
            while(fuck<=top)
            {
                printf("%d ",stac[fuck++]);
            }
            printf("%d\n",e);
            printf("%d\n%d\n",ansi,ans);
        }
        else
        {
            int xx=qi1[e];
            while(xx!=s&&xx)
            {
                stac[++top]=xx;
                xx=qi1[xx];
            }
            printf("%d ",s);
            while(top)
            {
                printf("%d ",stac[top--]);
            }
            printf("%d\nTicke Not Used\n%d\n",e,dis1[e]);
        }
    }
}