2D空间中求一点是否在多边形内
参考自这篇博文:http://www.cnblogs.com/dabiaoge/p/4491540.html
一开始没仔细看做法,浪费了不少时间。下面是最终实现的效果:

大致流程:
1.随便选取多边形上任意一条边,以比较点和边的中心点做一条射线(这里用的伪射线)。
2.用这条射线与其他所有边判断是否相交。
3.将所有与线段相交的数量相加,如果是奇数就在多边形内。
特殊情况:
1.刚好在点上或者在线上。实际运用时会有点误差,但不影响。
2.必须是闭合线段,且不能存在包含的情况。但如果是一个数组生成的线段,不会有这种情况
代码(Unity3D):
using UnityEngine;
using System.Collections; public class Test1 : MonoBehaviour
{
const float RAYCAST_LEN = 100000f;
public Transform[] points;
public Transform compare; bool IsContract(Transform compare)
{
var comparePoint = (points[].position + points[].position) * 0.5f;
var originPoint = compare.transform.position;
comparePoint += (comparePoint - originPoint).normalized * RAYCAST_LEN; Debug.DrawLine(originPoint, comparePoint); int count = ;
for (int i = ; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + ) % points.Length]; var r = IsIntersection(a.position, b.position, originPoint, comparePoint); if (r) count++;
} return count % == ;
} void OnDrawGizmos()
{
if (compare == null) return; var oldColor = Gizmos.color; if (IsContract(compare))
Gizmos.color = Color.red; for (int i = ; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + ) % points.Length]; Gizmos.DrawLine(a.position, b.position);
} Gizmos.color = oldColor;
} bool IsIntersection(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
{
var crossA = Mathf.Sign(Vector3.Cross(d - c, a - c).y);
var crossB = Mathf.Sign(Vector3.Cross(d - c, b - c).y); if (Mathf.Approximately(crossA, crossB)) return false; var crossC = Mathf.Sign(Vector3.Cross(b - a, c - a).y);
var crossD = Mathf.Sign(Vector3.Cross(b - a, d - a).y); if (Mathf.Approximately(crossC, crossD)) return false; return true;
}
}
另外参考的文章中没有说差乘判断两个线段是否相交的具体做法,这里说明一下
大致流程:
现在有线段AB和线段CB
用线段AB的方向和C,D两点分别做差乘比较。如果C,D在同侧则return跳出
用线段CD的方向和A,B两点分别做差乘比较。如果A,B在同侧则return跳出
最终返回相交
脚本就是上面的IsIntersection函数,最终实现效果(只适用于2D空间,如果是XY轴向要取差乘的z分量做比较):
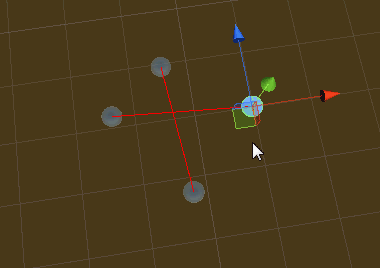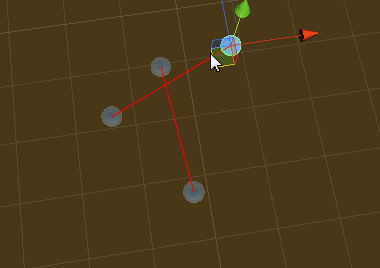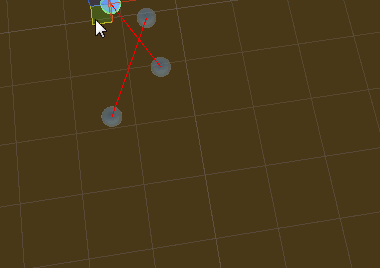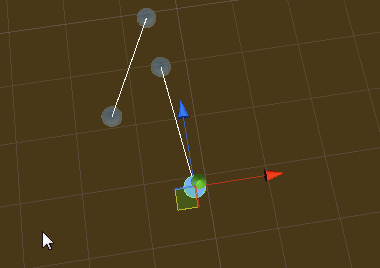
2D空间中求一点是否在多边形内的更多相关文章
- 2D空间中判断一点是否在三角形内
要注意如果是XY坐标轴的2D空间,要取差乘分量z而不是y. 实现原理是,将三角形ABC三个边(AB,BC,CA)分别与比较点判断差乘,如果这3个差乘结果表示的方向一致,说明就在三角形内. 效果: 代码 ...
- 2D空间中求两圆的交点
出处:https://stackoverflow.com/questions/19916880/sphere-sphere-intersection-c-3d-coordinates-of-colli ...
- 2D空间中求线段与圆的交点
出处: https://answers.unity.com/questions/366802/get-intersection-of-a-line-and-a-circle.html 测试脚本(返回值 ...
- [译]2D空间中使用四叉树Quadtree进行碰撞检测优化
操作系统:Windows8.1 显卡:Nivida GTX965M 开发工具:Unity2017.2.0f3 原文出处 : Quick Tip: Use Quadtrees to Detect Lik ...
- 2d游戏中求出一个向量的两个垂直向量
function cc.exports.VerticalVector(vec)--求出两个垂直向量 local result = {} result[1] = cc.p(vec.y/vec.x,-1) ...
- 2D和3D空间中计算两点之间的距离
自己在做游戏的忘记了Unity帮我们提供计算两点之间的距离,在百度搜索了下. 原来有一个公式自己就写了一个方法O(∩_∩)O~,到僵尸到达某一个点之后就向另一个奔跑过去 /// <summary ...
- Computer Science Theory for the Information Age-2: 高维空间中的正方体和Chernoff Bounds
高维空间中的正方体和Chernoff Bounds 本文将介绍高维空间中正方体的一些性质,以及一个非常常见也是非常有用的概率不等式——Chernoff Bounds. 考虑$d$维单位正方体$C=\{ ...
- Computer Science Theory for the Information Age-1: 高维空间中的球体
高维空间中的球体 注:此系列随笔是我在阅读图灵奖获得者John Hopcroft的最新书籍<Computer Science Theory for the Information Age> ...
- 为什么很多人坚信“富贵险中求”?
之家哥 2017-11-15 09:12:31 微信QQ微博 下载APP 摘要 网贷之家小编根据舆情频道的相关数据,精心整理的关于<为什么很多人坚信"富贵险中求"?>的 ...
随机推荐
- Aspose Cells 添加数据验证(动态下拉列表验证)
参考 :http://www.componentcn.com/kongjianjishu/kongjianjishu/2015-06-04/2781.html Aspose Cells是一款操作和处理 ...
- GIT与SVN的区别
1.GIT是分布式的,SVN不是: 这是GIT和其它非分布式的版本控制系统,例如SVN,CVS等,最核心的区别.如果你能理解这个概念,那么你就已经上手一半了.需要做一点声明,GIT并不是目前第一个或唯 ...
- Beta阶段站立会议-01
组名:金州勇士 组长:尹良亮 组员:王汉斌.杜月.闫浩楠 代码地址: ssh:git@git.coding.net:handsomeman/examm.githttps://git.coding.ne ...
- IOS第二天多线程-02一次性代码
********** #import "HMViewController.h" #import "HMImageDownloader.h" @interface ...
- 整形输出netsh的内容
$raw = netsh wlan show network mode=bssid $ssids = $raw | Select-String -Pattern 'SSID\b'| Select-St ...
- springmvc Failed to load resource: the server responded with a status of 404 (Not Found)
jsp页面导入css.js提示上述问题. Spring对静态资源的请求做专门处理 <!-- 对静态资源的请求 --><mvc:resources location="/js ...
- NEC学习 ---- 模块 - 上图下文图文列表
上图下文图文列表的效果如下图: 可以看到三个红色框中的三中"上图下文的图文列表"; 这里的代码其实没什么问题, 对于这种布局, 其实可以参考我上一篇介绍: NEC学习 ---- 模 ...
- AFNetworking 提示"The resource could not be loaded because the App Transport Security policy requires the use of a secure connection" 解决办法
原因:iOS9以后,苹果把原http协议改成了https协议,所以不能直接在http协议下GET/POST 解决方案之一: 直接编辑工程文件下的Info.plist文件,加入以下代码 <key& ...
- A B-tree index can be used for column comparisons in expressions that use the =, >, >=, <, <=, or BETWEEN operators.
http://dev.mysql.com/doc/refman/5.7/en/index-btree-hash.html MySQL 5.7 Reference Manual / ... / ...
- CentOS7配置日志(VirtualBox)
版本为CentOS-Minimal 1.VirtualBox下安装CentOS. 新建虚拟机 下载CentOS,放入盘片,启动虚拟机,按提示开始安装(建议内存1G,硬盘10G以上) 2. 设置网络 ...
