字符串匹配(hash算法）

hash函数对大家来说不陌生吧 ？

而这次我们就用hash函数来实现字符串匹配。

首先我们会想一下二进制数。

对于任意一个二进制数，我们将它化为10进制的数的方法如下（以二进制数1101101为例）：

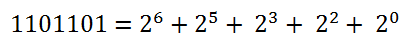
hash用的也是一样的原理，为每一个前缀（也可以后缀，笔者习惯1 base，所以喜欢用前缀来计算，Hash[i] = Hash[i - 1] * x + s[i](其中1 < i <= n,Hash[0] = 0)。

一般地，

而对于l - r区间的hash值，则为：

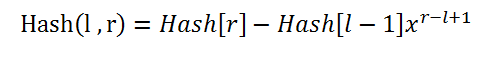
但是如果n很大呢？那样不是会溢出了吗？

因此我们把hash值储存在unsigned long long里面， 那样溢出时，会自动取余2的64次方，but这样可能会使2个不同串的哈希值相同，但这样的概率极低（不排除你的运气不好）。

因此我们可以通过Hash值来比较两个字符串是否相等。

给出多项式hash的处理：

typedef unsigned long long ull;
const int N = 100000 + 5;
const ull base = 163;
char s[N];
ull hash[N];
 
void init(){//处理hash值
    p[0] = 1;
    hash[0] = 0;
    int n = strlen(s + 1);
   for(int i = 1; i <=100000; i ++)p[i] =p[i-1] * base;
   for(int i = 1; i <= n; i ++)hash[i] = hash[i - 1] * base + (s[i] - 'a');
}
 
ull get(int l, int r, ull g[]){//取出g里l - r里面的字符串的hash值
    return g[r] - g[l - 1] * p[r - l + 1];
}

我们来看到题目吧：传送门

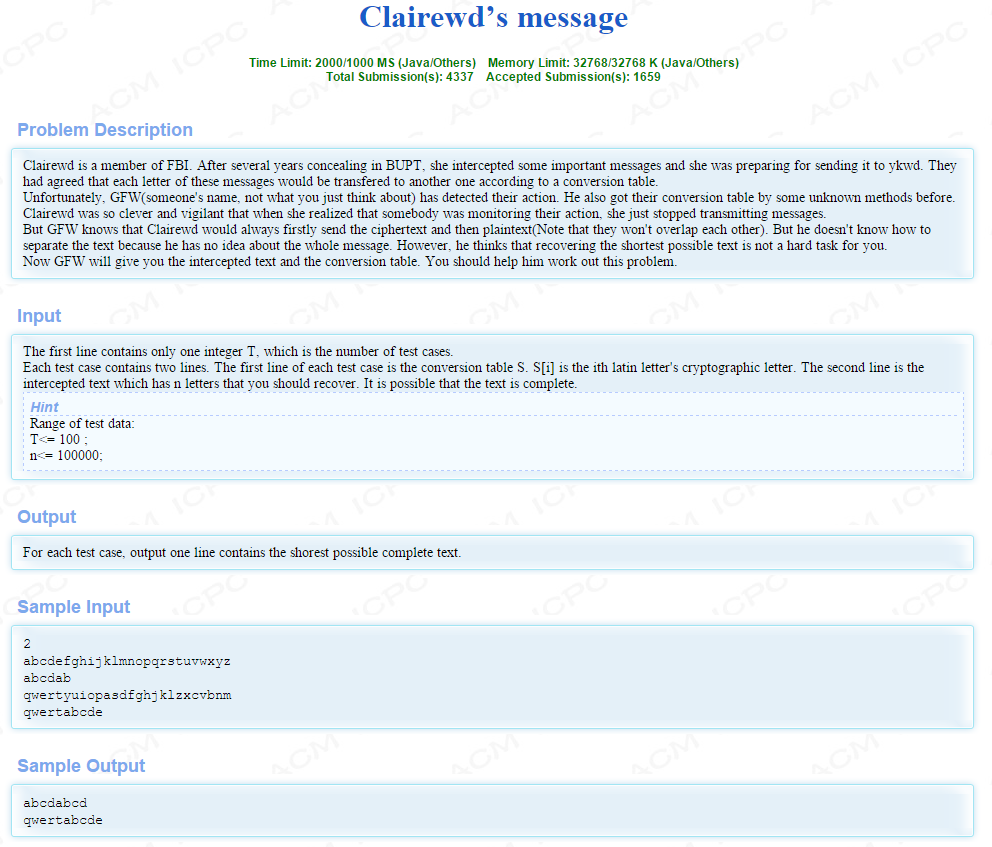
题目大意:

是有一份文件，前面是密文，后面是原文，但那个人接到这个文件后不知道中间从哪里开始是原文，所以你要帮忙还原一下，如果后面原文比密文少，你就将它补全, 第一行是密文转换格式，例如第二个样例表示将q翻译成a,w翻译成b。

思路：

我们只要先把密文都翻译成明文，然后去比较原来的字符串的后缀和翻译之后的字符串前缀的最长匹配长度就行（注：最长匹配的长度不能超过原长的一半）

hash水题（附AC代码）：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int N = 100000 + 5;
const ull base = 163;
ull Hash1[N], Hash2[N], p[N];
 
char s[N], t[30], r[N];
 
int T;
 
int c[30];
 
void init(){
    p[0] = 1;
   for(int i = 1; i <=100000; i ++)p[i] =p[i-1] * base;
}
 
ull get(int l, int r, ull g[]){
    return g[r] - g[l - 1]*p[r - l + 1];
}
 
void work(){
    for(int i = 0; i < 26; i ++) c[t[i] - 'a'] = i;
    //puts(r+1);
    int n = strlen(s + 1);
    Hash1[0] = Hash2[0] = 0;
    for(int i = 1; i <= n; i ++){
        Hash1[i] = Hash1[i - 1] * base + (s[i] - 'a');
        Hash2[i] = Hash2[i - 1] * base + (c[s[i] - 'a']);
    }
    int ans = n;
    for(int i = n; i < n * 2; i ++){
        if(i & 1) continue;
        int tmp = i / 2;
        int len =n - tmp;
        ull s1 = get(1, len, Hash2);
        ull s2 = get(n - len + 1, n, Hash1);
        if(s1 == s2){
            ans = tmp;
            break;
        }
        //printf("%llu %llu\n", s1, s2);
    }
    //printf("ans = %d\n", ans);
    for(int i = 1; i <= ans; i ++)printf("%c", s[i]);
    for(int i = 1; i <= ans; i ++)printf("%c", c[s[i]-'a'] + 'a');
    puts("");
}
 
int main(){
    scanf("%d", &T);
    init();
    while(T--){
        scanf("%s%s", t, s + 1);
        work();
    }
    return 0;
}