Deep Learning 4_深度学习UFLDL教程：PCA in 2D_Exercise（斯坦福大学深度学习教程）

前言

本节练习的主要内容：PCA，PCA Whitening以及ZCA Whitening在2D数据上的使用，2D的数据集是45个数据点，每个数据点是2维的。要注意区别比较二维数据与二维图像的不同，特别是在代码中，可以看出主要二维数据的在PCA前的预处理不需要先0均值归一化，而二维自然图像需要先0均值归一化。本节是在学习UFLDL第二节和结合上节的博文：Deep Learning三：预处理之主成分分析与白化_总结（斯坦福大学UFLDL深度学习教程）的基础上练习的，练习内容是Exercise:PCA in 2D，主要是讲二维数据的PCA、PCA白化、ZCA白化，下一节讲二维自然图像的PCA、PCA白化、ZCA白化。

实验环境：win7 matlab2015b

一些matlab函数

彩色分散点图函数：scatter(x,y,c,s) x, y为两个矢量，用于定位数据点，s为绘图点的大小，c为绘图所使用的色彩，s和c均可以以矢量或表达式形式给出，s和c为与x或y同长度的矢量时标记点尺 寸和颜色将按线性规律变化。在 scatter函数的前4各参数之后还可以增加第五个参数‘ filled‘，表示填充绘图点。Scatter与plot 的最大差别在于Scatter可以绘制变尺寸、变颜色的点图。
例：给定数据t=0:pi/10:2*pi, y=sin(t)，观察在不同输入参数时函数的绘图结果。
t=0:pi/10:2*pi; y=sin(t)
subplot(3,2,1); scatter(t,y)
subplot(3,2,2); scatter(t,y,'v')
subplot(3,2,3); scatter(t,y,(abs(y)+2).^4,'filled')
subplot(3,2,4); scatter(t,y,30,[0:2: 40],'v','filled')
subplot(3,2,5); scatter(t,y,(t+1).^3,y,'filled')

diag函数功能：矩阵对角元素的提取和创建对角阵

设以下X为方阵，v为向量

1、X = diag(v,k)当v是一个含有n个元素的向量时，返回一个n+abs(k)阶方阵X，向量v在矩阵X中的第k个对角线上，k=0表示主对角线，k>0表示在主对角线上方，k<0表示在主对角线下方。例1：

v=[1 2 3];
diag(v, 3)

ans =

0     0     0     1     0     0
     0     0     0     0     2     0
     0     0     0     0     0     3
     0     0     0     0     0     0
     0     0     0     0     0     0
     0     0     0     0     0     0

注：从主对角矩阵上方的第三个位置开始按对角线方向产生数据的

例2：

v=[1 2 3];
diag(v, -1)
ans =
      0 0 0 0
      1 0 0 0
      0 2 0 0
      0 0 3 0

注：从主对角矩阵下方的第一个位置开始按对角线方向产生数据的

2、X = diag(v)

向量v在方阵X的主对角线上，类似于diag(v,k),k=0的情况。

例3：

v=[1 2 3];
diag(v)

ans =

1 0 0
0 2 0
0 0 3

注：写成了对角矩阵的形式

3、v = diag(X,k)

返回列向量v，v由矩阵X的第k个对角线上的元素形成

例4：

v=[1 0 3;2 3 1;4 5 3];
diag(v,1)

ans =

0
     1

注：把主对角线上方的第一个数据作为起始数据，按对角线顺序取出写成列向量形式

4、v = diag(X)返回矩阵X的主对角线上的元素，类似于diag(X,k)，k=0的情况例5：

v=[1 0 0;0 3 0;0 0 3];
diag(v)

ans =

1
3
3

或改为：

v=[1 0 3;2 3 1;4 5 3];
diag(v)

ans =

1
3
3

注：把主对角线的数据取出写成列向量形式

5、diag(diag(X))

取出X矩阵的对角元，然后构建一个以X对角元为对角的对角矩阵。
例6：

X=[1 2;3 4]       
 diag(diag(X))

X =

1     2
     3     4

ans =

1     0
     0     4

实验步骤及结果

1.加载45个二维数据点，并用scatter函数显示出来。结果如下：

2.找到PCA的两个主方向，即：PCA的基，在原始数据上显示出来。先求出原始数据的协方差矩阵，再用svd函数求出该矩阵的特征向量，这就是要求的基。注意：对二维数据，其原始数据的预处理并没有0均值归一化。结果如下：

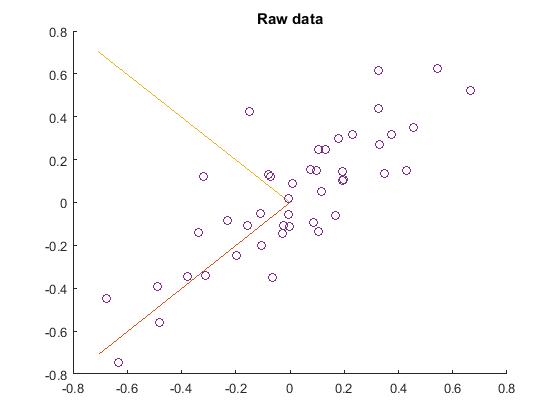
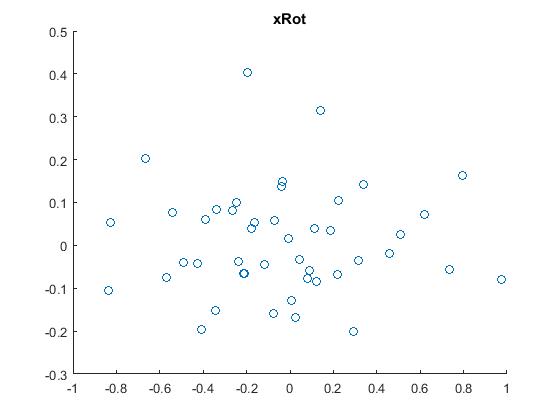
3.把原始数据映射（投影）或旋转到上一步所求的基方向上，得到数据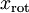 ，然后用scatter函数把它显示出来。结果如下：

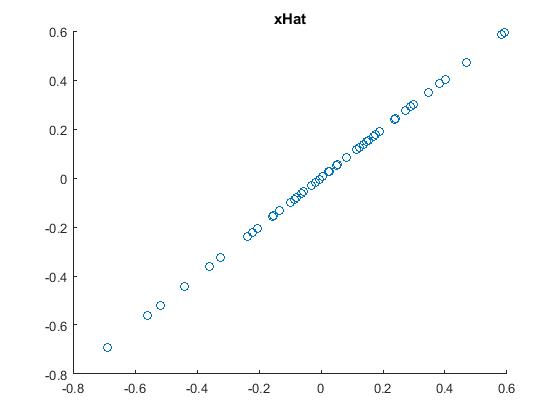
4.降维后近似还原原始数据，即：对上一步的数据结果降维，并显示出来。先计算设置要保留下来的主成份个数k，从而计算出降维后还原的原始数据 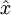。结果如下：

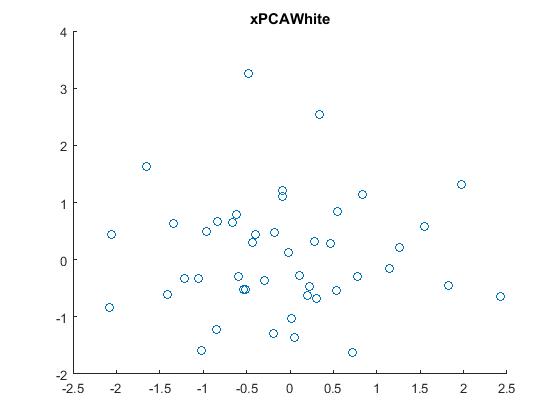
5.PCA白化，即把原始数据利用PCA whitening的方法去相关后，得到的原数据显示出来。结果如下：

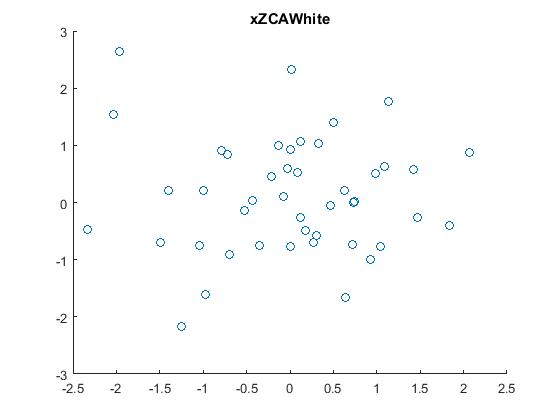
6.ZCA白化，即把原始数据利用ZCA whitening的方法去相关后，得到的原数据显示出来。结果如下：

代码

pca_2d.m

close all
 
%%================================================================
%% Step 0: Load data
%  We have provided the code to load data from pcaData.txt into x.
%  x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to
%  the kth data point.Here we provide the code to load natural image data into x.
%  You do not need to change the code below.
 
x = load('pcaData.txt','-ascii');
figure(1);
scatter(x(1, :), x(2, :));
title('Raw data');
 
%%================================================================
%% Step 1a: Implement PCA to obtain U
%  Implement PCA to obtain the rotation matrix U, which is the eigenbasis
%  sigma. 
 
% -------------------- YOUR CODE HERE --------------------
u = zeros(size(x, 1)); % You need to compute this
[n m] = size(x);
%x = x-repmat(mean(x,2),1,m);%预处理，均值为0
sigma = (1.0/m)*x*x';
[u s v] = svd(sigma);
 
% --------------------------------------------------------
hold on
plot([0 u(1,1)], [0 u(2,1)]);%画第一条线
plot([0 u(1,2)], [0 u(2,2)]);%第二条线
scatter(x(1, :), x(2, :));
hold off
 
%%================================================================
%% Step 1b: Compute xRot, the projection on to the eigenbasis
%  Now, compute xRot by projecting the data on to the basis defined
%  by U. Visualize the points by performing a scatter plot.
 
% -------------------- YOUR CODE HERE --------------------
xRot = zeros(size(x)); % You need to compute this
xRot = u'*x;
 
% -------------------------------------------------------- 
 
% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure(2);
scatter(xRot(1, :), xRot(2, :));
title('xRot');
 
%%================================================================
%% Step 2: Reduce the number of dimensions from 2 to 1.
%  Compute xRot again (this time projecting to 1 dimension).
%  Then, compute xHat by projecting the xRot back onto the original axes
%  to see the effect of dimension reduction
 
% -------------------- YOUR CODE HERE --------------------
k = 1; % Use k = 1 and project the data onto the first eigenbasis
xHat = zeros(size(x)); % You need to compute this
xHat = u*([u(:,1),zeros(n,1)]'*x);
 
% --------------------------------------------------------
figure(3);
scatter(xHat(1, :), xHat(2, :));
title('xHat');
 
%%================================================================
%% Step 3: PCA Whitening
%  Complute xPCAWhite and plot the results.
 
epsilon = 1e-5;
% -------------------- YOUR CODE HERE --------------------
xPCAWhite = zeros(size(x)); % You need to compute this
xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x;
 
% --------------------------------------------------------
figure(4);
scatter(xPCAWhite(1, :), xPCAWhite(2, :));
title('xPCAWhite');
 
%%================================================================
%% Step 3: ZCA Whitening
%  Complute xZCAWhite and plot the results.
 
% -------------------- YOUR CODE HERE --------------------
xZCAWhite = zeros(size(x)); % You need to compute this
xZCAWhite = u*diag(1./sqrt(diag(s)+epsilon))*u'*x;
 
% --------------------------------------------------------
figure(5);
scatter(xZCAWhite(1, :), xZCAWhite(2, :));
title('xZCAWhite');
 
%% Congratulations! When you have reached this point, you are done!
%  You can now move onto the next PCA exercise. :)

　　二维数据：pcaData.txt

  -6.7644914e-01  -6.3089308e-01  -4.8915202e-01  -4.8005424e-01  -3.7842021e-01  -3.3788391e-01  -3.2023528e-01  -3.1108837e-01  -2.3145555e-01  -1.9623727e-01  -1.5678926e-01  -1.4900779e-01  -1.0861557e-01  -1.0506308e-01  -8.0899829e-02  -7.1157518e-02  -6.3251073e-02  -2.6007219e-02  -2.2553443e-02  -5.8489047e-03  -4.3935323e-03  -1.7309716e-03   7.8223728e-03   7.5386969e-02   8.6608396e-02   9.6406046e-02   1.0331683e-01   1.0531131e-01   1.1493296e-01   1.3052813e-01   1.6626253e-01   1.7901863e-01   1.9267343e-01   1.9414427e-01   1.9770003e-01   2.3043613e-01   3.2715844e-01   3.2737163e-01   3.2922364e-01   3.4869293e-01   3.7500704e-01   4.2830153e-01   4.5432503e-01   5.4422436e-01   6.6539963e-01
  -4.4722050e-01  -7.4778067e-01  -3.9074344e-01  -5.6036362e-01  -3.4291940e-01  -1.3832158e-01   1.2360939e-01  -3.3934986e-01  -8.2868433e-02  -2.4759514e-01  -1.0914760e-01   4.2243921e-01  -5.2329327e-02  -2.0126541e-01   1.3016657e-01   1.2293321e-01  -3.4787750e-01  -1.4584897e-01  -1.0559656e-01  -5.4200847e-02   1.6915422e-02  -1.1069762e-01   9.0859816e-02   1.5269096e-01  -9.4416463e-02   1.5116385e-01  -1.3540126e-01   2.4592698e-01   5.1087447e-02   2.4583340e-01  -5.9535372e-02   2.9704742e-01   1.0168115e-01   1.4258649e-01   1.0662592e-01   3.1698532e-01   6.1577841e-01   4.3911172e-01   2.7156501e-01   1.3572389e-01   3.1918066e-01   1.5122962e-01   3.4979047e-01   6.2316971e-01   5.2018811e-01

　　

参考资料：

http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973631.html

UFLDL教程