数据结构之DFS与BFS实现
本文主要包括以下内容
- 邻接矩阵实现无向图的BFS与DFS
- 邻接表实现无向图的BFS与DFS
理论介绍
深度优先搜索介绍
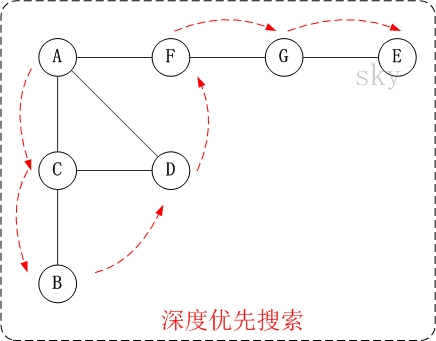
图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。
它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
显然，深度优先搜索是一个递归的过程。
广度优先搜索介绍
广度优先搜索算法(Breadth First Search)，又称为”宽度优先搜索”或”横向优先搜索”，简称BFS。
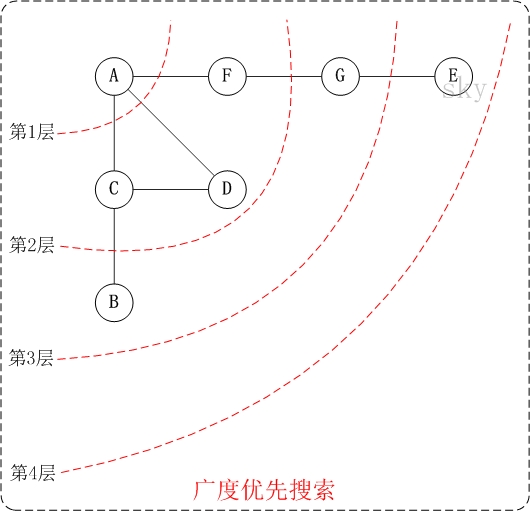
它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。
换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。
邻接矩阵实现无向图的BFS与DFS
/**
* C++: 邻接矩阵表示的"无向图(Matrix Undirected Graph)"
*
* @author skywang
* @date 2014/04/19
*/
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
#define MAX 100
class MatrixUDG {
private:
char mVexs[MAX]; // 顶点集合
int mVexNum; // 顶点数
int mEdgNum; // 边数
int mMatrix[MAX][MAX]; // 邻接矩阵
public:
// 创建图(自己输入数据)
MatrixUDG();
// 创建图(用已提供的矩阵)
MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);
~MatrixUDG();
// 深度优先搜索遍历图
void DFS();
// 广度优先搜索（类似于树的层次遍历）
void BFS();
// 打印矩阵队列图
void print();
private:
// 读取一个输入字符
char readChar();
// 返回ch在mMatrix矩阵中的位置
int getPosition(char ch);
// 返回顶点v的第一个邻接顶点的索引，失败则返回-1
int firstVertex(int v);
// 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
int nextVertex(int v, int w);
// 深度优先搜索遍历图的递归实现
void DFS(int i, int *visited);
};
/*
* 创建图(自己输入数据)
*/
MatrixUDG::MatrixUDG()
{
char c1, c2;
int i, p1, p2;
// 输入"顶点数"和"边数"
cout << "input vertex number: ";
cin >> mVexNum;
cout << "input edge number: ";
cin >> mEdgNum;
if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1))))
{
cout << "input error: invalid parameters!" << endl;
return ;
}
// 初始化"顶点"
for (i = 0; i < mVexNum; i++)
{
cout << "vertex(" << i << "): ";
mVexs[i] = readChar();
}
// 初始化"边"
for (i = 0; i < mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
cout << "edge(" << i << "): ";
c1 = readChar();
c2 = readChar();
p1 = getPosition(c1);
p2 = getPosition(c2);
if (p1==-1 || p2==-1)
{
cout << "input error: invalid edge!" << endl;
return ;
}
mMatrix[p1][p2] = 1;
mMatrix[p2][p1] = 1;
}
}
/*
* 创建图(用已提供的矩阵)
*
* 参数说明：
* vexs -- 顶点数组
* vlen -- 顶点数组的长度
* edges -- 边数组
* elen -- 边数组的长度
*/
MatrixUDG::MatrixUDG(char vexs[], int vlen, char edges[][2], int elen)
{
int i, p1, p2;
// 初始化"顶点数"和"边数"
mVexNum = vlen;
mEdgNum = elen;
// 初始化"顶点"
for (i = 0; i < mVexNum; i++)
mVexs[i] = vexs[i];
// 初始化"边"
for (i = 0; i < mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
p1 = getPosition(edges[i][0]);
p2 = getPosition(edges[i][1]);
mMatrix[p1][p2] = 1;
mMatrix[p2][p1] = 1;
}
}
/*
* 析构函数
*/
MatrixUDG::~MatrixUDG()
{
}
/*
* 返回ch在mMatrix矩阵中的位置
*/
int MatrixUDG::getPosition(char ch)
{
int i;
for(i=0; i<mVexNum; i++)
if(mVexs[i]==ch)
return i;
return -1;
}
/*
* 读取一个输入字符
*/
char MatrixUDG::readChar()
{
char ch;
do {
cin >> ch;
} while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
return ch;
}
/*
* 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*/
int MatrixUDG::firstVertex(int v)
{
int i;
if (v<0 || v>(mVexNum-1))
return -1;
for (i = 0; i < mVexNum; i++)
if (mMatrix[v][i] == 1)
return i;
return -1;
}
/*
* 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*/
int MatrixUDG::nextVertex(int v, int w)
{
int i;
if (v<0 || v>(mVexNum-1) || w<0 || w>(mVexNum-1))
return -1;
for (i = w + 1; i < mVexNum; i++)
if (mMatrix[v][i] == 1)
return i;
return -1;
}
/*
* 深度优先搜索遍历图的递归实现
*/
void MatrixUDG::DFS(int i, int *visited)
{
int w;
visited[i] = 1;
cout << mVexs[i] << " ";
// 遍历该顶点的所有邻接顶点。若是没有访问过，那么继续往下走
for (w = firstVertex(i); w >= 0; w = nextVertex(i, w))
{
if (!visited[w])
DFS(w, visited);
}
}
/*
* 深度优先搜索遍历图
*/
void MatrixUDG::DFS()
{
int i;
int visited[MAX]; // 顶点访问标记
// 初始化所有顶点都没有被访问
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "DFS: ";
for (i = 0; i < mVexNum; i++)
{
//printf("\n== LOOP(%d)\n", i);
if (!visited[i])
DFS(i, visited);
}
cout << endl;
}
/*
* 广度优先搜索（类似于树的层次遍历）
*/
void MatrixUDG::BFS()
{
int head = 0;
int rear = 0;
int queue[MAX]; // 辅组队列
int visited[MAX]; // 顶点访问标记
int i, j, k;
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "BFS: ";
for (i = 0; i < mVexNum; i++)
{
if (!visited[i])
{
visited[i] = 1;
cout << mVexs[i] << " ";
queue[rear++] = i; // 入队列
}
while (head != rear)
{
j = queue[head++]; // 出队列
for (k = firstVertex(j); k >= 0; k = nextVertex(j, k)) //k是为访问的邻接顶点
{
if (!visited[k])
{
visited[k] = 1;
cout << mVexs[k] << " ";
queue[rear++] = k;
}
}
}
}
cout << endl;
}
/*
* 打印矩阵队列图
*/
void MatrixUDG::print()
{
int i,j;
cout << "Martix Graph:" << endl;
for (i = 0; i < mVexNum; i++)
{
for (j = 0; j < mVexNum; j++)
cout << mMatrix[i][j] << " ";
cout << endl;
}
}
int main()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'F', 'G'}};
int vlen = sizeof(vexs)/sizeof(vexs[0]);
int elen = sizeof(edges)/sizeof(edges[0]);
MatrixUDG* pG;
// 自定义"图"(输入矩阵队列)
//pG = new MatrixUDG();
// 采用已有的"图"
pG = new MatrixUDG(vexs, vlen, edges, elen);
pG->print(); // 打印图
pG->DFS(); // 深度优先遍历
pG->BFS(); // 广度优先遍历
return 0;
}邻接表实现无向图的BFS与DFS
/**
* C++: 邻接表表示的"无向图(List Undirected Graph)"
*
* @author skywang
* @date 2014/04/19
*/
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
#define MAX 100
// 邻接表
class ListUDG
{
private: // 内部类
// 邻接表中表对应的链表的顶点
class ENode
{
public:
int ivex; // 该边所指向的顶点的位置
ENode *nextEdge; // 指向下一条弧的指针
};
// 邻接表中表的顶点
class VNode
{
public:
char data; // 顶点信息
ENode *firstEdge; // 指向第一条依附该顶点的弧
};
private: // 私有成员
int mVexNum; // 图的顶点的数目
int mEdgNum; // 图的边的数目
VNode mVexs[MAX];
public:
// 创建邻接表对应的图(自己输入)
ListUDG();
// 创建邻接表对应的图(用已提供的数据)
ListUDG(char vexs[], int vlen, char edges[][2], int elen);
~ListUDG();
// 深度优先搜索遍历图
void DFS();
// 广度优先搜索（类似于树的层次遍历）
void BFS();
// 打印邻接表图
void print();
private:
// 读取一个输入字符
char readChar();
// 返回ch的位置
int getPosition(char ch);
// 深度优先搜索遍历图的递归实现
void DFS(int i, int *visited);
// 将node节点链接到list的最后
void linkLast(ENode *list, ENode *node);
};
/*
* 创建邻接表对应的图(自己输入)
*/
ListUDG::ListUDG()
{
char c1, c2;
int v, e;
int i, p1, p2;
ENode *node1, *node2;
// 输入"顶点数"和"边数"
cout << "input vertex number: ";
cin >> mVexNum;
cout << "input edge number: ";
cin >> mEdgNum;
if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1))))
{
cout << "input error: invalid parameters!" << endl;
return ;
}
// 初始化"邻接表"的顶点
for(i=0; i<mVexNum; i++)
{
cout << "vertex(" << i << "): ";
mVexs[i].data = readChar();
mVexs[i].firstEdge = NULL;
}
// 初始化"邻接表"的边
for(i=0; i<mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
cout << "edge(" << i << "): ";
c1 = readChar();
c2 = readChar();
p1 = getPosition(c1);
p2 = getPosition(c2);
// 初始化node1
node1 = new ENode();
node1->ivex = p2;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == NULL)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
node2 = new ENode();
node2->ivex = p1;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == NULL)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 创建邻接表对应的图(用已提供的数据)
*/
ListUDG::ListUDG(char vexs[], int vlen, char edges[][2], int elen)
{
char c1, c2;
int i, p1, p2;
ENode *node1, *node2;
// 初始化"顶点数"和"边数"
mVexNum = vlen;
mEdgNum = elen;
// 初始化"邻接表"的顶点
for(i=0; i<mVexNum; i++)
{
mVexs[i].data = vexs[i];
mVexs[i].firstEdge = NULL;
}
// 初始化"邻接表"的边
for(i=0; i<mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
c1 = edges[i][0];
c2 = edges[i][1];
p1 = getPosition(c1);
p2 = getPosition(c2);
// 初始化node1
node1 = new ENode();
node1->ivex = p2;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == NULL)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
node2 = new ENode();
node2->ivex = p1;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == NULL)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 析构函数
*/
ListUDG::~ListUDG()
{
}
/*
* 将node节点链接到list的最后
*/
void ListUDG::linkLast(ENode *list, ENode *node)
{
ENode *p = list;
while(p->nextEdge)
p = p->nextEdge;
p->nextEdge = node;
}
/*
* 返回ch的位置
*/
int ListUDG::getPosition(char ch)
{
int i;
for(i=0; i<mVexNum; i++)
if(mVexs[i].data==ch)
return i;
return -1;
}
/*
* 读取一个输入字符
*/
char ListUDG::readChar()
{
char ch;
do {
cin >> ch;
} while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
return ch;
}
/*
* 深度优先搜索遍历图的递归实现
*/
void ListUDG::DFS(int i, int *visited)
{
ENode *node;
visited[i] = 1;
cout << mVexs[i].data << " ";
node = mVexs[i].firstEdge;
while (node != NULL)
{
if (!visited[node->ivex])
DFS(node->ivex, visited);
node = node->nextEdge;
}
}
/*
* 深度优先搜索遍历图
*/
void ListUDG::DFS()
{
int i;
int visited[MAX]; // 顶点访问标记
// 初始化所有顶点都没有被访问
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "DFS: ";
for (i = 0; i < mVexNum; i++)
{
if (!visited[i])
DFS(i, visited);
}
cout << endl;
}
/*
* 广度优先搜索（类似于树的层次遍历）
*/
void ListUDG::BFS()
{
int head = 0;
int rear = 0;
int queue[MAX]; // 辅组队列
int visited[MAX]; // 顶点访问标记
int i, j, k;
ENode *node;
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "BFS: ";
for (i = 0; i < mVexNum; i++)
{
if (!visited[i])
{
visited[i] = 1;
cout << mVexs[i].data << " ";
queue[rear++] = i; // 入队列
}
while (head != rear)
{
j = queue[head++]; // 出队列
node = mVexs[j].firstEdge;
while (node != NULL)
{
k = node->ivex;
if (!visited[k])
{
visited[k] = 1;
cout << mVexs[k].data << " ";
queue[rear++] = k;
}
node = node->nextEdge;
}
}
}
cout << endl;
}
/*
* 打印邻接表图
*/
void ListUDG::print()
{
int i,j;
ENode *node;
cout << "List Graph:" << endl;
for (i = 0; i < mVexNum; i++)
{
cout << i << "(" << mVexs[i].data << "): ";
node = mVexs[i].firstEdge;
while (node != NULL)
{
cout << node->ivex << "(" << mVexs[node->ivex].data << ") ";
node = node->nextEdge;
}
cout << endl;
}
}
int main()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'F', 'G'}};
int vlen = sizeof(vexs)/sizeof(vexs[0]);
int elen = sizeof(edges)/sizeof(edges[0]);
ListUDG* pG;
// 自定义"图"(输入矩阵队列)
//pG = new ListUDG();
// 采用已有的"图"
pG = new ListUDG(vexs, vlen, edges, elen);
pG->print(); // 打印图
pG->DFS(); // 深度优先遍历
pG->BFS(); // 广度优先遍历
return 0;
}References
数据结构之DFS与BFS实现的更多相关文章
- 数据结构之DFS与BFS
深度搜索(DFS) and 广度搜索(BFS) 代码如下: #include "stdafx.h" #include<iostream> #include<st ...
- 【数据结构与算法笔记04】对图搜索策略的一些思考（包括DFS和BFS）
图搜索策略 这里的"图搜索策略"应该怎么理解呢? 首先,是"图搜索",所谓图无非就是由节点和边组成的,那么图搜索也就是将这个图中所有的节点和边都访问一遍. 其次 ...
- 数据结构(12) -- 图的邻接矩阵的DFS和BFS
//////////////////////////////////////////////////////// //图的邻接矩阵的DFS和BFS ////////////////////////// ...
- 数据结构(11) -- 邻接表存储图的DFS和BFS
/////////////////////////////////////////////////////////////// //图的邻接表表示法以及DFS和BFS //////////////// ...
- 数据结构基础(21) --DFS与BFS
DFS 从图中某个顶点V0 出发,访问此顶点,然后依次从V0的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和V0有路径相通的顶点都被访问到(使用堆栈). //使用邻接矩阵存储的无向图的深度 ...
- 《数据结构》C++代码 BFS与DFS
BFS,广度优先搜索,一层一层去遍历图,故称广度优先.实现方式:队列. DFS,深度优先搜索,撞墙才回头的遍历,称为深度优先.实现方式:递归(栈). 这两种遍历方式,是访问图的基本方式.如果拿树做对比 ...
- 列出连通集（DFS及BFS遍历图） -- 数据结构
题目: 7-1 列出连通集 (30 分) 给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集.假设顶点从0到N−1编号.进行搜索时,假设我们总是从编号最小的顶点出发,按编号递 ...
- Java数据结构——图的DFS和BFS
1.图的DFS: 即Breadth First Search,深度优先搜索是从起始顶点开始,递归访问其所有邻近节点,比如A节点是其第一个邻近节点,而B节点又是A的一个邻近节点,则DFS访问A节点后再访 ...
- 图论中DFS与BFS的区别、用法、详解…
DFS与BFS的区别.用法.详解? 写在最前的三点: 1.所谓图的遍历就是按照某种次序访问图的每一顶点一次仅且一次. 2.实现bfs和dfs都需要解决的一个问题就是如何存储图.一般有两种方法:邻接矩阵 ...
随机推荐
- Android 软键盘盖住输入框的问题
当在Android的layout设计里面如果输入框过多,则在输入弹出软键盘的时候,下面的输入框会有一部分被软件盘挡住,从而不能获取焦点输入. 解决办法: 方法一:在你的activity中的oncrea ...
- BZOJ1500——维修序列
动态的最大子段和 就是splay啊,说一下GSS1吧,维护四个值,一个是这个区间和(下面说sum), 一个是从左边开始的最大和(下面说ls)和右边开始的最大和(下面说rs), 还有一个就是最大区间和( ...
- 常用的Git Tips
导读 Git被越来越多的公司使用,因此我们需要了解Git使用过程中的一些技巧. 一.Configuration:配置 列举所有的别名与配置 git config --list Git 别名配置 git ...
- am335x 1G nand 启动Linux qt
针对DRAM的升级,修改u-boot 的参数即可. include/configs/ok335x.h 修改PHYS_DRAM_1_SIZE 为0x40000000 这是1G的大小. 原来512M 为 ...
- 装b指南
提溜一个糖水黄桃罐头瓶,放在桌边,坐下以后,脖子略微后仰,翘着二郎腿,低头盯着屏幕看需求. 最好点一根烟,牌子无所谓,能冒烟就行.要得就是云山雾绕的感觉,从烟雾中眯着眼睛看出去,一副胸有成竹的样. 一 ...
- linux awk, xargs
awk , 很赞的教程:http://coolshell.cn/articles/9070.html xargs, http://blog.csdn.net/andy572633/article/de ...
- 将 JAR 转为 EXE – EXE4J 的使用教程（第一期）（转载）
http://www.iteknical.com/convert-jar-to-exe-phase-i-exe4j-tutorial/
- bootstrap按钮
按钮 基类 -btn 样式 btn-default(默认) btn-link(链接) 大小 btn-*[lg,sm,xs] 状态 active disabled <!DOCTYPE HTML&g ...
- HTML 返回顶部的样式
.fhdb{ width:50px; height:50px; position:fixed; //可以用来定义元素的固定定位. right:20px; //距离右侧20像素 botto ...
- STL---总结
文章转自:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/22/2603525.html 一.STL的六大组件 容器(Container),是一种 ...