Linear Algebra lecture4 note
Inverse of AB,A^(A的转置）
Product of elimination matrices A=LU (no row exchanges)
Inverse of AB,A^(A的转置）:
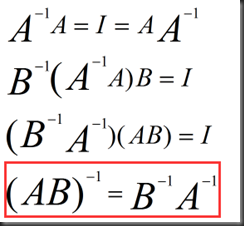
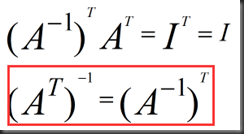
Product of elimination matrices A=LU (no row exchanges)
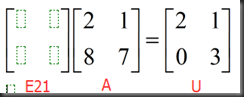
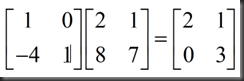
E32E31E21A=U (no row exchanges) EA=U
A=E21`E31`E32`U
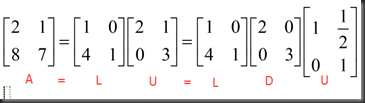
L表示下三角矩阵，lower triangle
D表示对角矩阵，diagonal triangle
A=LU
L=E21`E31`E32`
对比EA=U & A=LU，哪种形式更好一些？
example：
设E31为单位矩阵，
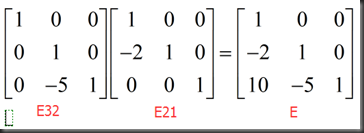
A=LU的形式更加简洁一些，if no row exchanges, multipliers go directly into L
思考：How many operations on n * n Matrix(A)? 也就是多少数字改变了？
假设n=100，
row1 不改变，后续行消元，99*100次运算，约看作100*100次；
对第二行进行消元，98*99次运算，约看作99*99次；
继续…
所以总运算次数为
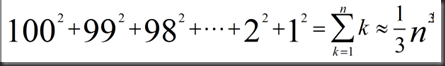
从积分角度考虑可得最终结果
若再考虑等式右侧的b，需要的运算量为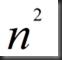
Permutation
考虑单位矩阵的行变换，所有情况一一列出（共6种）
这6个矩阵好像构成了一个群，不论是乘还是逆运算，所得结果均在此群中，且满足条件
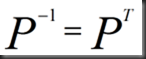
若是4维矩阵，则满足条件的、构成群的矩阵有4！=24个
若是n维矩阵，则满足条件的、构成群的矩阵有n！个
Linear Algebra lecture4 note的更多相关文章
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- Linear Algebra lecture9 note
Linear independence Spanning a space Basis and dimension 以上概念都是针对a bunch of vectors, 不是矩阵里的概念 Supp ...
- Linear Algebra lecture10 note
Four fundamental subspaces( for matrix A) if A is m by n matrix: Column space C(A) in Rm (列空间在m维实 ...
- Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn) rank r r=m solutions exist r=n solutions unique example: 若想方程有解 ...
- Linear Algebra lecture7 note
Computing the nullspace (Ax=0) Pivot variables-free variables Special solutions: rref( A)=R rank o ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture3 note
Matrix multiplication(4 ways!) Inverse of A Gauss-Jordan / find inverse of A Matrix multiplication ...
- Codeforces Gym101502 B.Linear Algebra Test-STL(map)
B. Linear Algebra Test time limit per test 3.0 s memory limit per test 256 MB input standard input ...
随机推荐
- Html标签第三课
1.css div { position:absolute; } #d1 { height:100px; width:100px; border: solid 1px red; background- ...
- WebAPI返回数据类型解惑[转]
最近开始使用WebAPI,上手很容易,然后有些疑惑 1.WebAPI默认返回什么数据类型,json还是xml? 2.怎么修改WebAPI的返回数据类型,我用IE浏览器请求返回的数据都是JSON格式的, ...
- ueditor 图片上传功能（.net）
假如下载的net文件 所在工程引用bin文件中的Newtonsoft.Json.dll 在浏览器中运行 `net/controller.ashx`,如果返回 "`{"state&q ...
- Power of Four（Difficulty: Easy）
题目: Given an integer (signed 32 bits), write a function to check whether it is a power of 4. Example ...
- Activity 生命周期
Activity 的四种基本状态 1.运行态(Running) Activity 处于屏幕最前端,用户可见且获得焦点. 2.暂停态(Paused) Activity被置于后台,用户可见,但失去焦点 3 ...
- 采用ubuntu系统来安装tensorflow
最近在学习google新开源的深度学习框架tensorflow.发现安装它的时候,需要依赖python2.7.X;我之前一直使用的linux是centos.而centos不更新了,里面的自带的pyth ...
- 通过声明Attribute属性改变不同类的输出效果
ConsoleApplication--控制台应用程序 首先创建基类: using System; using System.Collections.Generic; using System.Lin ...
- lucene5学习 - 索引基本操作（创建，查询，更新，删除，分页）
package lucene5; import java.io.IOException; import java.nio.file.Paths; import java.text.SimpleDate ...
- python简易爬虫来实现自动图片下载
菜鸟新人刚刚入住博客园,先发个之前写的简易爬虫的实现吧,水平有限请轻喷. 估计利用python实现爬虫的程序网上已经有太多了,不过新人用来练手学习python确实是个不错的选择.本人借鉴网上的部分实现 ...
- H3C汇聚层交换机认证在线人数展示系统之需求说明和功能点说明
一.需求 (一)每五分钟查询一次交换机的连接情况: (二)每2.5分钟更新每栋楼的连接情况. 二.功能点 序号 功能点说明 待定 完成 未完成 完成时间 预计用时(min) 实际用时(min) 备注 ...