【莫比乌斯反演】关于Mobius反演与gcd的一些关系与问题简化(bzoj 2301 Problem b&&bzoj 2820 YY的GCD&&BZOJ 3529 数表)

---

　　首先我们来看一道题

　  BZOJ 2301 Problem b

---

Description

　　对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

　　第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

　　共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

　　2

　　2 5 1 5 1

　　1 5 1 5 2

Sample Output

　　14

　　3

HINT

　　100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000。

---

　　乍一看，大家的force想法:枚举x，y！之后辗转相除！！

　　但是复杂度已经爆炸。几乎是一个O(n^3)规模的算法

　　

　　继续想！

　　我们发现:为什么要枚举所有的k啊，我们只要把k的倍数枚举一下就行了啊，然后看看两个数除以k后gcd等不等于1就行了啊。

　　这样O(n^2logn)的时间复杂度!

　　继续想！

　　我们求的是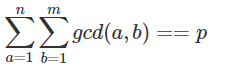

　　我们把它变换一下。。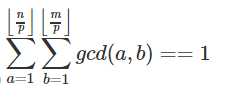

　　而在学习莫比乌斯反演的时候，我们得出了一个性质。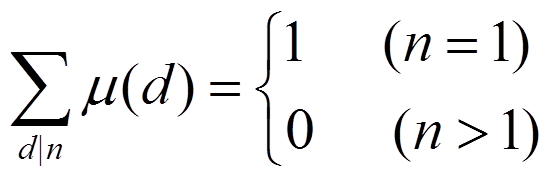

　　所以，我们把gcd(a,b)==1换成上面一行的sigma，把n改成gcd(a,b)即可。

　　变成了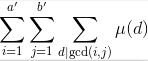

　　现在我们把第三重sigma移动到最外面。变成了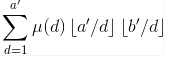(这一步需要仔细思考，要配合容斥原理)

　　复杂度为O(n^2)。然而还是有点慢。

　　

　　我们发现，有一些区间的一些段的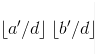是重复的，如下图。

　　

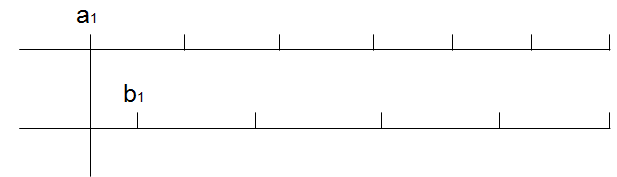
　　a₁的意思是第一个使n/a_i为整数的d。其他同理。

　　在（a₁-1）之前的区间，我们发现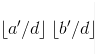一直是重复的，所以我们在线性筛里面放一个处理求Mobius函数的前缀和，最后把一些重复的直接用前缀和乘即可即可，这样节省了很多重复操作。

　　达到了O(nlogn)。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define viper 50005

using namespace std;

bool is_prime[viper];

int prime[viper],size=,mu[viper],sum[viper];

void mu_choice()
{
    mu[]=;
    for(int i=;i<=;i++)
    {
        if(!is_prime[i])prime[++size]=i,mu[i]=-;
        int j=,t=prime[j]*i;
        while(j<=size&&t<=)
        {
            is_prime[t]=;
            if(i%prime[j]==)
            {
                mu[t]=;
                break;
            }
            else mu[t]=-mu[i];
            t=prime[++j]*i;
        }
    }
    for(int i=;i<=;i++)sum[i]=sum[i-]+mu[i];
}

int puck(int l,int r)
{
    if(l<r)swap(l,r);
    int last,re=;
    for(int i=;i<=r;i=last+)
    {
        last=min(l/(l/i),r/(r/i));//每个重复区间的尾端
        re+=(sum[last]-sum[i-])*(l/i)*(r/i);
    }
    return re;
}

int main()
{
    int T,a,b,c,d,k;
    mu_choice();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        a--,c--;
        a/=k,b/=k,c/=k,d/=k;
        printf("%d\n",puck(b,d)+puck(a,c)-puck(a,d)-puck(c,b));//容斥原理
    }
        return ;
}   

　　接下来我们来看下一题。。

　　BZOJ 2820 YY的GCD

---

Description

　　神犇YY虐完数论后给傻×kAc出了一题

　　给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对

　　kAc这种傻×必然不会了，于是向你来请教……

　　多组输入

Input

　　第一行一个整数T 表述数据组数

　　接下来T行，每行两个正整数，表示N, M

Output

　　T行，每行一个整数表示第i组数据的结果

Sample Input

　　2
　　10 10
　　100 100

Sample Output

　　30
　　2791

HINT

　　T = 10000
　　N, M <= 10000000

---

　　乍一看，这不和上题没什么区别啊。。不就是枚举质数然后随便求吗。。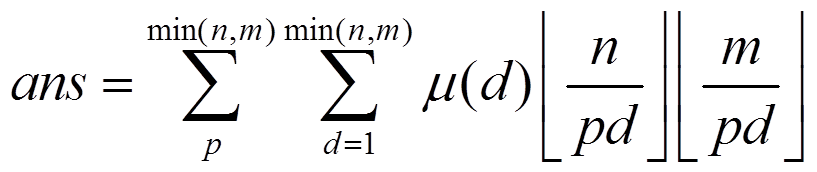

　　然而，这样求肯定TLE。。

　　让我们继续。

　　设T=pd，来变换一下。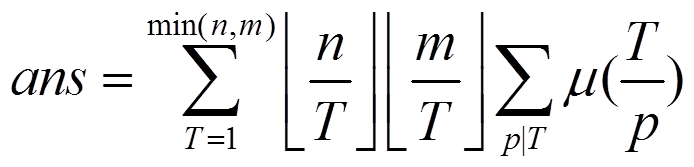

　　之后?把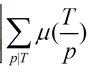预处理一下，把每个质数的倍数枚举一下，分块。。O（n）的时间复杂度(每个质数logn，n内一共n/logn个质数)。

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>

 #define N 10000001

 using namespace std;

 int mu[N],prime[N],b=;
 long long f[N];

 bool is_prime[N];

 void get_mu()
 {
     mu[]=;
     for(int i=;i<=N-;i++)
     {
         if(!is_prime[i])prime[++b]=i,mu[i]=-;
         int j=,t=*i;
         while(j<=b&&t<=N-)
         {
             is_prime[t]=;
             if(i%prime[j]==)
             {
                 mu[t]=;
                 break;
             }
             mu[t]=-mu[i];
             t=prime[++j]*i;
         }
     }
     for(int i=;i<=b;i++)
     {
         int p=prime[i];
         for(int j=;j*p<=N-;j++)
             f[p*j]+=mu[j];
     }
     for(int i=;i<=N-;i++)f[i]+=f[i-];
 }

 int main()
 {
     get_mu();
     int T,l,r;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&l,&r);
         if(l<r)swap(l,r);
         int last;
         long long ans=;
         for(int i=;i<=r;i=+last)
         {
             last=min(l/(l/i),r/(r/i));
             ans+=(long long)(f[last]-f[i-])*(l/i)*(r/i);
         }
         printf("%lld\n",ans);
     }
     return ;
 }

---

　　BZOJ 3529 数表

---

　　

　

Description

有一张N×m的数表，其第i行第j列（1 < =i < =n，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

对每组数据，输出一行一个整数，表示答案模2^31的值。

---

　　让我们先把这道题看简单一点(去掉a的限制)

　　求得是：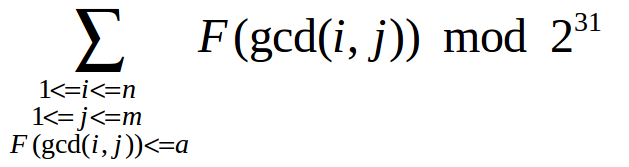

　　F(i)代表i的约数和。

　　

　　令g(i)为1<=x<=n,1<=y<=m,gcd(x,y)=i的数对(x,y)的个数

　　则有。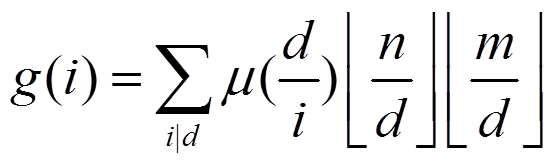

　　

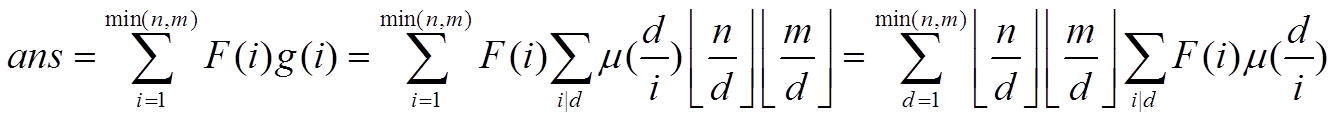
　　接下来又是喜闻乐见的前缀和。

　　在线性筛里面完成即可。

　　但是有a的限制，怎么办？

　　我们可以以a为关键字按升序排序，把F[i]按升序排序。

　　之后每次把a以内的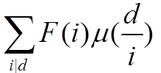按F[i]添加到一个树状数组里面，之后每次分块即可。。

　　

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>

 #define maxq 40001

 #define maxn 100001

 using namespace std;

 struct ed{
     int a,n,m,id,ans;
 }a[maxq];

 bool is_prime[maxn];

 int prime[maxn],b=,mu[maxn],bit[maxn],ans[maxn];

 struct sb{
     int num,Id;
 }f[maxn];

 void mu_choice()
 {
     mu[]=;
     for(int i=;i<=maxn-;i++)
     {
         if(!is_prime[i])prime[++b]=i,mu[i]=-;
         int j=,t=*i;
         while(j<=b&&t<=maxn-)
         {
             is_prime[t]=;
             if(i%prime[j]==)
             {
                 mu[t]=;
                 break;
             }
             mu[t]=-mu[i];
             t=prime[++j]*i;
         }
     }
     for(int i=;i<maxn;i++)
     {
         for(int j=;j*i<maxn;j++)
             f[j*i].num+=i;
         f[i].Id=i;
     }
 }

 bool cmp(const ed A,const ed B)
 {
     return A.a<B.a;
 }

 bool cmp2(const sb A,const sb B)
 {
     return A.num<B.num;
 }

 void add(int pos,int num)
 {
     while(pos<=maxn-)
     {
         bit[pos]+=num;
         pos+=pos&-pos;
     }
 }

 int sum(int pos)
 {
     int ne=;
     while(pos>)
     {
         ne+=bit[pos];
         pos-=pos&-pos;
     }
     return ne;
 }

 void solve(int x)
 {
     int last;
     for(int i=;i<=a[x].n;i=last+)
     {
         last=min(a[x].n/(a[x].n/i),a[x].m/(a[x].m/i));
         ans[a[x].id]+=(sum(last)-sum(i-))*(a[x].n/i)*(a[x].m/i);
     }
 }

 int main()
 {
     #ifndef ONLINE_JUDGE
            freopen("3529.in","r",stdin);
           freopen("3529.out","w",stdout);
     #endif
     int T,aa,n,m;
     scanf("%d",&T);
     for(int i=;i<=T;i++)
     {
         scanf("%d%d%d",&n,&m,&aa);
         if(n>m)swap(n,m);
         a[i].a=aa,a[i].n=n,a[i].m=m,a[i].id=i;
     }
     mu_choice();
     sort(+a,a++T,cmp);
     sort(+f,f+maxn,cmp2);
     int puck=;
     for(int i=;i<=T;i++)
     {
         while(puck<maxn&&f[puck].num<=a[i].a)
         {
             for(int j=;j<=((maxn-)/f[puck].Id);j++)
                 add(j*f[puck].Id,mu[j]*f[puck].num);
             puck++;
         }
         solve(i);
     }
     for(int i=;i<=T;i++)
         printf("%d\n",ans[i]&0x7fffffff);
     return ;
 }

　　代码凑合着看吧。。