现代3D图形编程学习-基础简介(1) (译)

本书系列

现代3D图形编程学习

基础简介

并不像本书的其他章节，这章内容没有相关的源代码或是项目。本章，我们将讨论向量，图形渲染理论，以及OpenGL。

向量

在阅读这本书的时候，你需要熟悉代数和几何知识，但对于向量的理解并不是必要的。因为，在接下去的内容中，会对向量的基本概念作出介绍。

在面对几何或是数值相关的内容时，向量可以有很多不同的解释。在任何一种情况，向量是具有维度的。二维的向量限制在一个平面上，然而三维的向量可以在任何的物理空间。向量还可以有更高的维度，但是通常情况下，我们处理的向量的维度只在二维到四维之间。

严格的来说，向量还可以存在仅仅一维的情况。这样的向量被称为标量。

在几何术语中，向量可以表示两个概念：一个空间中的位置或是一个方向。

向量的位置表示空间中一个特殊的位置。如，在下图中我们有一个向量位置A。

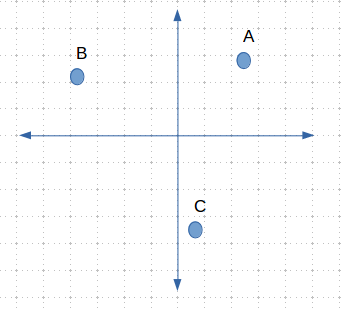Figure1 vector position

向量也可以表示为方向。方向向量没有一个原点；只用来表示空间中的方向。下图中给出了不同的方向向量，其中B和D虽然画在不同的位置，但它们是相同的方向向量。

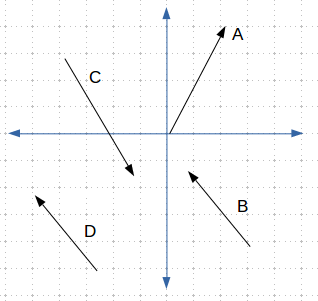Figure2 Direction Vectors

对于几何而言，以上的表达方式已经够用了，但是向量还可以被解释成数值。这时候，一个向量表示为一个数字序列，没一个数字表示一个维度。因此，二维的向量有两个数字；三维的向量有三个数字。对于四维向量也是一样的。从数字上来说，标量仅仅是一个数字。

向量中的没一个数字都被称为要素（component）。每一个要素都有自己的名字。对于我们而言，向量的第一个要素被成为X，第二个被成为Y，第三个是Z，第四个是W。

当用文本的方式来书写向量的时候，它们通常被括号包围。因此，一个3D向量可以是(0,2,4)，其中X为0,Y为2,Z为4.当他们以公式的形式进行书写的时候，表现形式为：

\[
\vec {a} = \left[
\begin{matrix}
1 \\
2 \\
3
\end{matrix}
\right]
\]

在数学公式中，向量变量会以粗体或是上面带箭头的形式出现。

当在绘制向量的时候，需要区分位置向量和方向向量。但是，它们两者的数值并没有区别。唯一的区别是你怎么使用它们，而不是怎么用数字表达它们。因此，你可以把一个点考虑成一个向量，然后执行一些操作，最后再将它考虑成一个点。

虽然向量的各个成分之间是独立的，但是数学公式操作它们的时候，它们是一个整体。在接下来的内容中，我们会通过几何和数值的方式展示一些操作。

向量加法 你可以对两个向量执行加法操作。从图形上看是这样的：

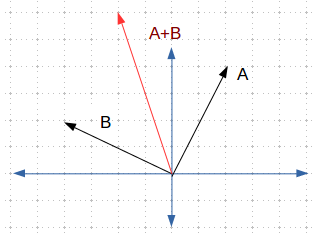Figure3 Vector Addition

要记得的是，方向向量在不改变具体数值的情况下，可以对其进行移动。因此，如果你将两个向量放置为首位相接，向量的加法可以简单的表示成从第一个向量的尾部指向第二个向量的头。

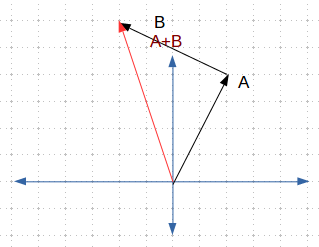Figure4 Vector Addition Head-to-Tail

从数值上来讲，两个向量的求和就是将两个向量的各个成分相加，

公式1. 向量相加
\[
\vec{a} + \vec{b} = \left[ \begin{matrix} a_x \\ a_y \\ a_z \end{matrix} \right] + \left[ \begin{matrix} b_x \\ b_y \\ b_z \end{matrix} \right] = \left[ \begin{matrix} a_x+b_x \\ a_y+b_y \\ a_z+b_z \end{matrix} \right]
\]

一个操作需要对向量各个成分进行，被称为分量操作（component-wise operation）。向量加法就是一个分量操作。任何一个分量操作都需要保证两个向量有相同的维度。

向量求反和减法 你可以对一个向量去反，就是逆转一个向量的方向。

Figure5 Vector Negation

从数值上来看，就是对向量中的每个成分都去反。

公式2. 向量去反

\[-\vec{a}=-\left[\begin{matrix}a_x \\ a_y \\ a_z \end{matrix} \right]=\left[\begin{matrix} -a_x \\ -a_y \\ -a_z \end{matrix} \right]\]

正如数值运算，向量的减法就是一个向量和第二个向量的反进行相加。

Figure6 Vector Subtraction

向量乘法 向量乘法操作是向量操作中为数不多的没有几何概念与之对应的操作。将两个方向或是两个位置进行相乘，并没有什么意义。但这并不是说向量的乘法没有作用。

数值上，向量的乘法，就是将对应的各个成分相乘。

公式3. 向量乘法

\[ \vec{a}*\vec{b}=\left[\begin{matrix} a_x \\ a_y \\ a_z \end{matrix}\right]*\left[\begin{matrix}b_x \\ b_y \\ b_z \end{matrix}\right]=\left[\begin{matrix} a_x*b_x \\ a_y*b_y \\ a_z*b_z \end{matrix}\right]\]

向量缩放操作 向量可以乘以一个标量。这个标量仅仅是一个数值。更具这个标量的值，这个向量可能被放大或缩小。

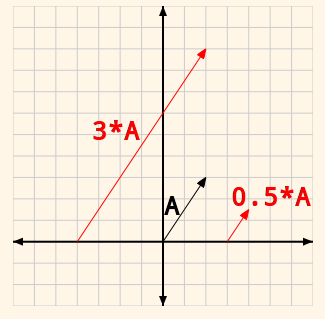Figure7 Vector Scaling

数值运算上，就是将向量的各个成分和标量进行相乘。

公式4. 向量缩放操作

\[ s*\vec{a}=a*\left[\begin{matrix} a_x \\ a_y \\ a_z\end{matrix}\right]=\left[\begin{matrix} s*a_x \\ s*a_y \\ s*a_z \end{matrix}\right] \]

标量也可以和向量相加，这同样没有什么几何意义。公式如下：

公式5. 向量标量相加

\[s+\vec{a}=s+\left[\begin{matrix} a_x \\ a_y \\ a_z\end{matrix}\right]=\left[\begin{matrix}s+a_x \\ s+a_y \\ s+a_z \end{matrix}\right]\]

向量代数 理解这些向量操作之间的关系是有帮助的。

向量加法乘法遵循很多和标量加法乘法相同的规则。它们是交换率，结合率，和分配率。

公式6. 向量代数

• 交换率：\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\); \(\vec{a}*\vec{b}=\vec{b}*\vec{a}\)
• 结合率：\(\vec{a}+\left(\vec{b}+\vec{c}\right)=\left(\vec{a}+\vec{b}\right)+\vec{c}\); \(\vec{a}*\left(\vec{b}*\vec{c}\right)=\left(\vec{a}*\vec{b}\right)*\vec{c}\)
• 分配率：\(\vec{a}*\left(\vec{b}+\vec{c}\right)=\left(\vec{a}*\vec{b}\right)+\left(\vec{a}*\vec{c}\right)\)

向量和标量具有类似的特性。

长度. 向量也有长度，表示从起点到终点的距离。

公式7. 向量长度

\[ |\vec{a}|=\sqrt{a_x^2+a_y^2+a_z^2}\]

这里使用了毕达哥拉斯定理来计算向量的长度。这个适用于任何维度的向量，并不单单是二维或三维向量。

单位向量与标准化 一个向量的长度为一，那么这个向量是 单位向量 。在数学公式中单位向量的表示方式是在变量名上面加个^。

一个向量转变成单位向量的过程叫做 标准化 。将向量除以改向量的长度就能够得到它的长度。

公式8. 向量标准化

\[\hat a=\frac{1}{|\vec{a}|}*\vec{a}=\left[\begin{matrix} \frac{a_x}{|\vec{a}|} \\ \frac{a_x}{|\vec{a}|} \\ \frac{a_x}{|\vec{a}|} \end{matrix}\right]\]

这些并不是本书中用到的所有的向量操作。新的向量操作会在它们第一次被使用到的时候进行介绍。并且，并不像这里使用到了公式，它们中的大多数将不是针对各个成分的独立操作。

范围符号 本书中会使用标准的标识来标记一个值的具体范围。

如果一个值在0～1之间，并且可以等于0和1,那么标记为[0, 1]。放括号表示范围包括了相邻的值。

如果一个值在0～1范围，但不包括0,那么标记为(0, 1]。圆括号表示相邻的值并不包括在范围内。

如果一个值表示0和大于0的任何数值，那么标记为\([0, \infty)\)，需要注意的是无穷大是不可达到的，因此它总是被排除在范围之外的。任何一个小于0的范围则标记为\((-\infty,0)\)。