luogu P1310 表达式的值

题目描述

对于1 位二进制变量定义两种运算：

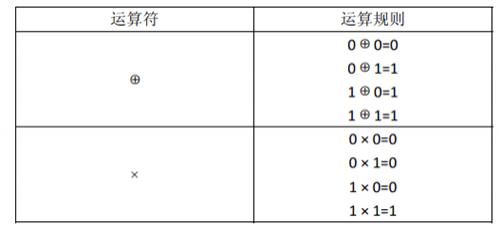
运算的优先级是：

先计算括号内的，再计算括号外的。
“× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如_+(_*_)，请你在横线处填入数字0 或者1 ，请问有多少种填法可以使得表达式的值为0 。

输入输出格式

输入格式：

输入文件名为exp.in ，共 2 行。

第1 行为一个整数 L，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 L 个字符，其中只包含’（’、’）’、’+’、’*’这4 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。

输出格式：

输出文件exp.out 共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对10007 取模后的结果。

输入输出样例

输入样例#1：复制

4

+(*)

输出样例#1：复制

３

说明

【输入输出样例说明】

给定的表达式包括横线字符之后为：_+(_*_)

在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。

【数据范围】

对于20% 的数据有 0 ≤ L ≤ 10。

对于50% 的数据有 0 ≤ L ≤ 1,000。

对于70% 的数据有 0 ≤ L ≤ 10,000 。

对于100%的数据有 0 ≤ L ≤ 100,000。

对于50% 的数据输入表达式中不含括号。

开始写的区间dp....我真是菜

然后借鉴candy大神的blog

笛卡尔树建表达式树，然后树形dp

dp[i][1/0]表示根节点为i的区间值为1/0的方案数

文献http://wenku.baidu.com/link?url=jvyUVTTGFC27LnlHkzQ0OObqeBFDwCYvuCbiHHG5CaPXrjFiGoBtiLhdfNIhW1vHNNZ-Umb_zTKnCOQK3WTw0N8KRQT8m2lfBBMsHpoIChC

                        #include<algorithm>

#include<iostream>

#include<cstring>

#include<cstdio>

#include<cmath>

using namespace std;

const int N=,MOD=;

int n;

char s[N];

struct node{

    int l,r;

    char op;

}tree[N];

int cnt=,w[N],root=;

void build(){

    int p=,cnt=;

    for(int i=;i<=n;i++){

        if(s[i]=='(') p++;if(s[i]==')') p--;

        if(s[i]=='+') {w[++cnt]=p*+;

            tree[cnt].op=s[i];

        }

        if(s[i]=='*') w[++cnt]=p*+,tree[cnt].op=s[i];;

    }

    int st[N],k,top=-;

    for(int i=;i<=cnt;i++) {

        k=top;

        while(k>=&&w[st[k]]>w[i]) k--;

        if(k!=-)tree[st[k]].r=i;

        if(k<top) tree[i].l=st[k+];

        st[++k]=i;

        top=k;

    }

    root=st[];

}

int f[N][];

void dp(int i) {

    if(i==) return;

    if(f[i][]!=) return;

    int l=tree[i].l,r=tree[i].r;char op=tree[i].op;

    dp(l);dp(r);

    if(op=='+'){

        f[i][]=f[l][]*f[r][];

        f[i][]=f[l][]*f[r][]+f[l][]*f[r][]+f[l][]*f[r][];

    }

    if(op=='*'){

        f[i][]=f[l][]*f[r][];

        f[i][]=f[l][]*f[r][]+f[l][]*f[r][]+f[l][]*f[r][];

    }

    f[i][]%=MOD;f[i][]%=MOD;

}

int main() {

    scanf("%d",&n);

    scanf("%s",s+);

    build();

    f[][]=f[][]=;

    dp(root);

    printf("%d",f[root][]%MOD);

    return ;

}