Trie入门讲解

我们常常用Trie（也叫前缀树）来保存字符串集合。如下图所示就是一个Trie。

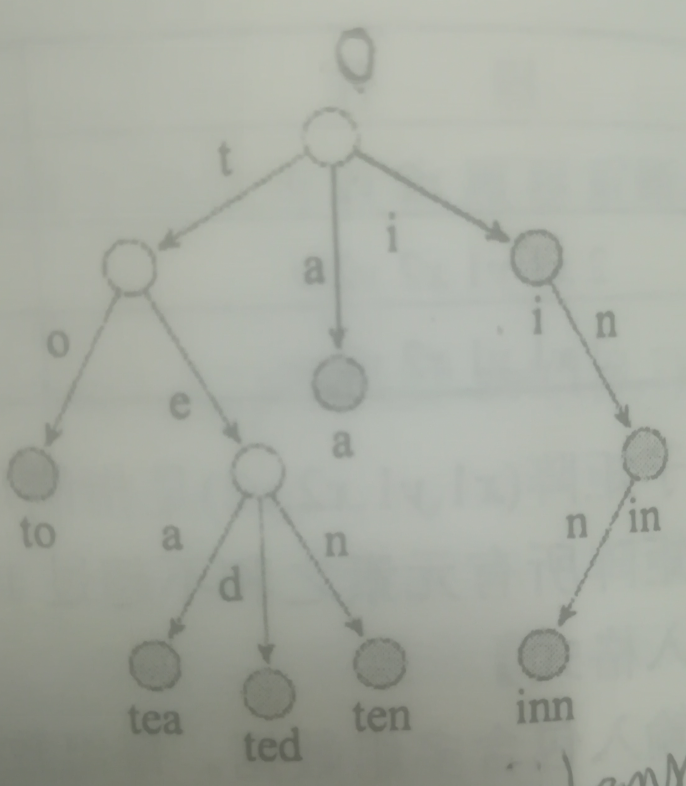
上图表示的字符串集合为$\{a,to,tea,ted,ten,i,in,inn \}$，每个单词的结束位置对应一个“单词结点”。反过来，从根节点到每个单词结点的路径上的所有字母（不是结点上的字母）连接而成的字符串就是该结点对应的字符串。在程序上，将根节点编号为0，然后把其余结点编号为从1开始的正整数，然后用一个数组来保存每个结点的所有子节点，用下标直接存取。

具体来说，可以用$ch[i][j]$保存结点$i$的那个编号为$j$的子结点。为什么叫“编号为$j$呢？”比如，若是处理全部由小写字母组成的字符串，把所有小写字母按照字典序编号为0，1，2，...，则$ch[i][0]$表示结点$i$的子结点$a$。如果这个子结点不存在，则$ch[i][0]=0$。用sigma_size表示字符集的大小，比如，当字符集为全体小写字母时，sigma_szie=26。

使用Trie的时候，往往需要在单词结点上附加信息，其中$val[i]$表示结点$i$对应的附加信息。例如，如果每个字符串有一个权值，就可以把这个权值保存在$val[i]$中。简单起见，下面的额代码假定权值大于0，因此$val[i]>0$当且仅当结点$i$是单词结点（即val为0表示中间结点）。

Trie的定义、插入和查找的代码：

struct Trie
{
    int ch[maxnode][sigma_size];
    int val[maxnode];
    int sz;
    void clear(){ sz = ; memset(ch[], , sizeof(ch[])); }

    int idx(char c) { return c - 'a'; }   //字符c的编号

    //插入字符串s,附加信息为v。注意v必需非0，因为0代表"本结点不是单词结点"
    void insert(const char *s, int v)
    {
        int u = , n = strlen(s);
        for (int i = ; i < n; i++)
        {
            int c = idx(s[i]);
            if (!ch[u][c])
            {
                memset(ch[sz], , sizeof(ch[sz]));
                val[sz] = ;     //中间结点的附加信息为0
                ch[u][c] = sz++;        //新建结点
            }
            u = ch[u][c];      //往下走
        }
        val[u] = v;            //字符串的最后一个字符的附加信息为v
    }

    //找字符串s的长度不超过len的前缀
    void find(const char* s, int len, vector<int>& ans)
    {
        int u = ;
        for (int i = ; i < len; i++)
        {
            if (s[i] == '\0')  break;
            int c = idx(s[i]);
            if (!ch[u][c])  break;
            u = ch[u][c];    //往下走
            if (val[u] != )  ans.push_back(val[u]);   //找到一个前缀
        }
    }
};