校内考试之zay与银临(day1)

T1大美江湖（洛谷P5006）

zayの题解：

这个题的本质是模拟

不过有卡ceil的地方

ceil是对一个double进行向上取整，而对于int/int来说，返回值是int

举个生动的栗子

ceil(5/3)=1  因为5是int，3是int，所以5/3返回1，对1向上取整为1

正确写法：ceil(1.0*5/3)  返回2

直接上AC代码（向上取整手写的）

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int n,m,hpe,ste,dee,x,y,stp,dep,q,sunshi;
char c[][];
int main()
{   freopen("mzq.in","r",stdin);//输入输出文件差点错了要凉
    freopen("mzq.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
       scanf("%s",c[i]+);
    }
    scanf("%d%d%d",&hpe,&ste,&dee);
    scanf("%d%d",&x,&y);
    scanf("%d%d",&stp,&dep);
    scanf("%d",&q);
    for(int i=;i<=q;i++)
    { int cz;
      scanf("%d",&cz);
      if(cz==)
      {printf("%d %d %d\n",sunshi,stp,dep);
      }
      else
      {  int di;
        scanf("%d",&di);
         if(di==)y--;
         if(di==)y++;
         if(di==)x--;
         if(di==)x++;
         if(c[x][y]=='Y')dep+=;
         if(c[x][y]=='Q')stp+=;
         if(c[x][y]=='R'){sunshi-=;if(sunshi<)sunshi=;}
         if(c[x][y]=='M')
         {
         int rqy1=hpe/(max(,stp-dee));
         if(hpe%(max(,stp-dee)))rqy1++;
         int rqy2=max(,ste-dep);
         sunshi+=max(,rqy1*rqy2);
         }
      }
    }
    return ;
}

洛谷中对人物的操作是字符形式，改一下就好了

T2：腐草为萤（洛谷P5007）

刚来完一个大模拟，接下来就是大大的懵逼

这玩意咋整啊？咱也不知道咱也不敢问

zayの题解：

我们来理一理思路

像这种选择数加和最大的问题一般有两种解法

1.DP

2.组合数学

-------------zay

这里我们先讲DP(wz太强了，他用组合数学做的，AC了！！！！！)

我们设fx为以x为根时，当前的答案是fx

我们先想一想二叉树（毕竟数据有特殊情况）

这是个一个孩子都没有的二叉树，此时fx为x的权值

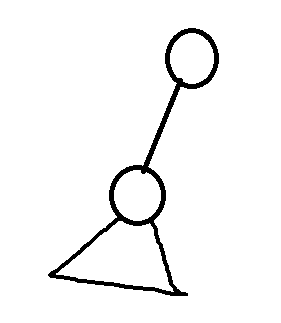
这是个有一个孩子的二叉树（下面的小三角是以x的孩子为根的子树）

对于fx,我们可以选x，不选它儿子和下面的子树，答案为x的权值

我们也可以选它儿子u不选它，答案为fu

综上：fx=fu+x的权值

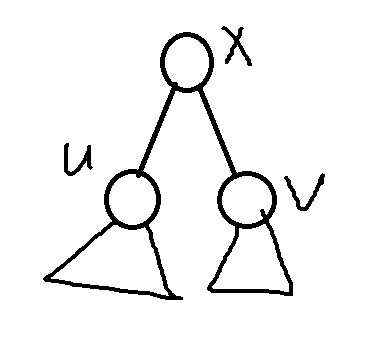
这是一棵有两个儿子的二叉树（三角还是子树）

那么我们肯定可以选u,v,x

再考虑一下u和v能不能进行一番乱搞

显然u的子树里任意一个集合都可以和v进行一番乱搞

那设u子树里的一个集合s的权值是ws,我们再设一个新的变量g,gx为以x为根的子树，所选集合的个数

对于在u子树里的一个集合s,v子树里的任意一个集合与s都能够组成一个新的幼嫩集合

那么u乱搞后对答案的贡献就是Σws*gv，Σws就是fu

同理v乱搞后对答案的贡献就是fv*gu

所以fx=fu+fv+u的权值+fv*gu+fu*gv

那我们再来想一想怎么维护gx

对于没有孩子的点x来说，gx=1(只能和自己搞了qwq)

对于有一个孩子的点x来说，gx=gu(u是x的孩子)+1(可以选u,也可以和自己搞)

对于有两个孩子的点x来说，就有点复杂了

显然可以选u(左孩子），v（右孩子），x（它自己）

再考虑u,v乱搞

对于u子树里的任意一个集合s来说，v子树里的任意一个集合还是都可以和它搞

而u子树里有gu个集合，所以乱搞对gx的贡献是gx*gy

所以gx=gu+gv+1+gu*gv

二叉树讲完了，再考虑不知道多少叉树

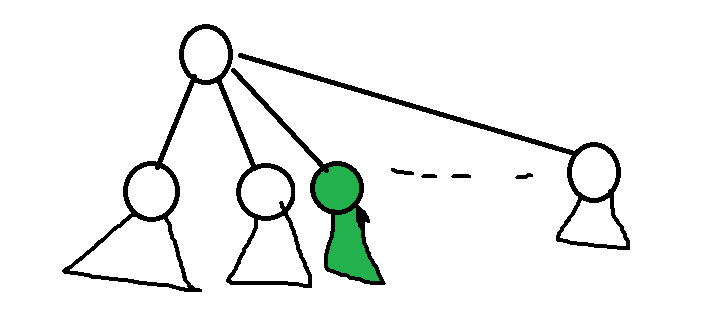
假设我们当前遍历到了绿色的这棵子树，参考搞二叉树的思路，怎么做呢？

我们不妨把这棵树左边的所有子树当成一个大子树，这样对它来说就可以像搞二叉树一样了

这时候，这个绿色的子树k对答案的贡献就是fk*(gu+gv+gu*gv+1)

讲完dp，再来谈谈wz强大的组合数解法

我们发现之前的gx=gu+gv+gu*gv+1=(gu+1)*(gx+1),这是对于二叉树的计算方法

扩展到n叉树，就是gx=(gu+1)*(gv+1)*(ga+1)*(gb+1).........

同时通过分析样例玄学发现，Σ点n的权值*gn=ans

然后这道题就做完了（wz tql %%%wz orz）

代码自己不会写，上zay大佬的ρωρ

#include <cstdio>//用c++11写的，所以有些神奇的地方qwq

typedef long long int ll;

const int maxn = ;
const int MOD = ;

template <typename T>//据大佬说1e5的读入要用getchar()优化
inline void qr(T &x) {
  char ch;
  do { ch = getchar(); } while ((ch > '') || (ch < ''));
  do { x = (x << ) + (x << ) + (ch ^ ); ch = getchar(); } while ((ch >= '') && (ch <= ''));
}

int n, T;
int MU[maxn], frog[maxn], gorf[maxn];
bool vis[maxn];

struct Edge {
  int v;
  Edge *nxt;

  Edge(const int _v, Edge *h) : v(_v), nxt(h) {}
};
Edge *hd[maxn];

void dfs(const int u);

int main() {
  freopen("dzy.in", "r", stdin);
  freopen("dzy.out", "w", stdout);
  qr(n); qr(T);
  if (T) {
    for (int i = ; i <= n; ++i) {
      MU[i] = i;
    }
  } else {
    for (int i = ; i <= n; ++i) {
      MU[i] = ;
    }
  }
  for (int i = , u, v; i < n; ++i) {
    u = v = ; qr(u); qr(v);
    hd[u] = new Edge(v, hd[u]);
    hd[v] = new Edge(u, hd[v]);
  }
  dfs();
  printf("%d\n", frog[] % MOD);
  return ;
}

void dfs(const int u) {
  vis[u] = true;//下面开始auto(c++11)(蒟蒻的电脑c++版本过低)
  for (auto e = hd[u]; e; e = e->nxt) if (!vis[e->v]) {
    int v = e->v;
    dfs(v);
    frog[u] = (frog[u] * (gorf[v] + 1ll) % MOD) + (frog[v] * (gorf[u] + 1ll) % MOD);//frog就是前面的f
    gorf[u] = (gorf[u] + gorf[v] + (1ll * gorf[u] * gorf[v])) % MOD;//gorf就是g
  }
  frog[u] = (frog[u] + MU[u]) % MOD;
  ++gorf[u];
}

T3：锦鲤抄(洛谷P5008)

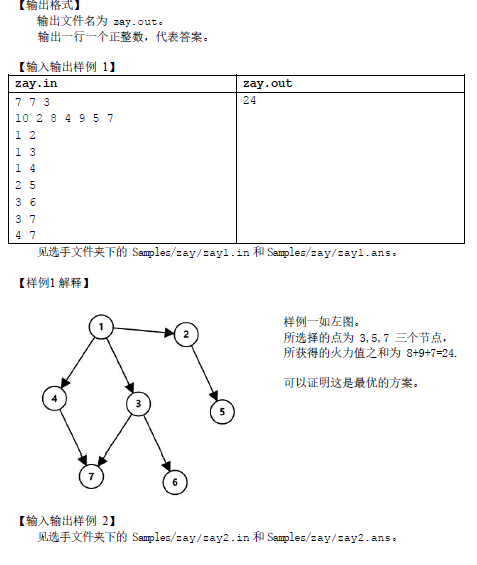
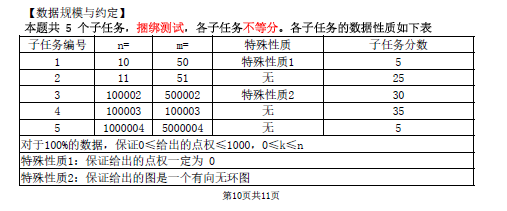
zayの题解：

这道题依旧有小数据

据说小数据是用来搜索骗分的。这道题爆搜怎么搜呢？

我们可以枚举去掉点的顺序，看是否合法，并且在合法的情况中选择最大的那个情况。

这个题中，子任务3的特殊性质是图是一个DAG。（这种特殊性质一般是让你推正解的）

在一个DAG里面，入度不为0的点总是可以被选到，也就是将所有点的点权按从大到小排序后，选出前k个点的选择顺序一定存在。（证明的话，可以找几个DAG选一选）这样子任务3就解决了。（蒟蒻写着写着就RE了）

我们从DAG中推一下正解。因为其他的数据不保证没有环，所以排序选出前k个点就不一定适用了。因为可能选着选着就会选中一个入度为0的点（选完点后要把出边删掉）。那我们可不可以把一个环看做一个巨大的点，然后使整个图形成一个DAG?当然可以（这也是正解）。于是这个题做完了。

蒟蒻不会写代码，只好拿zay的了

#include <cstdio>
#include <algorithm>
#include <functional>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif

typedef long long int ll;

namespace IPT {//读入优化
  const int L = ;
  char buf[L], *front=buf, *end=buf;
  char GetChar() {
    if (front == end) {
      end = buf + fread(front = buf, , L, stdin);
      if (front == end) return -;
    }
    return *(front++);
  }
}

template <typename T>//这个题的数据是1e7左右，要用fread,不然读入完时间就到了
inline void qr(T &x) {
  char ch = IPT::GetChar(), lst = ' ';
  while ((ch > '') || (ch < '')) lst = ch, ch=IPT::GetChar();
  while ((ch >= '') && (ch <= '')) x = (x << ) + (x << ) + (ch ^ ), ch = IPT::GetChar();
  if (lst == '-') x = -x;
}

const int maxn = ;

struct Edge {
  int v;
  Edge *nxt;

  Edge(const int _v, Edge *h) : v(_v), nxt(h) {}
};
Edge *hd[maxn];

int n, m, k, vistime, top, scnt;
int MU[maxn], dfn[maxn], low[maxn], stack[maxn], belong[maxn], minv[maxn];//belong统计缩点后每个点的入度（有时候是一个大环的入度）
bool instack[maxn], haveind[maxn];

void tarjan(const int u);

int main() {
  freopen("zay.in", "r", stdin);
  freopen("zay.out", "w", stdout);
  qr(n); qr(m); qr(k); MU[] = ;
  for (int i = ; i <= n; ++i) qr(MU[i]);//读入点权
  for (int i = , u, v; i <= m; ++i) {
    u = v = ; qr(u); qr(v);
    hd[u] = new Edge(v, hd[u]);
  }
  for (int i = ; i <= n; ++i) if (!dfn[i]) {
    tarjan(i);//缩点，我们待会再扯
  }
  for (int u = ; u <= n; ++u) {
    for (auto e = hd[u]; e; e = e->nxt) if (belong[u] != belong[e->v]) //e->nxt就是找下一条边，如果两个环的入度不相等，就满足排序取前k个点的思路是对的
{
      haveind[belong[e->v]] = true;//e->v就是e这条边的终点v
    }
  }
  for (int i = ; i <= scnt; ++i) if (!haveind[i]) {
    MU[minv[i]] = ;
  }
  std::nth_element(MU + , MU +  + k, MU +  + n,//这里是排序（取前k个的写法，也可以sort,不过这个比sort省时间） std::greater<int>());
  int ans = ;
  for (int i = ; i <= k; ++i) {
    ans += MU[i];
  }
  printf("%d\n", ans);
  return ;
}

void tarjan(const int u) {//缩点
  dfn[u] = low[u] = ++vistime;
  instack[stack[++top] = u] = true;
  for (auto e = hd[u]; e; e = e->nxt) {
    int v = e->v;
    if (!dfn[v]) {
      tarjan(v);
      low[u] = std::min(low[u], low[v]);
    } else if (instack[v]) {
      low[u] = std::min(low[u], dfn[v]);
    }
  }
  if (dfn[u] == low[u]) {
    int v, &_mv = minv[++scnt];
    do {
      instack[v = stack[top--]] = false;
      belong[v] = scnt;
      if (MU[v] < MU[_mv]) _mv = v;
    } while (v != u);
  }
}

我们扯一下缩点（Tarjan）

我们先来看一棵十分强大的dfs树（dfs树就是在有向图上，从一个点开始dfs，最终遍历的所有点和边可以构成一棵树，这棵树就是dfs树）

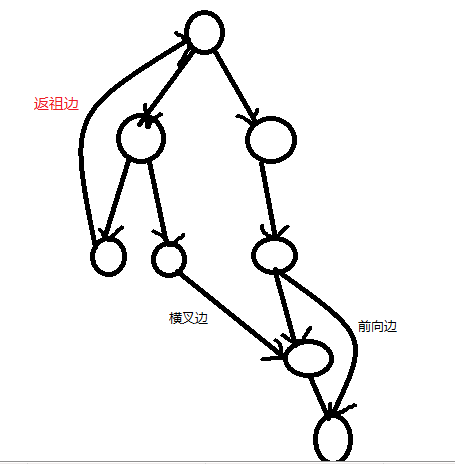
就像上图，从子孙节点指向祖宗节点的边叫返祖边，从一个节点指向兄弟节点的儿子的边叫横叉边，从祖宗节点指向孙子节点的边叫前向边

显然，这三种边中，只有返祖边会形成环，所以我们只要管返祖边就好了。

每个点不好表示，我们可以先给在dfs树上的节点一个编号，保证先遍历到的点的编号小。dfs[n]就是节点n的编号。

我们的目的是找出返祖边，并且把形成环的这一部分弄成一个大点。所以我们再建立一个数组low,low[i]指从i点能够遍历到的在dfs树上最靠上的点的编号（也就是最祖宗的点的编号）

for example(点内的数字是点的编号)

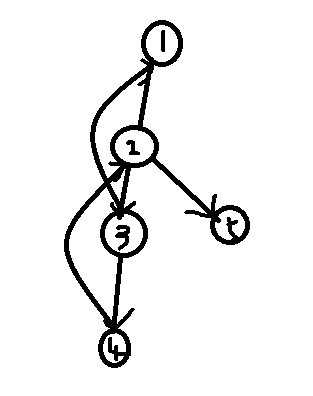
low[4]=1，因为4可以返回到2,2遍历到3,3返回到1

通过low，就可以找到返祖边，进而缩成一个点

程序实现：

将未dfs过的点进行dfs,形成dfs树，并且把遍历到的点入栈，遍历点的出边。low[i]初始化为i。如果有点的出边的终点是之前dfs过的点，则弹栈，一直弹到终点（把终点弹出），将中间所有弹出的点的low设置为终点，并将点权加和。

代码（from zay）

void tarjan(const int u) {//其实就是上面那段代码的最后一部分辣
  dfn[u] = low[u] = ++vistime;
  instack[stack[++top] = u] = true;//标记是否在栈里面
  for (auto e = hd[u]; e; e = e->nxt) {
    int v = e->v;
    if (!dfn[v]) {
      tarjan(v);
      low[u] = std::min(low[u], low[v]);//这里考虑到v可能会有返祖边，所以取min
    } else if (instack[v]) {
      low[u] = std::min(low[u], dfn[v]);//不确保u的返祖边指向的节点比v低
    }
  }
  if (dfn[u] == low[u]) {//如果没有形成环，就不缩点
    int v, &_mv = minv[++scnt];
    do {
      instack[v = stack[top--]] = false;
      belong[v] = scnt;
      if (MU[v] < MU[_mv]) _mv = v;
    } while (v != u);//也可以直接写while循环
  }
}

我们再扯点骗分技巧

1.读入优化：

1e3（读入量）及以下：scanf

1e6：getchar，也就是普通的快读

1e7:fread，一个函数，读入整个文件（以字符串的形式）。再手动计算每个数。如果令fread一次只读一个字符，那就成slow slow read了

1e8:骂出题人好了

2.暴力：

暴力主要是搜索和模拟

模拟适用于有关数据结构方面的问题

搜索用的比较多。（在数据随机时跑的贼快）搜索的状态设计一般是当前选到了第几个（在给一些东西，一个选k个的题里面），一旦超过k,就check

3.特别提示：

一般有特殊性质（不是特判送分的特殊性质）时，就是让你通过特殊性质推出正解

墙裂建议大家阅读《骗分导论》