.Net魔兽登录页面

一，页面部分展示

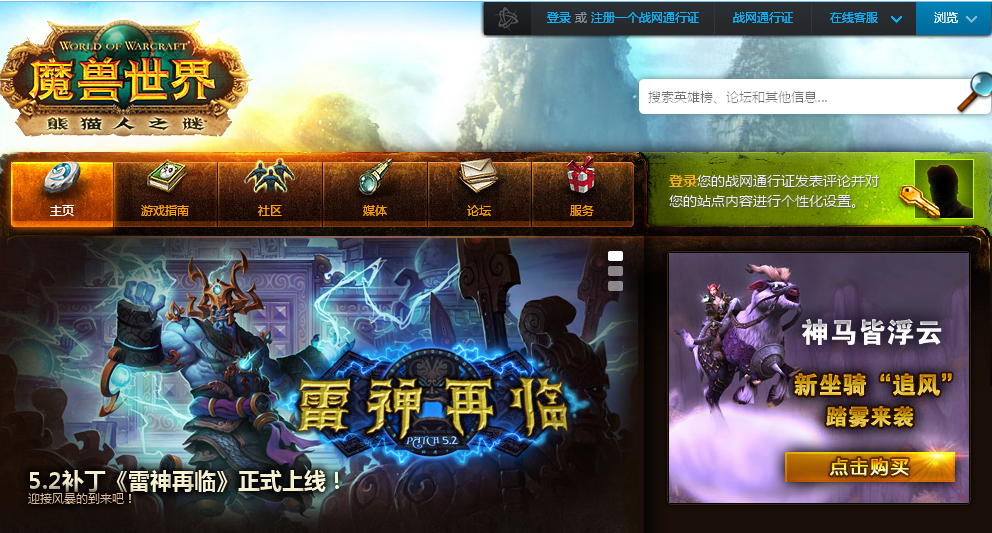
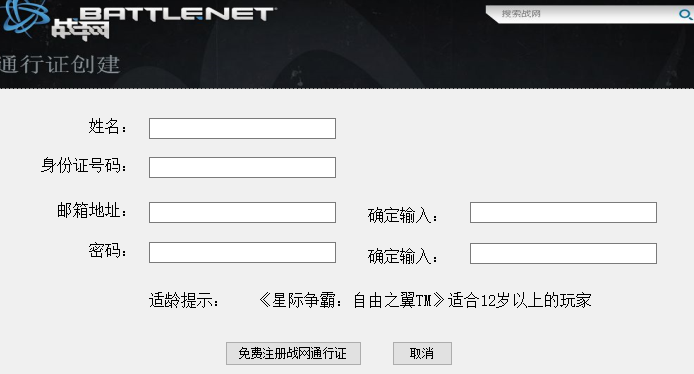
二.代码展示

1.登录页面：

public partial class FrmLogin : Form
    {
        public FrmLogin()
        {
            InitializeComponent();

        }

        private void button1_Click(object sender, EventArgs e)
        {
            if (textBox1.Text.Trim() == "" || textBox2.Text.Trim() == "")
            {
                MessageBox.Show("用户名或密码不为空！", "提示");
            }else if(textBox1.Text==FrmRegist.name&&textBox2.Text==FrmRegist.pwd){

                FrnMain fm = new FrnMain();
                fm.Show();
                this.Hide();
            }
            else
            {
                MessageBox.Show("用户名或密码错误！", "提示");
            }
        }

        private void FrmLogin_Load(object sender, EventArgs e)
        {

        }

        private void linkLabel1_LinkClicked(object sender, LinkLabelLinkClickedEventArgs e)
        {
            FrmRegist fr = new FrmRegist();

            fr.Show();
            this.Hide();
        }

　　2.注册页面：

public partial class FrmRegist : Form
    {
        public static string name;
        public static string pwd;
        public static string name2;
        public FrmRegist()
        {
            InitializeComponent();
        }

        private void pictureBox1_Click(object sender, EventArgs e)
        {

        }

        private void button1_Click(object sender, EventArgs e)
        {

            if (textBox3.Text == textBox5.Text && textBox4.Text == textBox6.Text && textBox3.Text != "" && textBox4.Text != "" && textBox5.Text != "" && textBox6.Text != "")
            {
                name = textBox3.Text;
                pwd = textBox4.Text;
                name2 = textBox1.Text;
                MessageBox.Show("注册成功！");
                FrmLogin fm = new FrmLogin();
                fm.Show();
                this.Hide();
            }
            else
            {
                MessageBox.Show("注册失败");
            }
        }

　　3.主页面：

public partial class FrnMain : Form
    {
        public FrnMain()
        {
            InitializeComponent();
        }
        public FrmLogin f1;
        private void FrnMain_Load(object sender, EventArgs e)
        {
            lblname.Text = FrmRegist.name2;
        }
    }