ISOMAP

转载 https://blog.csdn.net/dark_scope/article/details/53229427#

维度打击，机器学习中的降维算法：ISOMAP & MDS

降维是机器学习中很有意思的一部分，很多时候它是无监督的，能够更好地刻画数据，对模型效果提升也有帮助，同时在数据可视化中也有着举足轻重的作用。

一说到降维，大家第一反应总是PCA，基本上每一本讲机器学习的书都会提到PCA，而除此之外其实还有很多很有意思的降维算法，其中就包括isomap，以及isomap中用到的MDS。

ISOMAP是‘流形学习’中的一个经典算法，流形学习贡献了很多降维算法，其中一些与很多机器学习算法也有结合，但上学的时候还看了蛮多的机器学习的书，从来没听说过流形学习的概念，还是在最新的周志华版的《机器学习》里才看到,很有意思，记录分享一下。

流形学习

流形学习应该算是个大课题了，它的基本思想就是在高维空间中发现低维结构。比如这个图：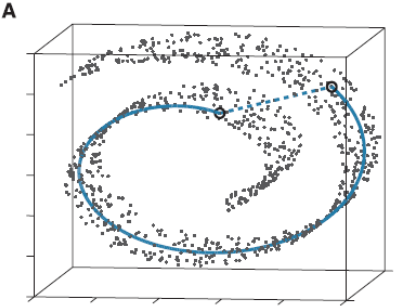 
这些点都处于一个三维空间里，但我们人一看就知道它像一块卷起来的布，图中圈出来的两个点更合理的距离是A中蓝色实线标注的距离，而不是两个点之间的欧式距离（A中蓝色虚线）。

此时如果你要用PCA降维的话，它根本无法发现这样卷曲的结构（因为PCA是典型的线性降维，而图示的结构显然是非线性的），最后的降维结果就会一团乱麻，没法很好的反映点之间的关系。而流形学习在这样的场景就会有很好的效果。

我对流形学习本身也不太熟悉，还是直接说算法吧。

ISOMAP

在降维算法中，一种方式是提供点的坐标进行降维，如PCA；另一种方式是提供点之间的距离矩阵，ISOMAP中用到的MDS(Multidimensional Scaling)就是这样。 
在计算距离的时候，最简单的方式自然是计算坐标之间的欧氏距离，但ISOMAP对此进行了改进，就像上面图示一样：

1.通过kNN(k-Nearest Neighbor)找到点的k个最近邻，将它们连接起来构造一张图。 
2.通过计算同中各点之间的最短路径，作为点之间的距离dijdij放入距离矩阵DD 
3.将DD传给经典的MDS算法，得到降维后的结果。

ISOMAP本身的核心就在构造点之间的距离，初看时不由得为其拍案叫绝，类似的思想在很多降维算法中都能看到，比如能将超高维数据进行降维可视化的t-SNE。 
ISOMAP效果，可以看到选取的最短路径比较好地还原了期望的蓝色实线，用这个数据进行降维会使流形得以保持：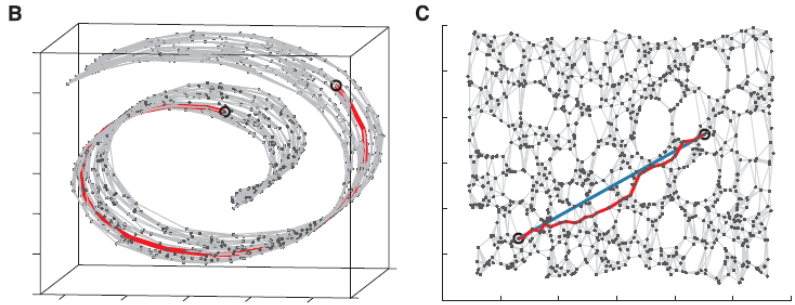 
 
ISOMAP算法步骤可谓清晰明了，所以本文主要着重讲它中间用到的MDS算法，也是很有意思的。

经典MDS（Multidimensional Scaling）

如上文所述，MDS接收的输入是一个距离矩阵DD,我们把一些点画在坐标系里： 
 
如果只告诉一个人这些点之间的距离（假设是欧氏距离），他会丢失那些信息呢？ 
a.我们对点做平移，点之间的距离是不变的。 
b.我们对点做旋转、翻转，点之间的距离是不变的。

所以想要从DD还原到原始数据XX是不可能的，因为只给了距离信息之后本身就丢掉了很多东西，不过不必担心，即使这样我们也可以对数据进行降维。

我们不妨假设：XX是一个n×qn×q的矩阵，n为样本数，q是原始的维度 
计算一个很重要的矩阵BB：

 

B=XXT    (n×n)=(XM)(XM)T    (M是一组正交基)=XMMTX=XXTB=XXT    (n×n)=(XM)(XM)T    (M是一组正交基)=XMMTX=XXT

可以看到我们通过MM对XX做正交变换并不会影响BB的值，而正交变换刚好就是对数据做旋转、翻转操作的。 
所以如果我们想通过BB反算出XX，肯定是没法得到真正的XX,而是它的任意一种正交变换后的结果。

B中每个元素的值为：

 

bij=∑k=1qxikxjkbij=∑k=1qxikxjk

计算距离矩阵DD，其中每个元素值为:

 

d2ij=(xi−xj)2=∑k=1q(xik−xjk)2=∑k=1qx2ik+x2jk−2xikxjk=bii+bjj−2bijdij2=(xi−xj)2=∑k=1q(xik−xjk)2=∑k=1qxik2+xjk2−2xikxjk=bii+bjj−2bij

\tag{dij_square}\label{dij_square} 
这时候我们有的只有DD，如果能通过DD计算出BB，再由BB计算出XX，不就达到效果了吗。

所以思路是：从D->B->X 
此时我们要对X加一些限制，前面说过我们平移所有点是不会对距离矩阵造成影响的，所以我们就把数据的中心点平移到原点，对X做如下限制（去中心化）：

 

∑i=1nxik=0,for all k=1..q∑i=1nxik=0,for all k=1..q

所以有

 

∑j=1nbij=∑j=1n∑k=1qxikxjk=∑k=1qxik(∑j=1nxjk)=0∑j=1nbij=∑j=1n∑k=1qxikxjk=∑k=1qxik(∑j=1nxjk)=0

类似的

 

∑i=1nbij=∑i=1n∑k=1qxikxjk=∑k=1qxjk(∑i=1nxik)=0∑i=1nbij=∑i=1n∑k=1qxikxjk=∑k=1qxjk(∑i=1nxik)=0

可以看到即BB的任意行(row)之和以及任意列(column)之和都为0了。

设T为BB的trace，则有：

 

∑i=1nd2ij=∑i=1nbii+bjj−2bij=T+nbjj+0∑i=1ndij2=∑i=1nbii+bjj−2bij=T+nbjj+0

 

∑j=1nd2ij=∑j=1nbii+bjj−2bij=nbii+T+0∑j=1ndij2=∑j=1nbii+bjj−2bij=nbii+T+0

 

∑i=1n∑j=1nd2ij=2nT∑i=1n∑j=1ndij2=2nT

得到B：根据公式 (???)(???)我们有：

 

bij=−12(d2ij−bii−bjj)bij=−12(dij2−bii−bjj)

而（根据前面算∑ni=1d2ij∑i=1ndij2,∑nj=1d2ij∑j=1ndij2和∑ni=1∑nj=1d2ij∑i=1n∑j=1ndij2的公式可以得到）

 

biibjj2Tn=Tn+1n∑j=1nd2ij=Tn+1n∑i=1nd2ij=1n2∑i=1n∑j=1nd2ijbii=Tn+1n∑j=1ndij2bjj=Tn+1n∑i=1ndij22Tn=1n2∑i=1n∑j=1ndij2

所以

 

bij=−12(d2ij−bii−bjj)=−12(d2ij−1n∑j=1nd2ij−1n∑i=1nd2ij+2Tn)=−12(d2ij−1n∑j=1nd2ij−1n∑i=1nd2ij+1n2∑i=1n∑j=1nd2ij)=−12(d2ij−d2i⋅−d2⋅j+d2⋅⋅)bij=−12(dij2−bii−bjj)=−12(dij2−1n∑j=1ndij2−1n∑i=1ndij2+2Tn)=−12(dij2−1n∑j=1ndij2−1n∑i=1ndij2+1n2∑i=1n∑j=1ndij2)=−12(dij2−di⋅2−d⋅j2+d⋅⋅2)

可以看到d2i⋅di⋅2 是D2D2行均值；d2⋅jd⋅j2是列均值；d2⋅⋅d⋅⋅2 是矩阵的均值。

这样我们就可以通过矩阵DD得到矩阵BB了

因为B是对称的矩阵，所以可以通过特征分解得到：

 

B=VΛV−1=VΛVTB=VΛV−1=VΛVT

在最开始我们其实做了一个假设，即DD是由一个n×qn×q的数据XX生成的，如果事实是这样的，DD会是一个对称实矩阵，此时得到的BB刚好会有qq个非0的特征值，也就是说BB的秩等于qq，如果我们想还原XX，就选择前qq个特征值和特征向量；如果想要达到降维的目的，就选择制定的pp个(p<qp<q)。

此时我们选择前pp个特征值和特征向量，（这一步和PCA里面很类似）：

 

B∗=V∗Λ∗V∗TV∗(n×p),Λ∗(p×p)B∗=V∗Λ∗V∗TV∗(n×p),Λ∗(p×p)

所以有（ΛΛ是特征值组成的对角矩阵）：

 

B∗=V∗Λ∗12∗Λ∗12V∗T=X∗X∗TB∗=V∗Λ∗12∗Λ∗12V∗T=X∗X∗T

因此

 

X∗=V∗Λ∗12X∗=V∗Λ∗12

如果选择p=qp=q的话，此时得到的X∗X∗就是原数据去中心化并做了某种正交变换后的值了。

MDS的例子

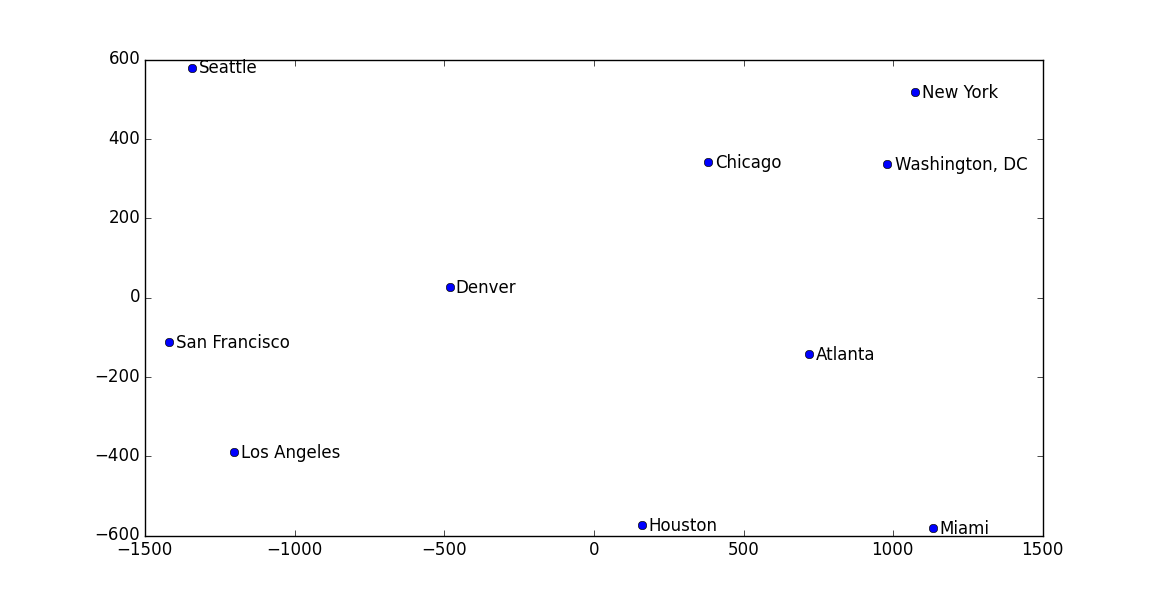
举个例子：拿美国一些大城市之间的距离作为矩阵传进去，简单写一写代码： 

import numpy as np
import matplotlib.pyplot as plt

def mds(D,q):
    D = np.asarray(D)
    DSquare = D**2
    totalMean = np.mean(DSquare)
    columnMean = np.mean(DSquare, axis = 0)
    rowMean = np.mean(DSquare, axis = 1)
    B = np.zeros(DSquare.shape)
    for i in range(B.shape[0]):
        for j in range(B.shape[1]):
            B[i][j] = -0.5*(DSquare[i][j] - rowMean[i] - columnMean[j]+totalMean)
    eigVal,eigVec = np.linalg.eig(B)
    X = np.dot(eigVec[:,:q],np.sqrt(np.diag(eigVal[:q])))

    return X

D = [[0,587,1212,701,1936,604,748,2139,2182,543],
[587,0,920,940,1745,1188,713,1858,1737,597],
[1212,920,0,879,831,1726,1631,949,1021,1494],
[701,940,879,0,1374,968,1420,1645,1891,1220],
[1936,1745,831,1374,0,2339,2451,347,959,2300],
[604,1188,1726,968,2339,0,1092,2594,2734,923],
[748,713,1631,1420,2451,1092,0,2571,2408,205],
[2139,1858,949,1645,347,2594,2571,0,678,2442],
[2182,1737,1021,1891,959,2734,2408,678,0,2329],
[543,597,1494,1220,2300,923,205,2442,2329,0]]

label = ['Atlanta','Chicago','Denver','Houston','Los Angeles','Miami','New York','San Francisco','Seattle','Washington, DC']
X = mds(D,2)
plt.plot(X[:,0],X[:,1],'o')
for i in range(X.shape[0]):
    plt.text(X[i,0]+25,X[i,1]-15,label[i])
plt.show()

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36

最后画出来的图中，各个城市的位置和真实世界中的相对位置都差不多: 

注意，这个例子中其实也有‘流形’在里面，因为我们的地球其实是一个三维，而城市间距离刻画的是在球面上的距离，所以最后如果你去看求出来的特征值，并不像前面说的那样只有q个非0的值。

reference

1. 一个nthu的课程，除了pdf还有视频，本文绝大多数关于MDS的内容都是从这里整理的：http://101.96.10.65/www.stat.nthu.edu.tw/~swcheng/Teaching/stat5191/lecture/06_MDS.pdf
2. 一个MDS的例子，用于数据可视化，例子的数据来源于这里。http://www.benfrederickson.com/multidimensional-scaling/
3. 周志华《机器学习》