【机器学习】--主成分分析PCA降维从初识到应用

一、前述

主成分分析（Principal Component Analysis，PCA）， 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

二、概念

协方差是衡量两个变量同时变化的变化程度。PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

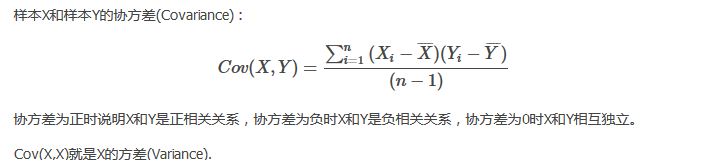
协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增，另一个也增；小于0表示一个增，一个减。如果ｘ和ｙ是统计独立的，那么二者之间的协方差就是０；但是协方差是０，并不能说明ｘ和ｙ是独立的。协方差绝对值越大，两者对彼此的影响越大，反之越小。协方差是没有单位的量，因此，如果同样的两个变量所采用的量纲发生变化，它们的协方差也会产生树枝上的变化。

协方差矩阵：

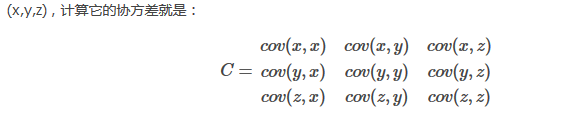
三、过程和举例

1.特征中心化。即每一维的数据都减去该维的均值。这里的“维”指的就是一个特征（或属性），变换之后每一维的均值都变成了0。

现在假设有一组数据如下：

2.每一列减去该列均值后，得到矩阵B，

3.求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

这里只有x和y，求解得

4.计算协方差矩阵C的特征值和特征向量，得到

上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为，这里的特征向量都归一化为单位向量。

5.将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是(-0.677873399, -0.735178656)T。

6.将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

FinalData(10*1) = DataAdjust(10*2矩阵) x 特征向量(-0.677873399, -0.735178656)T

得到的结果是

这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。原本数据是10行2列*2行1列（取最大的特征值对应的特征向量）=10行1列的数据。

可以参考：http://www.cnblogs.com/zhangchaoyang/articles/2222048.html

 四、总结

降维的目的：

1.减少预测变量的个数

2.确保这些变量是相互独立的

3.提供一个框架来解释结果

降维的方法有：主成分分析、因子分析、用户自定义复合等。

PCA（Principal Component Analysis）不仅仅是对高维数据进行降维，更重要的是经过降维去除了噪声，发现了数据中的模式。

PCA把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合，这些线性组合最大化样本方差，尽量使新的m个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。